Calculadoras para resolver sistemas de ecuaciones lineales (2x2)
En esta página proporcionamos dos calculadoras online para resolver sistemas de 2 ecuaciones lineales con 2 incógnitas (sistemas 2x2):
- La primera calculadora es para sistemas sin fracciones.
- La segunda calculadora es para sistemas con fracciones.
Para resolver sistemas 3x3, disponemos de la calculadora de la regla de Cramer.
Se incluye una breve introducción previa y algunos ejemplos de resolución de sistemas.
Nota: las calculadoras no muestran el procedimiento ya que resuelven el sistema aplicando la regla de Cramer.
Introducción
Recordad que los métodos básicos para resolver un sistema de ecuaciones son sustitución, igualación y reducción. También, tenemos el método gráfico.
La solución de un sistema son los números que deben tomar las incógnitas para que todas las ecuaciones del sistema se cumplan simultáneamente.
Ejemplo de sistema
$$ \begin{cases} x &-& y &=& 0 \\ x &+& 2y &=& 3 \end{cases}$$
El sistema tiene dos ecuaciones y las incógnitas son \(x\) e \(y\). Vamos a resolverlo rápidamente por el método de sustitución:
Despejando en la primera ecuación, se obtiene \(x = y\). Si sustituimos \(x\) por \(y\) en la segunda ecuación, obtenemos \(y +2y = 3\). La solución de esta última ecuación es \(y=1\) y, como \(x=y\), entonces \(x = 1\). Luego la solución del sistema del ejemplo es
$$ \begin{cases} x &=& 1 \\ y &=& 1 \end{cases}$$
No todos los sistemas tienen solución y algunos sistemas tienen infinitas soluciones.
Recordad que, una vez resuelto el sistema, podemos comprobar que la solución es, en efecto, solución del sistema:
Comprobación de la solución
Podemos comprobar la solución de un sistema sustituyendo en el propio sistema. Si todas las ecuaciones se cumplen, entonces la solución es correcta.
La solución del sistema del ejemplo anterior es \(x = y = 1\). Comprobamos la solución sustituyendo en el sistema:
$$ \begin{cases} 1 &-& 1 &=& 0 \ \checkmark \\ 1 &+& 2\cdot 1 &=& 3 \ \checkmark \end{cases}$$
Si, por ejemplo, consideramos \(x = y = 2\), se cumple la primera ecuación, pero no la segunda, por lo que no se trata de una solución del sistema:
$$ \begin{cases} 2 &-& 2 &=& 0 \ \checkmark \\ 1 &+& 2\cdot 2 &=& 4\neq 3 \ \times \end{cases}$$
Páginas con sistemas de ecuaciones:
- Método de sustitución
- Método de reducción
- Método de igualación
- Problemas resueltos de sistemas (1)
- Problemas resueltos de sistemas (2)
- Problemas resueltos de sistemas (3)
Calculadora: sistema 2x2 (sin fracciones)
| \(x +\) | \(y =\) | ← Ecuación 1 |
|||
| \(x +\) | \(y =\) | ← Ecuación 2 |
Nota: si alguno de los coeficientes tiene decimales, utilizad el punto en lugar de una coma y presionad el siguiente botón:
Calculadora: sistema 2x2 (con fracciones)
Nota: si alguno de los coeficientes no es una fracción, dejad el 1 del denominador.
| \(·x +\) | \(·y =\) | ← Ecuación 1 |
|||
| \(·x +\) | \(·y =\) | ← Ecuación 2 |
|||
Ejemplos de resolución de sistemas
Sistema 1: método de reducción 
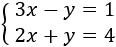
En el método de reducción se opera en las ecuaciones (si es necesario) para que desaparezca una de las incógnitas cuando se suman las ecuaciones. Se resuelve la ecuación obtenida y después se sustituye su solución en cualquiera de las ecuaciones del sistema.
Sumamos ambas ecuaciones:
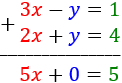
Observad que desaparece una de las incógnitas, quedando la ecuación \(5x = 5\) cuya solución es \(x = 1\).
Sustituimos \(x = 1\) en la segunda ecuación y resolvemos:
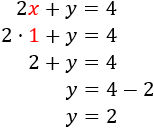
Por tanto, la solución del sistema es \(x = 1\) e \(y = 2\).
Sistema 2: método de sustitución 
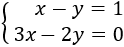
En el método de sustitución se aísla una de las incógnitas en una de las ecuaciones y se sustituye en la otra. Una vez resuelta la ecuación obtenida, se sustituye su solución para hallar la otra incógnita.
Aislamos la \(x\) en la primera ecuación:
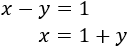
Ahora sustituimos en la segunda ecuación (en lugar de \(x\), escribimos \(1+y\)) y resolvemos:
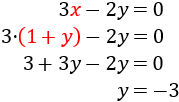
Como ya tenemos \(y = -3\), sustituimos en \( x = 1+y\) para calcular \(x\):
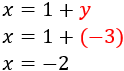
Por tanto, la solución del sistema es \(x =-2\) e \(y = -3\).
Sistema 3: método de igualación 
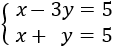
En el método de igualación, aislamos una de las incógnitas en las dos ecuaciones para igualarlas entre sí. Una vez resuelta la ecuación obtenida, se sustituye para calcular la otra incógnita.
Aislamos la \(x\) en la primera ecuación:
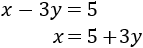
Aislamos la \(x\) en la segunda ecuación:
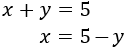
Como \(x=x\), podemos igualar ambas expresiones y resolver la ecuación:
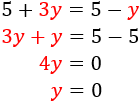
Ahora sustituimos \(y = 0\) para calcular la otra incógnita:
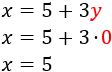
Por tanto, la solución del sistema es \(x = 5\) e \(y = 0\).

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.


