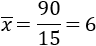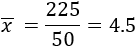Media, moda y mediana
En esta página definimos media, moda y mediana, proporcionamos algunos ejemplos y resolvemos 3 problemas.
Contenido de esta página:
- Definiciones y ejemplos
- Problemas resueltos
1. Definiciones y ejemplos
Dado un conjunto de datos \(x_1\), \(x_2\), ... , \(x_n\), la media es la suma de todos los datos dividida entre el número de datos:
$$ \bar{x} = \frac{x_1+x_2+...+x_n}{n}$$
La moda es el dato que más se repite.
Puede haber más de una moda si hay varios datos que se repiten el mismo número de veces (multimodal) y puede no haber moda si ningún dato se repite.
Ejemplo
El número de hermanos de un grupo de 5 niños es 1, 3, 0, 2 y 2.
Calculamos la media:
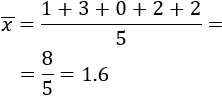
La media es 1.6 hermanos.
La moda es 2.
Para calcular la mediana, los datos deben estar ordenados (por ejemplo, de menor a mayor).
La mediana es el dato que ocupa una posición central:
- Si hay un número impar de datos, la mediana es el dato de la posición \(\frac{n+1}{2}\).
- Si hay un número par de datos, la mediana es la media de los dos datos centrales, es decir, la media de los datos de las posiciones \(n/2\) y \(n/2 +1\): $$ \frac{1}{2}\cdot \left( x_\frac{n}{2} + x_{1+\frac{n}{2}}\right) $$
Ejemplo
Las alturas (en centímetros) de los 10 alumnos de una clase son 178, 163, 155, 159, 171, 155, 172, 170, 159 y 163.
Ordenamos los datos: 155, 155, 159, 159, 163, 163, 170, 171, 172 y 178.
Como hay un número par de datos, la mediana es la media de los datos de la posición 5 y 6:
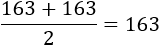
Observad que hay el mismo número de datos a uno y otro lado de la mediana (4 datos en cada lado).
Además, la media es 164.5cm y hay tres modas: 155, 159 y 163.