Contenido de esta página:
Introducción
Recordatorio: conceptos de función, dominio, codominio, imagen y gráfica.
6 Problemas resueltos sobre funciones (dominio, imagen y gráfica)
13 Problemas resueltos de planteamiento, aplicación e interpretación de funciones (lineales).
Enlaces relacionados:
Primero, recordamos los conceptos de función, dominio, codominio, imagen y gráfica. Después, resolvemos problemas sobre funciones. Los problemas están clasificados en dos grupos:
Problemas sobre los conceptos: calcular dominio, imagen, gráfica...
Problemas de aplicación: hallar expresiones de funciones e interpretar gráficas.
En esta sección repasamos los conceptos de función, dominio, codominio, imagen, anti-imagen y gráfica.
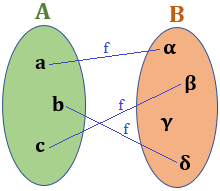
En esta colección de problemas reforzamos los conceptos relacionados con las funciones: dominio, codominio e imagen.
Problema 1
Justificar cuáles de las siguientes representaciones son la gráfica de una función y cuáles no:
Figura 1:
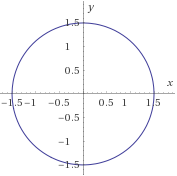
Figura 2:
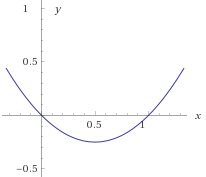
Figura 3:
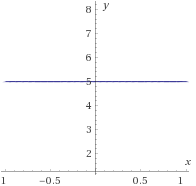
Figura 4:
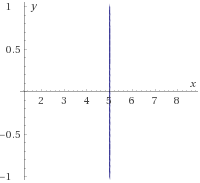
Figura 5:
Problema 2
Los dominios (los valores que puede tomar la variable) de determinadas funciones son
\( 1\leq x \leq 3 \)
\( -6\leq x < 6 \)
\( -2< x \leq 4 \)
\( -15\leq x < -5 \)
\( -6< x < 0 \)
\( -\infty < x \leq -5 \)
Se pide representarlos en la recta real.
Más información: Intervalos.
En los dos siguientes problemas, se pide representar la gráfica de una función. Para ello, puedes escribir en una tabla algunos números de su dominio y sus respectivas imágenes, obteniendo así algunos puntos de la gráfica. Después, une los puntos para obtener la gráfica.
Problema 3
Representar la gráfica de la función
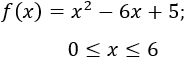
¿Cuál es el dominio y la imagen de la función?
Problema 4
Representar la gráfica de la función
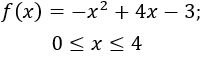
Problema 5
Calcular el dominio de las siguientes funciones.
Nota: una función puede tener varios dominios posibles, pero nosotros queremos que sea lo más grande posible.
Función \(f(x)\):
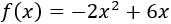
Función \(g(x)\):
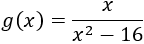
Función \(h(x)\):
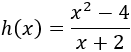
Más información: Dominio y recorrido de funciones.
Problema 6
Observando las gráficas, calcular el dominio y la imagen de las funciones que representan:
Gráfica 1:
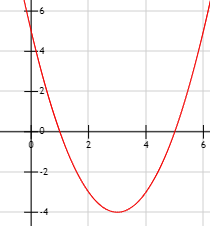
Gráfica 2:
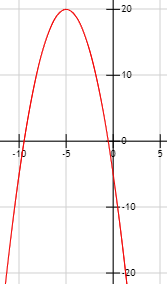
Gráfica 3:
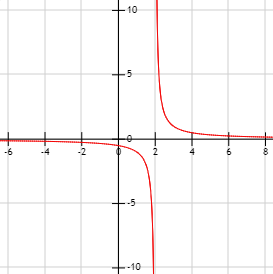
Gráfica 4:
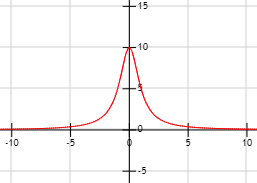
Gráfica 5:
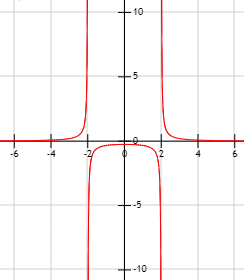
Problema 1
Si el coste de fabricación de un bolígrafo es de 0,3$ por unidad y se venden por 0,5$, calcular:
La función de beneficios en función del número de bolígrafos vendidos. Representar su gráfica.
Calcular los beneficios si se venden 5.000 bolígrafos.
Calcular cuántos bolígrafos deben venderse para generar unos beneficios de 1.648$.
Problema 2
Una empresa discográfica realiza una inversión inicial de 5.000$ para preparar las canciones de un álbum musical. El coste de fabricación y grabación de cada disco es de 4$. Además, la discográfica debe pagar al cantante 1$ por cada disco por derechos de autor.
Se decide que el precio de venta del disco sea 15$.
Se pide:
La función de beneficios (ganancias menos gastos) de la empresa en función del número de discos vendidos. Representar su gráfica.
El número de discos que deben venderse para que la empresa tenga unas ganancias de 100.000$.
¿Cuáles son los beneficios si se venden sólo 200 discos?
Problema 3
Antonio va a comprarse un teléfono móvil y está estudiando la oferta de dos compañías distintas:
La compañía A le ofrece pagar 0,2$ por el establecimiento de la llamada y 0,15$ por cada minuto de llamada.
La compañía B le ofrece pagar 0,5$ por el establecimiento de la llamada y 0,05$ por cada minuto de llamada.
Se pide:
Representar la función del coste de una llamada en cada una de las compañías.
Calcular cuándo es más recomendable una compañía u otra en función del tiempo de duración de una llamada.
Antonio sabe que, aproximadamente, realiza 100 llamadas mensuales que suman un total de 350 minutos. ¿Qué compañía le conviene?
Problema 4
Manuel quiere imprimir su novela y pide presupuesto a una papelería. Le dicen que el coste de impresión por cada libro sería:
7€ si imprime un máximo de 100 libros.
5€ si imprime una cantidad de libros superior a 100 e inferior a 300.
3€ si imprime una cantidad mínima de 300 libros.
Se pide:
Calcular la función (por partes) que proporciona el coste d impresión en función del número de libros. Representar su gráfica.
¿Cuánto debe pagar Manuel si imprime 60 libros? ¿Y si imprime 220 libros? ¿Y si imprime 400 libros?
Calcular cuánto debe pagar Manuel si imprime 299 libros. ¿Y si imprime 300 libros?. Observar la gráfica de la función para comentar el resultado.
Problema 5
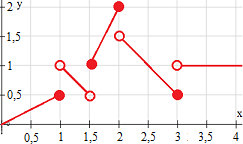
Observando la anterior gráfica de una función definida por partes, calcular:
\( f(1 ) \)
\( f(1,5 ) \)
\( f(2 ) \)
\( f(3 ) \)
\( f(4 ) \)
Problema 6
Un auto circula por una autopista recta a velocidad constante. El copiloto cuenta las farolas que hay en la calzada:
Cuando lleva 1 minuto, ha observado 3 farolas.
Cuando lleva 3 minutos, ha observado 15 farolas.
Obtener la función que proporciona el número de farolas vistas en función del tiempo sabiendo que es una ecuación lineal.
¿Cuántas farolas habrá visto en media hora?
Problema 7
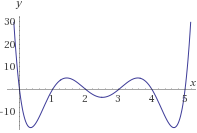
El consultor de una empresa está estudiando la función de producción de la empresa. Dicha función, \(f(x)\), proporciona el número de millares de artículos fabricados en el día \(x\) de una determinada semana.
La gráfica de la función es
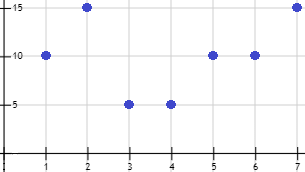
Contestar:
¿Cuál es el dominio de la función?
¿Cuál es el recorrido de la función?
¿Qué días de la semana son más productivos?
¿Qué días de la semana son menos productivos?
¿Cuántos artículos en total se han fabricado en dicha semana?
Problema 8
Se estima que en un campo de 360 naranjos producirá 30.240 mandarinas. Suponiendo que todos los árboles producen la misma cantidad de frutos, calcular:
La función que proporciona el número total de mandarinas en función del número de naranjos. ¿Qué tipo de función es? Representa su gráfica.
¿Cuántas mandarinas se producirían en total si se plantan 70 naranjos más?
¿Cuántos árboles se necesitan para producir un mínimo de 50.000 mandarinas?
Problema 9
Un laboratorio de medicinas vende una caja de penicilina que contiene 20 cápsulas por $15. Obtener:
La función \(g\) que proporciona el número de total de cápsulas vendidas en función del número de cajas vendidas.
La función \(f\) que proporciona las ganancias del laboratorio en función del número de cajas vendidas.
¿Cuántas pastillas deben venderse como mínimo para obtener una ganancia de más de $4000?
¿Cuál sería la ganancia si se venden 360 cápsulas?
Problema 10
El dueño de una tienda invirtió $18 para para comprar 60 bolsas de frituras. Si vende cada bolsa en $0,5, obtener:
La función que proporciona las ganancias con respecto del número bolsas vendidas (descontando la inversión inicial).
¿Cuántas bolsas deben venderse para recuperar la inversión?
¿Cuál es la ganancia si venden las 60 bolsas?
Problema 11
Una empresa que vende agua tiene dos máquinas embotelladoras:
La máquina 1 produce 4 lotes de 12 botellas cada 2 minutos.
La máquina 2 produce 5,5 lotes de 12 botellas cada 3 minutos.
Obtener:
La función \(f\) que proporciona el número de botellas que produce la máquina 1 en función del tiempo.
Lo mismo para la máquina 2 (función \(g\)).
Representar las gráficas de ambas funciones.
¿Qué máquina le conviene adquirir a la empresa?
Comentar el resultado relacionándolo con las gráficas.
Problema 12
Un banco tiene tres tipos de hipotecas: f, g y h. Cada una de las hipotecas tiene unos intereses distintos y los beneficios del banco en cada una de ellas vienen dadas por las funciones \(f(x)\), \(g(x)\) y \(h(x)\), respectivamente, siendo \(x\) el número de años de duración de la hipoteca.
Cuando se desea contratar una hipoteca, el banquero observa las gráficas de los beneficios para escoger la que produce más beneficios al banco:
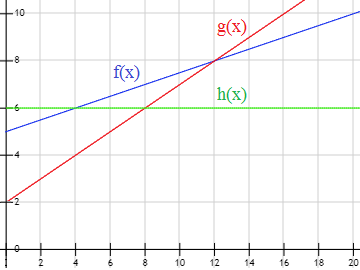
Contestar:
¿Qué hipoteca escoge el banquero si la hipoteca dura menos de 4 años?
¿Qué hipoteca escoge el banquero si la hipoteca dura exactamente 6 años?
¿Qué hipoteca escoge el banquero si la hipoteca dura más de 12 años?
Para algunas duraciones, algunas hipotecas producen los mismo beneficios. ¿Qué duraciones y qué hipotecas son?
Problema 13
El oso panda de un zoológico pesó 3,5kg al nacer. Sabiendo que los ejemplares de su especie aumentan una media de 2,5kg cada mes durante los primeros 3 años de vida, calcular:
La función que proporciona el peso del oso en función de su edad (en número de meses). Indica el dominio de la función.
Representar la gráfica de la función del apartado anterior.
Calcular, aplicando la función, el peso del oso a los 6 meses, 9 meses y 2 años de edad.
¿A qué edad el oso sobrepasará los 80kg de peso?
Problemas de funciones - (c) - matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.