Nota previa: la forma más rápida de hallar el recorrido de una función es observando su gráfica. Sin embargo, vamos a intentar deducirlo de forma razonada. Para ello, podemos ayudarnos de la monotonía (crecimiento o decrecimiento) y de límites.
Calcular el dominio y el recorrido de las siguientes funciones:
Problema 1 
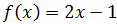
Solución:
Como se trata de una función lineal (función polinómica de grado 1), no hay ningún
punto problemático en la definición de la función, como dividir entre 0. Por tanto, el dominio es el conjunto de todos los reales:
$$ Dom(f) = \mathbb{R} $$
Recorrido
Al ser un polinomio de primer grado, el recorrido es todos los reales:
$$ Im(f)=\mathbb{R} $$
Gráfica
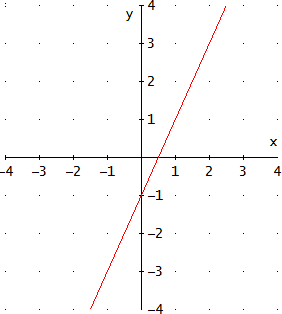
La función es una recta.
Problema 2 
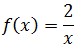
Solución:
Dominio
Como es una función racional, tenemos que excluir del dominio los puntos que
hacen que el denominador sea 0 (no podemos dividir entre 0). Por tanto, el dominio es
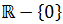
Recorrido
El recorrido es todos los reales excepto 0 ya que si suponemos que
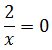
Entonces,
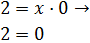
Lo cual es falso. Esto quiere decir que la ecuación no tiene solución y, por tanto,
el 0 no tiene antimagen (elemento del dominio cuya imagen es 0).
Por tanto, la imagen de \(f\) es
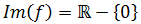
Gráfica
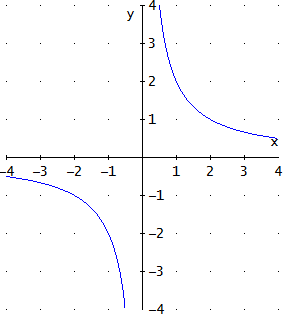
La función es una hipérbola.
Problema 3 
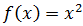
Solución:
Dominio
El dominio es todos los reales porque la función es polinómica:
$$ Dom(f) = \mathbb{R} $$
Recorrido
El recorrido es todos los reales no negativos (es decir, los positivos y 0).
Esto se debe a que la función es un cuadrado
(el cuadrado de un número es siempre positivo o cero):
$$ Im(f) = \mathbb{R}^+ \cup \{ 0\} $$
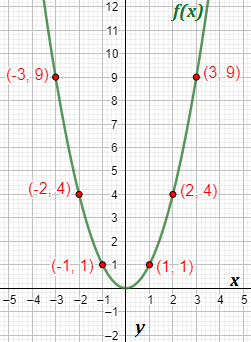
Gráfica
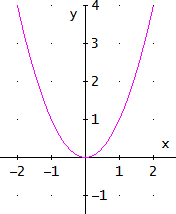
La función es una parábola.
Problema 4 
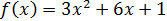
Solución:
Dominio
El dominio es todos los reales ya que la función es polinómica:
$$ Dom(f)=\mathbb{R} $$
Recorrido
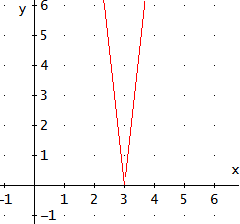
La función es una parábola (porque es un polinomio de grado 2).
El coeficiente director (el coeficiente del monomio de grado 2) es \(a=3 > 0\),
así que la parábola tiene forma de \(\cup\). Por tanto, los puntos que están por debajo del vértice
no forman parte del recorrido.
La primera coordenada del vértice de una parábola es
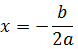
En nuestro caso,
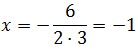
La segunda coordenada es
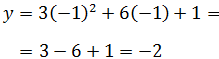
El vértice es \((-1,-2)\).
Por tanto, el recorrido de la función es
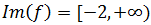
Gráfica
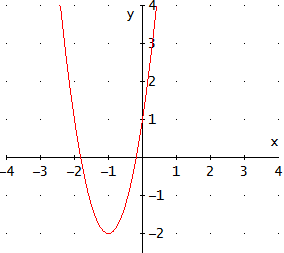
La función es una parábola.
Problema 5 
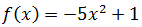
Solución:
Dominio
El dominio es todos los reales porque la función es polinómica:
$$ Dom(f) = \mathbb{R} $$
Recorrido
La función es una parábola, y como el coeficiente director
es negativo (\(a = -5\)), tiene forma de \(\cap\).
Calculamos el vértice:
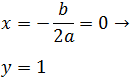
Por tanto el vértice está en el punto \((0,1)\).
Por tanto, el recorrido de la función es
![la imagen de f es (-∞ 1] imagen de la parábola](https://www.matesfacil.com/ESO/dominio/dominio5-3.png)
Gráfica
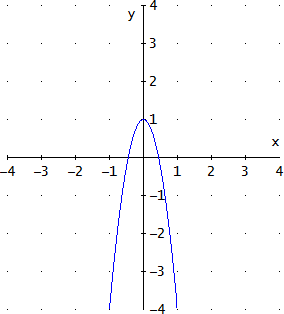
La función es una parábola.
Problema 6 
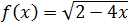
Solución:
Dominio
Como la función es una raíz cuadrada, tenemos que excluir del
dominio los puntos que hacen que el radicando sea negativo, es decir, los puntos \(x\) que verifican la inecuación
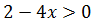
Resolvemos la inecuación:
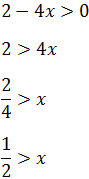
Por tanto, el dominio es
![el dominio de f es (-∞1/2] Explicamos los conceptos de dominio, codominio y recorrido (o imagen) de una función y resolvemos ejercicios. Función racional, raíz cuadrada, función definida a trozos, polinómica, exponencial, valor absoluto, logarítmica, etc. Matemáticas. Análisis de una variable real.](https://www.matesfacil.com/ESO/dominio/dominio6-3.png)
Incluimos el punto 1/2 ya que en éste el radicando es 0 y
la raíz cuadrada de 0 existe (es 0).
Recorrido
La imagen de la función es el conjunto de todos los reales no negativos. Calculamos la antiimagen de un real no negativo \(b\):
$$ b = \sqrt{2-4x}$$
$$ b^2 = 2 - 4x $$
$$ x = \frac{2-b^2}{4}$$
El recorrido de la función es
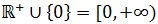
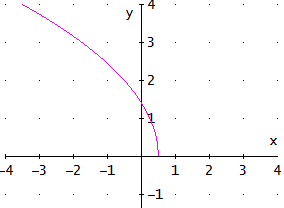
Gráfica
Problema 7 
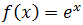
Solución:
Dominio
El dominio de la exponencial es todos los reales:
$$ Dom(f) = \mathbb{R} $$
Recorrido
Como la base de la exponencial es positiva, la imagen en siempre positiva.
Cuando \(x = 0\), la exponencial vale 1. Si \(x = -a < 0\), entonces
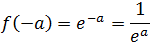
Cuanto más grande es \(a\), más grande es el denominador y, por tanto,
más pequeña es la fracción. Sin embargo, nunca será 0 ni menor que 0 (para que la
fracción sea 0 el denominador tiene que ser infinito).
La imagen de la función es
![]0,+∞) Explicamos los conceptos de dominio, codominio y recorrido (o imagen) de una función y resolvemos ejercicios. Función racional, raíz cuadrada, función definida a trozos, polinómica, exponencial, valor absoluto, logarítmica, etc. Matemáticas. Análisis de una variable real.](https://www.matesfacil.com/ESO/dominio/dominio7-2.png)
Gráfica
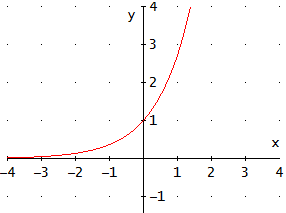
Problema 8 
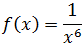
Solución:
Dominio
Como la función es racional, tenemos que exigir que
el denominador sea distinto de cero, así que tenemos que excluir el punto \(x = 0\).
El dominio es
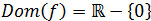
Recorrido
El numerador de la función es positivo y el denominador también lo es porque el monomio es de grado par y \(x\neq 0\). Veamos qué ocurre si suponemos que \(f(x) = 0\):
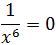
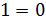
Luego \(f(x) \neq 0\).
La imagen de la función es todos los reales positivos:
$$ Im(f) = \mathbb{R}^+ $$
Todo real distinto de 0, \(b\), tiene antiimagen:
$$ f^{-1}(b) = \sqrt[6]{\frac{1}{b}} $$
Gráfica
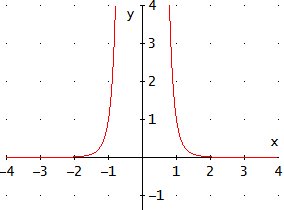
Problema 9 
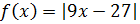
Solución:
Dominio
Recordamos que lo que hace el valor absoluto es dejar su
contenido en signo positivo. Por tanto, la función puede
reescribirse como
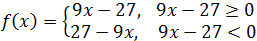
Es decir, si lo de dentro es positivo (o cero),
no cambiamos la expresión. Si lo de dentro es negativo, cambiamos su signo.
Podemos simplificar aún más resolviendo la inecuación
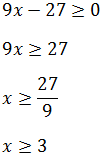
Así, la función se puede escribir como
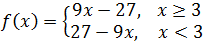
El dominio es todos los reales porque tenemos una función polinómica (a trozos).
Recorrido
En el intervalo \(x \geq 3\) la función es creciente
puesto que su coeficiente director es positivo (es 9). Luego la imagen más pequeña de la
función en este intervalo es
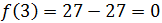
Para \(x > 3\) la función toma todos los valores positivos (porque es creciente). Es decir, el recorrido para \(x\geq 3\) son los reales no negativos.
En el intervalo \(x < 3\), la función es
decreciente (término coeficiente negativo). El valor más pequeño de
la imagen en el intervalo tiende a
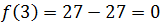
Luego en este intervalo el recorrido es todos los reales positivos.
Uniendo ambas, el recorrido de la función \(f\) es
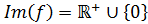
Gráfica
Problema 10 
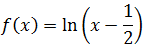
Solución:
Dominio
La base del logaritmo es \(e\) (es el logaritmo natural).
Recordad que el logaritmo natural de \(a\) es el número \(b\) tal que \(e\)
elevado a \(b\) es \(a\), es decir,
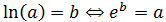
Como \(e\) es positivo, sus potencias son también positivas.
Luego el argumento debe ser positivo.
Por tanto, el dominio de la función es
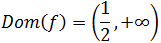
No incluimos ninguno de los extremos del intervalo (el logaritmo de 0 es infinito).
Recorrido
Cualquier real, \(b\), tiene antitimagen:
$$ f^{-1}(b) = \frac{1}{2} + e^b $$
Por tanto, el recorrido de \(f\) es el conjunto de los reales:
$$ Im(f) = \mathbb{R} $$
Gráfica
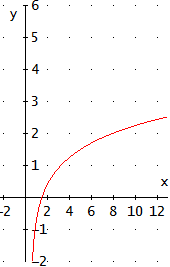
Problema 11 
![función parte entera de x, f(x) = E[x] Explicamos los conceptos de dominio, codominio y recorrido (o imagen) de una función y resolvemos ejercicios. Función racional, raíz cuadrada, función definida a trozos, polinómica, exponencial, valor absoluto, logarítmica, etc. Matemáticas. Análisis de una variable real.](https://www.matesfacil.com/ESO/dominio/dominio11.png)
Solución:
Dominio
Esta función es la parte entera de \(x\). Por ejemplo,
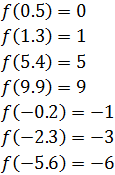
El dominio de la función es el conjutno de todos los reales:
$$ Dom(f) = \mathbb{R} $$
Recorrido
Es fácil ver que la imagen de la función es el conjunto de los números enteros:
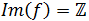
Recordad que
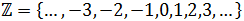
Gráfica
![gráfica de la función parte entera de x, f(x) = E[x] Explicamos los conceptos de dominio, codominio y recorrido (o imagen) de una función y resolvemos ejercicios. Función racional, raíz cuadrada, función definida a trozos, polinómica, exponencial, valor absoluto, logarítmica, etc. Matemáticas. Análisis de una variable real.](https://www.matesfacil.com/ESO/dominio/dominio11-g.png)
Problema 12 
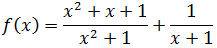
Solución:
Dominio
En un principio, como la función es una suma de fracciones,
podemos pensar que el dominio es todos los reales excepto
los puntos donde ambos denominadores se anulan. Habría que excluir los puntos \(x=0\) y (x=-1\).
Sin embargo, debemos escribir la función en su forma más
reducida posible.
Factorizamos los denominadores:
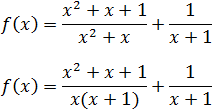
Para que ambos denominadores sean el mismo, tenemos que
multiplicar y dividir la segunda fracción por \(x\):
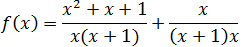
Sumamos las fracciones:
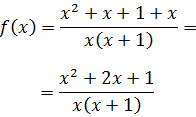
Observad que el numerador es el cuadrado de un binomio:
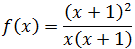
Simplificamos:
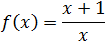
De este modo, al simplificar, vemos que sólo hay que excluir el punto \(x=0\). Así, el dominio de la función es
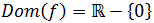
Recorrido
Para calcular el recorrido podemos escribir la función como
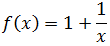
Observad que la función nunca toma el valor 1 porque el segundo sumando nunca es 0. Todos los reales no nulos sí se pueden obtener dando valores
a \(x\). Por tanto, el recorrido de la función es
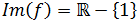
Gráfica
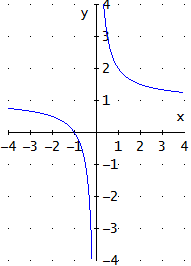
Problema 13 

Solución:
Dominio
A la hora de calcular el dominio tenemos que tener en
cuenta las siguientes consideraciones:
- las raíces deben ser no negativas
- el denominador debe ser distinto de cero
- la expresión de la función debe ser la más simplificada posible
Empezamos por el tercer punto.
Como tenemos
una diferencia de raíces cuadradas en el denominador,
multiplicamos y dividimos la función por la suma de
dichas raíces. De este modo, conseguimos que las raíces
desaparezcan:
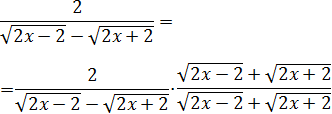
En el denominador tenemos un
producto notable: suma por diferencia igual a diferencia de cuadrados:
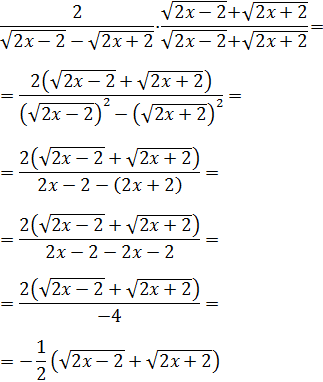
Ya no tenemos que
preocuparnos de que el denominador no sea cero.
Exigimos que los radicandos sean no negativos:
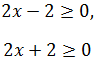
Resolvemos la primera inecuación:
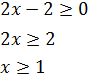
Y la segunda:
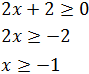
Como se tienen que cumplir ambas inecuaciones,
tenemos que exigir la solución de la primera porque es más restrictiva.
Por tanto, el dominio de la función es
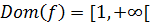
Recorrido
Encontrar el recorrido de esta función puede ser un poco
difícil.
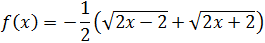
Sabemos que la función es siempre negativa porque la suma
de las raíces es positiva y ésta está multiplicada por -1/2.
Como la suma de las raíces es creciente, el coeficiente negativo hace que la función sea decreciente.
Como \(f\) es decreciente y el menor valor posible para \(x\) es 1, el valor máximo de la función es
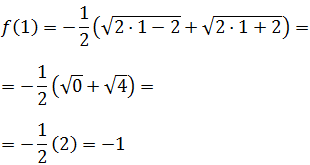
A partir de este punto, la función toma todos los valores reales menores que -1 puesto que su límite cuando \(x\to\infty\) es \(-\infty\).
Luego la imagen de la función es
![la imagen de f es (-∞, -1] Explicamos los conceptos de dominio, codominio y recorrido (o imagen) de una función y resolvemos ejercicios. Función racional, raíz cuadrada, función definida a trozos, polinómica, exponencial, valor absoluto, logarítmica, etc. Matemáticas. Análisis de una variable real.](https://www.matesfacil.com/ESO/dominio/dominio13-10.png)
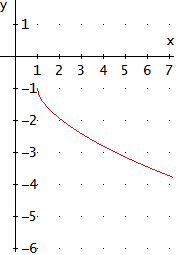
Gráfica


Dominio y recorrido de una función - © matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.


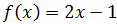

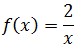
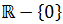
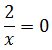
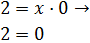
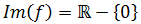

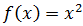

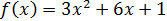
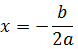
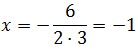
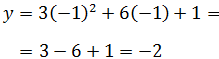
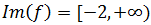

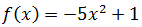
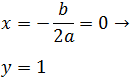
![la imagen de f es (-∞ 1] imagen de la parábola](https://www.matesfacil.com/ESO/dominio/dominio5-3.png)

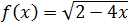
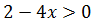
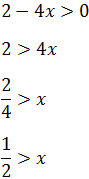
![el dominio de f es (-∞1/2] Explicamos los conceptos de dominio, codominio y recorrido (o imagen) de una función y resolvemos ejercicios. Función racional, raíz cuadrada, función definida a trozos, polinómica, exponencial, valor absoluto, logarítmica, etc. Matemáticas. Análisis de una variable real.](https://www.matesfacil.com/ESO/dominio/dominio6-3.png)
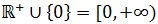

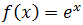
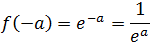
![]0,+∞) Explicamos los conceptos de dominio, codominio y recorrido (o imagen) de una función y resolvemos ejercicios. Función racional, raíz cuadrada, función definida a trozos, polinómica, exponencial, valor absoluto, logarítmica, etc. Matemáticas. Análisis de una variable real.](https://www.matesfacil.com/ESO/dominio/dominio7-2.png)

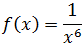
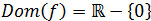
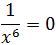
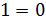


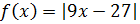
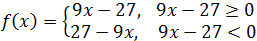
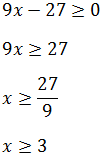
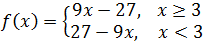
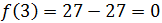
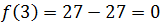
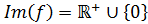

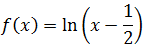
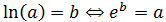
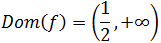

![función parte entera de x, f(x) = E[x] Explicamos los conceptos de dominio, codominio y recorrido (o imagen) de una función y resolvemos ejercicios. Función racional, raíz cuadrada, función definida a trozos, polinómica, exponencial, valor absoluto, logarítmica, etc. Matemáticas. Análisis de una variable real.](https://www.matesfacil.com/ESO/dominio/dominio11.png)
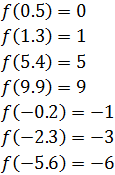
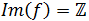
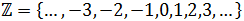
![gráfica de la función parte entera de x, f(x) = E[x] Explicamos los conceptos de dominio, codominio y recorrido (o imagen) de una función y resolvemos ejercicios. Función racional, raíz cuadrada, función definida a trozos, polinómica, exponencial, valor absoluto, logarítmica, etc. Matemáticas. Análisis de una variable real.](https://www.matesfacil.com/ESO/dominio/dominio11-g.png)
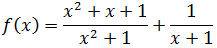
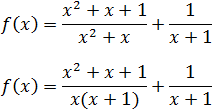
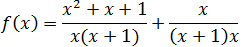
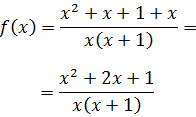
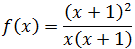
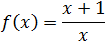
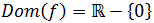
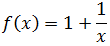
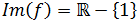


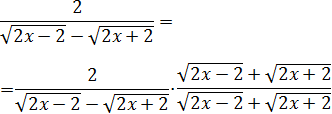
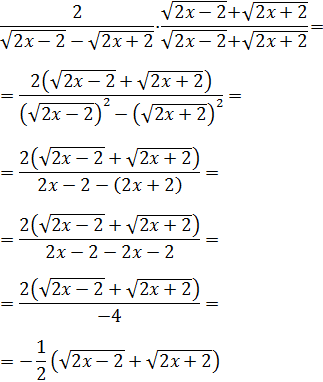
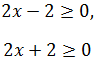
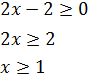
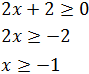
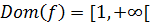
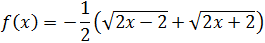
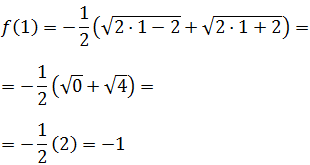
![la imagen de f es (-∞, -1] Explicamos los conceptos de dominio, codominio y recorrido (o imagen) de una función y resolvemos ejercicios. Función racional, raíz cuadrada, función definida a trozos, polinómica, exponencial, valor absoluto, logarítmica, etc. Matemáticas. Análisis de una variable real.](https://www.matesfacil.com/ESO/dominio/dominio13-10.png)



