Clasificación de los números (test)
Contenido de esta página:
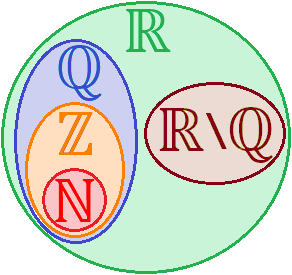
- Definición de los 5 tipos básicos de números: naturales, enteros, racionales, irracionales y reales.
- Test online (en el apartado 7).
Nota: nivel secundaria.
Nota 2: utilizaremos el símbolo "," para denotar el punto decimal. Por ejemplo, escribiremos dos coma tres como 2,3.
1. Números naturales: \(\mathbb{N}\)
El conjunto de los números naturales está formado por los números que utilizamos para contar:
1, 2, 3, 4, 5, 6...
Normalmente, el 0 no se considera como un número natural.
Los números naturales se representan con la letra manuscrita
$$\mathbb{N}$$
Es un subconjunto de los números enteros.