Calculadora de Determinante de una matriz de dimensión 2x2, 3x3 y 4x4

En esta página proporcionamos tres calculadoras online para calcular el determinante de una matriz (cada calculadora es para una dimensión: 2x2, 3x3 y 4x4). Se incluye una breve introducción previa en cada una de ellas.

Índice de calculadoras

El determinante, \(det(\cdot)\) ó \(|\cdot |\), es una función (complicada) que asigna un escalar a cada matriz \(A\) cuadrada (dimensión \(n\times n\)) de modo que cumpla determinadas propiedades (multilinealidad, antisimetría y normalidad). No obstante su complicada definición, tiene gran utilidad. Por ejemplo, nos permite saber si una matriz dada tiene o no matriz inversa, facilita la resolución de sistemas de ecuaciones lineales mediante la regla de Cramer, etc.

Existen métodos para calcular el determinante de una matriz cuadrada según su dimensión:

• Dimensión 1: el determinante de la matriz \(A = (a)\) es \(|A| = a\).
• Dimensión 2: el determinante de la matriz \(A = (a_{i,j})\) donde \(a_{i,j}\) es el elemento de la fila \(i\) y columna \(j\) es \(|A| = a_{1,1}\cdot a_{2,2} - a_{1,2}\cdot a_{2,1}\).
• Dimensión 3: usaremos la regla de Sarrus.
• Dimensión 4 o mayor: usaremos el teorema de Laplace.

Propiedades básicas del determinante

• Determinante de la matriz inversa (si existe): $$ |A^{-1}| = \frac{1}{|A|}$$
• Determinante del producto de matrices: $$ |A\cdot B| = |A|\cdot |B| $$
• Una matriz tiene inversa si y solo si su determinante es no nulo: $$\exists A^{-1} \iff |A|\neq 0 $$
• Determinante de la traspuesta: $$ |A^t| = |A|$$
• Si \(A\) tiene una fila (o columna) de ceros o una fila (o columna) que sea combinación lineal de las otras, su determinante es 0.
• Fórmula para calcular la inversa de la matriz \(A\) (a partir de su determinante y la traspuesta de su adjunta):

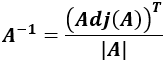
Demostraciones y más propiedades en determinante, rango y menores.

Las entradas que admiten las calculadoras son:

• Números enteros, como 2.
• Números decimales (exactos) utilizando un punto ".", como 2.345.
• Fracciones escritas con la barra "/", como 23/15.
• No se admiten números complejos, signos de operaciones o raíces y tampoco se admiten parámetros, constantes o variables.

Como la matriz \(A\) es de dimensión 2x2, tiene la forma

$$ A =\left( \begin{matrix} a & b \\ c & d \\ \end{matrix}\right)$$

El determianante de \(A\) (denotado por \(det(A)\) ó \(|A|\)) es

$$ det(A) = a·d - b·c $$

Nota: obsérvese que se multiplican los elementos en forma de ×

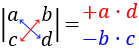
Calculadora:

\(A = \)

Calcular

Como la matriz \(A\) es de dimensión 3x3, tiene la forma

$$ A =\left( \begin{matrix} a & b & c \\ d & e & f \\ g & h & i \end{matrix}\right)$$

El determinante de \(A\) se suele calcular mediante la llamada regla de Sarrus, que es la siguiente fórmula:

$$ \begin{matrix} det(A) & = & a·e·i \\ & + & b·f·g \\ & + & d·h·c \\ & - & c·e·g \\ & - & b·d·i \\ & - & f·h·a \end{matrix} $$

Nota: puede ayudar la siguiente representación (añadimos debajo las dos primeras filas y calculamos la suma de los productos en rojo menos los productos en azul)

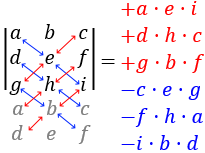
Calculadora:

\(A = \)

Calcular

Como la matriz \(A\) es de dimensión 4x4, tiene la forma

$$ A =\left( \begin{matrix} a_1 & a_2 & a_3 & a_4 \\ b_1 & b_2 & b_3 & b_4 \\ c_1 & c_2 & c_3 & c_4 \\ d_1 & d_2 & d_3 & d_4 \end{matrix}\right)$$

El determinante de una matriz de dimensión mayor que 3 suele calcularse mediante la fórmula de Laplace para determinantes. No escribimos la fórmula para no complicar la notación.

La calculadora aplica la fórmula de Laplace para desarrollar el determinante mediante la fila 1 de la matriz. La fórmula es la siguiente:

$$ det(A) = a_1·B - a_2·C + a_3·D - a_4·E $$

donde \(B\), \(C\), \(D\) y \(E\) son determinantes de submatrices de \(A\):

$$B = det \left(\begin{matrix} b_2 & b_3 & b_4 \\ c_2 & c_3 & c_4 \\ d_2 & d_3 & d_4 \end{matrix}\right) $$

$$ C = det\left(\begin{matrix} b_1 & b_3 & b_4 \\ c_1 & c_3 & c_4 \\ d_1 & d_3 & d_4 \end{matrix}\right) $$

$$ D = det\left(\begin{matrix} b_1 & b_2 & b_4 \\ c_1 & c_2 & c_4 \\ d_1 & d_2 & d_4 \end{matrix}\right) $$

$$ E = det\left(\begin{matrix} b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \\ d_1 & d_2 & d_3 \end{matrix}\right) $$

Nota: en la siguiente calculadora no mostramos los pasos por el gran número de operaciones que se realizan.

Calculadora:

\(A = \)

Calcular

Más información de la fórmula de Laplace para calcular determinantes.

---