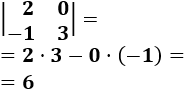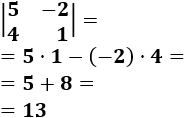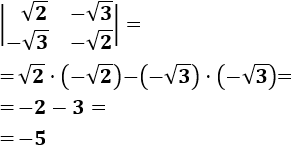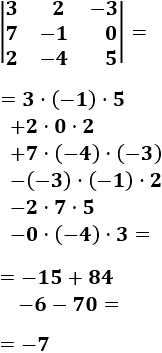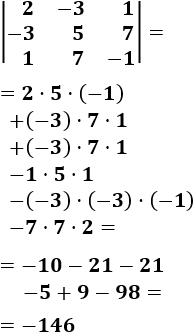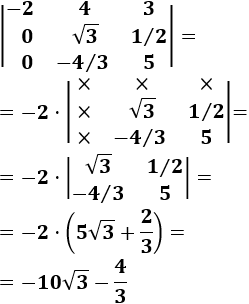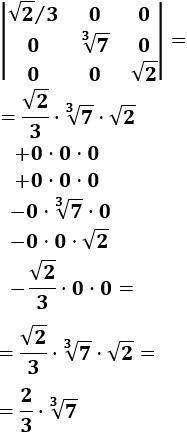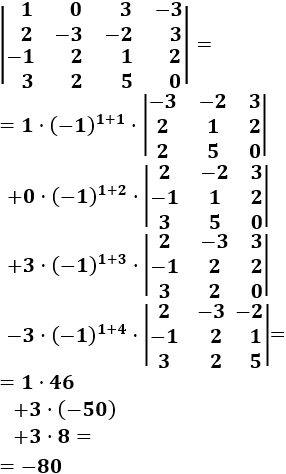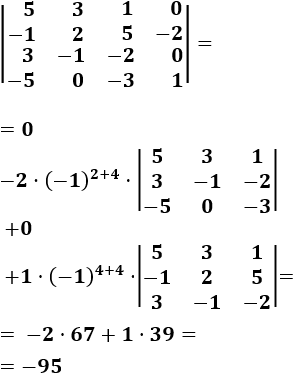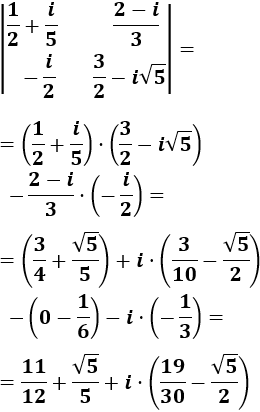Cálculo de determinantes de matrices
Contenido de esta página:
- Introducción
- Determinante de matriz 1x1
- Determinante de matriz 2x2
- Determinante de matriz 3x3
- Determinante de matriz 4x4 y superior
- Determinante de matriz diagonal
- Determinante de matriz triangular
- 10 ejemplos de determinantes de matrices de distintas dimensiones
Enlaces de interés:
Páginas relacionadas
Páginas amigas:
Introducción
La función determinante es de gran importancia en el álgebra ya que, por ejemplo, nos permite saber si una matriz es regular (si tiene matriz inversa) y, por tanto, si un sistema de ecuaciones lineales tiene solución. Además, en el caso de que el sistema de ecuaciones tenga una única solución, podemos calcularla aplicando determinantes (Regla de Cramer). Otras aplicaciones: el cálculo del producto vectorial de dos vectores y determinar si un conjunto de vectores es linealmente independiente.
Es importante que recordéis:
- Una matriz tiene inversa si y solo si su determinante es distinto de 0: $$ \exists A^{-1} \iff |A| \neq 0 $$
- Las filas de una matriz o sus columnas son linealmente dependientes si y solo si su determinante es 0.
La función determinante se define para matrices cuadradas. Su definición formal (como función multilineal alternada) es complicada, pero existen reglas y métodos para calcular los determinantes.
Denotaremos el elemento de la fila \(i\) y la columna \(j\) de la matriz \(A\) por \(a_{ij}\).
Página recomendadas:
- Calculadora online de determinantes
- Determinantes de matrices con parámetros
- Más información sobre determinantes y sus propiedades en Determinante, rango y menores de una matriz
Determinante de matriz 1x1
Dimensión 1x1
Si la dimensión de la matriz es 1, sólo tiene un elemento y su determinante es dicho elemento:
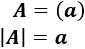
Ejemplo:
Calculamos el determinante de las matrices \(A\) y \(B\) de dimensión 1x1:
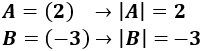
Determinante de matriz 2x2
La matriz cuadrada de dimensión 2 tiene la forma
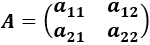
Regla: calculamos el determinante restando el producto de los elementos de las diagonales:
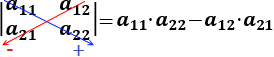
Ejemplo:
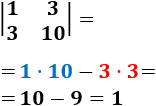
Determinante de matriz 3x3
La matriz cuadrada de dimensión 3 tiene la forma

Regla: calculamos el determinante mediante la llamada regla de Sarrus. Una forma de aplicar la regla de Sarrus es escribir las tres columnas de la matriz seguidas de la primera y la segunda columna:
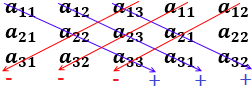
Los elementos de las diagonales con flecha hacia abajo (azul) se multiplican y se suman; los de las otras diagonales (rojo) se multiplican y se restan:

Normalmente, podemos aplicar la regla de Sarrus sin necesidad de escribir las 5 columnas, tan solo mirando la matriz. Podemos memorizar el orden de los elementos a multiplicar: primero las sumas, por diagonales, y después las restas, por diagonales también. No es tan difícil como parece.
Ejemplo:
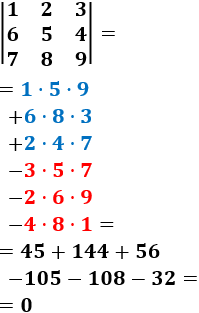
Determinante de matriz 4x4 y superior
Regla de Laplace (dimensión mayor que 3)
La regla de Laplace para calcular determinantes se puede aplicar para matrices cuadradas de cualquier dimensión, pero normalmente se hace para dimensión mayor que 3.
Hay dos versiones de la regla: desarrollo por una fila y desarrollo por una columna. El resultado es el mismo, pero escogeremos uno u otro según nos convenga.
Explicación previa del método:
- Se elige una fila \(i\) de la matriz (o una columna \(j\)).
- El determinante de la matriz es la suma de cada elemento \(a_{ij}\) de dicha fila multiplicado por \((-1)^{i+j}\) (es \(+1\) o \(-1\) según la posición del elemento) y por el determinante de la submatriz \(A_{ij}\).
Recordad que la submatriz \(A_{ij}\) es la matriz que resulta al eliminar la fila \(i\) y columna \(j\) de la matriz \(A\).
Consejo: es mejor desarrollar por la fila o la columna que tenga más ceros, ya que no tendremos que calcular el determinante cuando \(a_{ij}=0\).
Fórmula: Desarrollo por la fila \(i\) de la matriz \(A\) de dimensión \(n\):
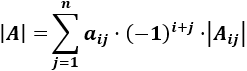
siendo \(A_{ij}\) la matriz de dimensión \(n-1\) resultante al eliminar la fila \(i\) y la columna \(j\) de \(A\).
Por tanto, si la matriz es dimensión \(n\), tendremos que calcular \(n\) determinantes de matrices de dimensión \(n-1\). Esta es la razón por la que solo usamos esta regla cuando no hay otra opción (dimensión mayor que 3).
Ejemplo 1:
Para que sea más sencillo, vamos a calcular el determinante de una matriz de dimensión 2x2 desarrollando por la fila 1:
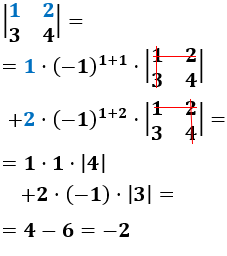
Ejemplo 2:
Vamos a calcular el determinante de una matriz de dimensión 3x3 mediante el desarrollo por la fila 1:
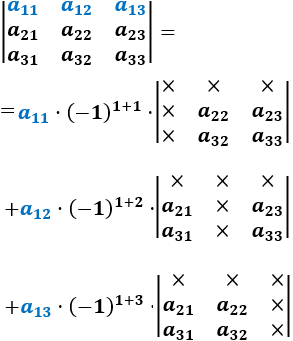
Hemos escrito el símbolo \(\times\) en las entradas de la matriz que se han eliminado, obteniendo así determinantes de matrices 2x2.
Si calculamos los determinantes anteriores obtenemos la regla de Sarrus.
Ejemplo 3:
Calcularemos el determinante de la siguiente matriz de dimensión 3:
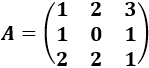
Como tenemos un 0 en la segunda fila, desarrollamos por la fila 2:
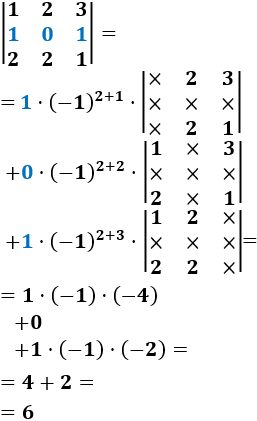
Fórmula: Desarrollo por la columna \(j\) de la matriz \(A\) de dimensión \(n\) es
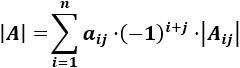
Nota: elegir la fila (o columna) con ceros no es una tontería, pues cuando estamos en dimensiones grandes, no tener que calcular un determinante ahorra mucho tiempo.
Determinante de matriz diagonal
Una matriz \(A\) cuadrada es diagonal cuando todos los elementos que no están en la diagonal son iguales a 0.
Definición: si denotamos \(a_{ij}\) al elemento de la fila \(i\) y columna \(j\) de \(A\), entonces \(A\) es diagonal cuando \(a_{ij} = 0\) para todo \(i\neq j\).
Ejemplo 1:
- La matriz identidad es diagonal:
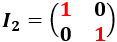
- La siguiente matriz 3x3 también es diagonal:
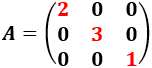
Nota: los elementos de la diagonal (esto es, los \(a_{ii}\)) también pueden ser 0.
Determinante de matriz triangular
Es importante saber que el determinante de una matriz diagonal cuadrada, sea cual sea su dimensión, es el producto de los elementos de su diagonal:
$$ |A| = \prod_{i=1}^{n} a_{ii} = a_{11}\cdot a_{22} \cdot\cdot\cdot a_{nn}$$
Ejemplo 2:
Calculamos el determinante de la matriz \(A\) del ejemplo anterior:
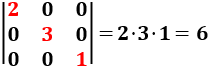
Determinante de matriz triangular
Lo mismo ocurre con las matrices triangulares: su determinante es el producto de los elementos de su diagonal.
- Una matriz es triangular superior cuando los elementos bajo su diagonal son iguales a 0. Es decir, \(a_{ij} = 0\) si \(i> j\).
- Una matriz es triangular inferior cuando los elementos sobre su diagonal son iguales a 0. Es decir, \(a_{ij} = 0\) si \(i< j\).
Ejemplo:
Calculamos el determinante de la siguiente matriz triangular:
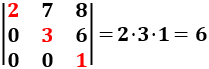
Ejemplos de cálculo de determinantes
Determinante 1
Matriz de dimensión 2x2
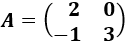
Determinante 2
Matriz de dimensión 2x2
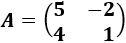
Determinante 3
Matriz de dimensión 2x2
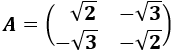
Determinante 4
Matriz de dimensión 3x3

Determinante 5
Matriz simétrica de dimensión 3x3
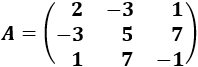
Determinante 6
Matriz de dimensión 3x3 (aplicar Laplace)
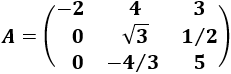
Determinante 7
Matriz diagonal de dimensión 3x3
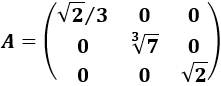
Determinante 8
Matriz de dimensión 4x4
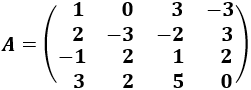
Determinante 9
Matriz de dimensión 4x4
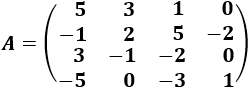
Determinante 10
Matriz de dimensión 3x3 con entradas complejas
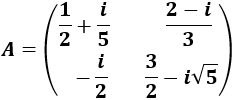
Cálculo de determinantes de matrices- © - matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.