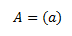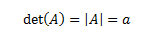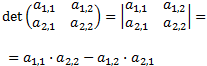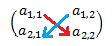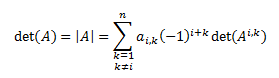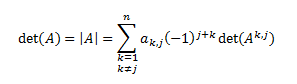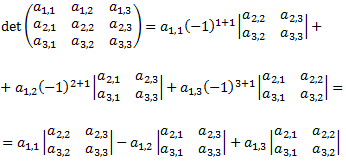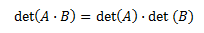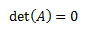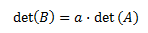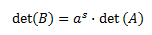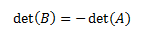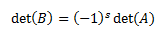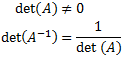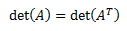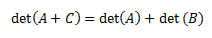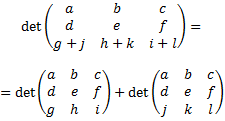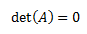logotipo matesfacil

Determinante, rango y menores

Proporcionamos las reglas para calcular el determinante de una matriz según su dimensión, enunciamos las propiedades de la función determinante, definimos el rango y los menores de una matriz y enunciamos el Teorema de Rouché-Frobenius.

Contenido de esta página:

  1. Introducción
  2. Determinante de una matriz según su dimensión
  3. Propiedades de la función determinante
  4. Rango y menores principales
  5. Teorema de Rouché-Frobenius

Problemas resueltos:

1. Introducción

La función determinante de una matriz cuadrada \(A\), \(|A|\), es una herramienta clave en el álgebra matricial. Entre otras cosas,

  • Permite determinar si la matriz es regular, es decir, si tiene matriz inversa. Esto ocurre cuando \(|A|\neq 0\). Además, si la matriz \(A\) es regular, su inversa es \(A^{-1} = Adj(A)^T/|A|\).
  • Permite conocer el número de soluciones de un sistema de ecuaciones lineales (Teorema de Rouché-Frobenius). Y si el sistema de ecuaciones tiene una única solución, podemos obtenerla calculando algunos determinantes (regla de Cramer).

La definición formal de la función determinante no es demasiado intuitiva (se basa en permutaciones). De hecho, no se utiliza a la hora de calcular el determinante de una matriz. Para ello, disponemos de varios métodos o reglas según la dimensión de la matriz.

2. Determinante de una matriz

El determinante de una matriz \(A\) sólo está definido para matrices cuadradas (mismo número de filas que de columnas). Se representa por \(det(A)\) ó \(|A|\).

Matriz de dimensión 1x1

Si \(A\) es una matriz de dimensión 1x1, tiene la forma

Reglas para calcular el determinante de una matriz según su dimensión, enunciamos las propiedades de la función determinante, definimos el rango y los menores de una matriz y enunciamos el Teorema de Rouché-Frobenius. Álgebra matricial. Matrices.

Su determinante es

Reglas para calcular el determinante de una matriz según su dimensión, enunciamos las propiedades de la función determinante, definimos el rango y los menores de una matriz y enunciamos el Teorema de Rouché-Frobenius. Álgebra matricial. Matrices.

Matriz de dimensión 2x2

Si \(A\) es una matriz de dimensión 2x2, tiene la forma

Reglas para calcular el determinante de una matriz según su dimensión, enunciamos las propiedades de la función determinante, definimos el rango y los menores de una matriz y enunciamos el Teorema de Rouché-Frobenius. Álgebra matricial. Matrices.

Su determinante es

Reglas para calcular el determinante de una matriz según su dimensión, enunciamos las propiedades de la función determinante, definimos el rango y los menores de una matriz y enunciamos el Teorema de Rouché-Frobenius. Álgebra matricial. Matrices.

Observad que se multiplican los elementos de la matriz en diagonal y se restan los resultados:

Reglas para calcular el determinante de una matriz según su dimensión, enunciamos las propiedades de la función determinante, definimos el rango y los menores de una matriz y enunciamos el Teorema de Rouché-Frobenius. Álgebra matricial. Matrices.

Ver ejemplo

Matriz de dimensión 3x3

Si \(A\) es una matriz de dimensión 3x3, tiene la forma

Reglas para calcular el determinante de una matriz según su dimensión, enunciamos las propiedades de la función determinante, definimos el rango y los menores de una matriz y enunciamos el Teorema de Rouché-Frobenius. Álgebra matricial. Matrices.

Su determinante es (Regla de Sarrus)

Reglas para calcular el determinante de una matriz según su dimensión, enunciamos las propiedades de la función determinante, definimos el rango y los menores de una matriz y enunciamos el Teorema de Rouché-Frobenius. Álgebra matricial. Matrices.

Observad que se multiplican los elementos de la matriz en diagonales: de izquierda a derecha en positivo y de derecha a izquierda en negativo.

Ver ejemplo

Más ejemplos: cálculo de determinantes.

Matriz de dimensión nxn

Cuando la matriz es de dimensión mayor que 3, aplicamos el desarrollo de Laplace (también se puede utilizar para dimensiones menores).

Sea \(A = (a_{i,j})\) una matriz de dimensión nxn, es decir, el elemento de la fila \(i\) y columna \(j\) es \(a_{i,j}\). Denotamos por \(A^{r,s}\) a la submatriz que resulta al eliminar la fila \(r\) y columna \(s\) de la matriz \(A\).

Podemos calcular el determinante de \(A\) desarrollándolo por la fila \(i\) mediante

Reglas para calcular el determinante de una matriz según su dimensión, enunciamos las propiedades de la función determinante, definimos el rango y los menores de una matriz y enunciamos el Teorema de Rouché-Frobenius. Álgebra matricial. Matrices.

O por la columna \(j\) mediante

Reglas para calcular el determinante de una matriz según su dimensión, enunciamos las propiedades de la función determinante, definimos el rango y los menores de una matriz y enunciamos el Teorema de Rouché-Frobenius. Álgebra matricial. Matrices.

Ver ejemplo

3. Propiedades de la función determinante

Todas las propiedades se pueden demostrar fácilmente aplicando el desarrollo de Laplace.

Sean \(A\) y \(B\) dos matrices cuadradas de dimensión \(n\). Entonces,

  • El determinante del producto es el producto de los determinantes:

    Reglas para calcular el determinante de una matriz según su dimensión, enunciamos las propiedades de la función determinante, definimos el rango y los menores de una matriz y enunciamos el Teorema de Rouché-Frobenius. Álgebra matricial. Matrices.

  • Si \(A\) tiene una o más filas (o columnas) nulas,

    Reglas para calcular el determinante de una matriz según su dimensión, enunciamos las propiedades de la función determinante, definimos el rango y los menores de una matriz y enunciamos el Teorema de Rouché-Frobenius. Álgebra matricial. Matrices.

  • Si \(B\) es la matriz que se obtiene al multiplicar una fila de \(A\) por por el escalar \(a\),

    Reglas para calcular el determinante de una matriz según su dimensión, enunciamos las propiedades de la función determinante, definimos el rango y los menores de una matriz y enunciamos el Teorema de Rouché-Frobenius. Álgebra matricial. Matrices.

  • Si \(B\) es la matriz que se obtiene al multiplicar \(s\) filas de \(A\) por por el escalar \(a\),

    Reglas para calcular el determinante de una matriz según su dimensión, enunciamos las propiedades de la función determinante, definimos el rango y los menores de una matriz y enunciamos el Teorema de Rouché-Frobenius. Álgebra matricial. Matrices.

  • Si \(B\) es la matriz que se obtiene al cambiar el orden a una fila (o columna) de \(A\),

    Reglas para calcular el determinante de una matriz según su dimensión, enunciamos las propiedades de la función determinante, definimos el rango y los menores de una matriz y enunciamos el Teorema de Rouché-Frobenius. Álgebra matricial. Matrices.

  • Si \(B\) es la matriz que se obtiene al cambiar el orden de \(s\) filas (o columnas) de \(A\),

    Reglas para calcular el determinante de una matriz según su dimensión, enunciamos las propiedades de la función determinante, definimos el rango y los menores de una matriz y enunciamos el Teorema de Rouché-Frobenius. Álgebra matricial. Matrices.

  • Si \(A\) es regular (tiene inversa),

    Reglas para calcular el determinante de una matriz según su dimensión, enunciamos las propiedades de la función determinante, definimos el rango y los menores de una matriz y enunciamos el Teorema de Rouché-Frobenius. Álgebra matricial. Matrices.

    De hecho, la matriz es regular si, y sólo si, su determinante es no nulo.

  • Determinante de la traspuesta:

    Reglas para calcular el determinante de una matriz según su dimensión, enunciamos las propiedades de la función determinante, definimos el rango y los menores de una matriz y enunciamos el Teorema de Rouché-Frobenius. Álgebra matricial. Matrices.

  • Sean \(B\) una matriz igual que \(A\) excepto la fila \(k\) y \(C\) una matriz nula excepto la fila \(k\), que es la misma que la fila \(k\) de \(B\). Entonces,

    Reglas para calcular el determinante de una matriz según su dimensión, enunciamos las propiedades de la función determinante, definimos el rango y los menores de una matriz y enunciamos el Teorema de Rouché-Frobenius. Álgebra matricial. Matrices.

    Por ejemplo, si las matrices son de dimensión 3,

    Reglas para calcular el determinante de una matriz según su dimensión, enunciamos las propiedades de la función determinante, definimos el rango y los menores de una matriz y enunciamos el Teorema de Rouché-Frobenius. Álgebra matricial. Matrices.

  • Si \(B\) es la matriz que resulta al sumar a una fila de \(A\) otra fila multiplicada por un escalar (operación elemental fila),

    Reglas para calcular el determinante de una matriz según su dimensión, enunciamos las propiedades de la función determinante, definimos el rango y los menores de una matriz y enunciamos el Teorema de Rouché-Frobenius. Álgebra matricial. Matrices.

  • Si \(A\) tiene dos o más filas o columnas proporcionales (filas o columnas linealmente dependientes),

    Reglas para calcular el determinante de una matriz según su dimensión, enunciamos las propiedades de la función determinante, definimos el rango y los menores de una matriz y enunciamos el Teorema de Rouché-Frobenius. Álgebra matricial. Matrices.

4. Rango y menores principales

Menor de orden \(k\)

Sea \(A\) una matriz de dimensión mxn y sea \(k\) un natural tal que \(k \leq min\{m,n\}\).

Llamamos menor de orden \(k\) al determinante de cualquier submatriz de \(A\) de dimensión kxk (hay varios menores de cada orden, excepto cuando \(k=m=n\)).

Teoremas importantes:

  • Si existe algún menor de orden \(k\) no nulo, el rango de la matriz \(A\) es mayor o igual que \(k\).
  • Si todos los menores de orden \(k\) son nulos, el rango de la matriz es estrictamente menor que \(k\).

El menor principal de orden \(k\) es el menor de orden \(k\) correspondiente a la submatriz formada por las \(k\) primeras filas y columnas de \(A\) (sólo hay un menor principal para cada \(k\)).

Rango de una matriz

Sea \(A\) una matriz (cuadrada o no), llamamos rango de \(A\) (y lo donatamos por \(r(A)\), \(rank(A)\) ó \(rango(A)\)) a cualquiera de los siguientes números:

  • Número de filas independientes.
  • Número de unos principales de la matriz en forma escalonada reducida.
  • El número de filas no nulas de la matriz en forma escalonada reducida.
  • El orden máximo de los menores no nulos.

Los números de los puntos anteriores coinciden.

Propiedades del rango

  • El rango es el mismo para matrices equivalentes.
  • El rango de una matriz cuadrada de dimensión \(n\) es \(n\) si, y sólo si, la matriz es regular.

5. Teorema de Rouché-Frobenius

El teorema de Rouché-Frobenius es uno de los más importantes del álgebra matricial, al menos en cuanto a aplicaciones prácticas, ya que nos permite clasificar un sistema de ecuaciones lineales según el rango de su matriz ampliada \(A^* = (A|b)\).

Sea A·x = b un sistema de m ecuaciones lineales con n incógnitas (sobre un cuerpo en general), siendo m y n naturales (no nulos). Entonces,

  • A·x = B es compatible si, y sólo si, rango(A) = rango (A|b).
  • A·x = b es compatible determinado si, y sólo si, rango(A) = n = rango(A|b).

Demostración del teorema y ejemplos de aplicación en Teorema de Rouché-Frobenius.




contacto

ejercicios interactivos de matemáticas


Determinante, rango y menores de una matriz - © matesfacil.com

Creative Commons License
Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.