El contenido de esta página es teórico. Contenido:
Derivable y Derivada
Derivadas elementales
Propiedades y Reglas de derivación
Regla de la cadena
Extremos y Monotonía
Teorema del Valor Medio de Lagrange
Sean \(I\) un intervalo abierto de los reales, \(a\) un punto de \(I\) y sea la función
$$ f:I\rightarrow \mathbb{R}$$
Entonces, decimos que \(f\) es derivable en el punto \(a\) si existe el siguiente límite y, en tal caso, a su valor lo denotamos por \(f'(a)\):
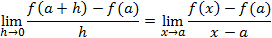
Nota: los dos límites anteriores son equivalentes.
Decimos que \(f\) es derivable en \(I\) si lo es en todos los puntos del intervalo \(I\).
Llamamos derivada de \(f\) a la función \(f'(x)\) siendo \(x\in I\).
Llamamos derivadas elementales o inmediatas a las derivadas de funciones elementales (por ejemplo, la función constante, potencia, coseno, exponencial, logaritmo, etc.).
Las funciones más complejas se pueden escribir como composición de funciones elementales. Podremos derivar estas funciones más complejas utilizando las reglas de derivación, la regla de la cadena y las derivadas elementales.
Las derivadas elementales se calculan con la propia definición de derivada (calculando el límite) y las escribimos en una tabla (Tabla (PDF) de derivadas elementales) para utilizarlas al derivar las funciones más complejas.
Veamos dos ejemplos del cálculo de derivadas a partir de su definición:
Ejemplo 1: derivada de la función constante.
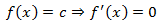
Ejemplo 2: derivada de la función seno.
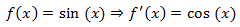
Una de las más importantes propiedades es la relación entre derivabilidad y continuidad:
Si \(f\) es derivable en el punto \(a\), entonces \(f\) es continua en \(a\).
1. Derivada de la inversa: Sea \(f\) derivable en el punto \(a\) tal que la derivada en dicho punto no se anula, esto es, \(f'(a)\neq 0\), y existe la inversa de \(f\) en un entorno de \(f(a)\), entonces
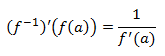
2. Derivada del producto por una constante: Sea \(f\) derivable en \(a\) y sea \(k\) una constante, entonces
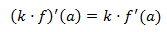
3. Derivada de la suma de dos funciones: Sean \(f\) y \(g\) dos funciones derivables en \(a\), entonces
$$ (f+g)'(a) = f'(a)+g'(a)$$
Omitimos la demostración por su inmediatez.
4. Derivada del producto de funciones: Sean \(f\) y \(g\) dos funciones derivables en \(a\), entonces,
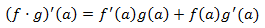
5. Derivada del cociente de funciones: Sean \(f\) y \(g\) funciones derivables en \(a\) siendo \(g(a)\neq 0\), entonces
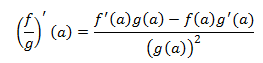
La regla de la cadena es un teorema de gran importancia por su aplicación. Este resultado es el que nos permite calcular la derivada de la composición de funciones.
Regla de la cadena: Sean \(f\) y \(g\) dos funciones tales que \(f\) es derivable en \(a\) y \(g\) es derivable en \(f(a)\), entonces
$$ (g\circ f )'(a) = g'(f(a))\cdot f'(a) $$
Veamos un sencillo ejemplo de su aplicación:
Calcular la derivada de la función \(f(x) = sin(x^2)\) con el límite de la definición de la derivada sería una tarea más o menos tediosa que podemos evitar.
La función \(f\) es composición de las funciones \(h(x) = sin(x)\) y \(g(x) = x^2\):
$$ f(x) = (h\circ g)(x) = h(g(x))$$
Las derivadas de las funciones implicadas son \(h'(x) = cos(x)\) y \(g'(x) = 2x\).
Aplicamos la regla de la cadena:
$$ f'(x) = h'(g(x))\cdot g'(x)=$$
$$= cos(x^2)\cdot 2x$$
Enlace: problemas de calcular derivadas (aplicando la regla de la cadena).
Criterio de extremos:
Si \(f\) es derivable en un extremo (máximo o mínimo local), entonces la derivada es 0 en dicho punto.
Criterio de monotonía:
Si \(f\) es derivable en \(a\):
Si \(f'(a)>0\), entonces \(f\) es creciente en un entorno de \(a\).
Si \(f'(a)< 0\), \(f\) es decreciente en un entorno de \(a\).
Si \(f'(a)=0\), decimos que \(a\) es un punto crítico, esto significa que \(a\) es un posible extremo (local).
Criterio de extremo (segunda derivada): Si \(a\) es un punto con \(f'(a)=0\) (es decir, \(a\) es un punto crítico) y \(f\) admite segunda derivada en \(a\):
Si \(f''(a)>0\), el punto \(a\) es un mínimo local.
Si \(f''(a)< 0\), el punto \(a\) es un máximo local.
Si \(f''(a)=0\), el punto \(a\) es un punto de inflexión (punto donde cambia la monotonía).
Sea la función continua \(f:[a,b]\rightarrow \mathbb{R}\) derivable en el intervalo abierto \(]a,b[\). Entonces,\(\exists c\in ]a,b[\) tal que
$$f(b)-f(a) = f'(c)(b-a)$$
Se puede demostrar aplicando el teorema de Rolle a la función
$$ f(x)-\frac{f(b)-f(a)}{b-a}(x-a)-f(a) $$
Enlaces:

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.