Problema 1
Comprobar si la función \(f(x)=x^2\) cumple las hipótesis del teorema de Rolle en el intervalo \(\left[-1,1\right]\). En caso afirmativo, hallar \(c\) del intervalo tal que \(f'(c)=0\).
Ver solución
Como la función es polinómica, es continua en \(\left[-1,1\right]\) y derivable en \(\left(-1,1\right)\).
Además, se cumple \(f(-1) = f(1)\):
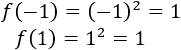
Se cumplen las hipótesis.
La derivada de la función es
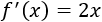
Igualamos a 0 y resolvemos:
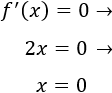
Por tanto, el único punto del intervalo donde se anula la derivada es \(x = 0\). Este punto es el número \(c\) del teorema.
Gráfica:
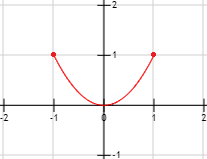
Problema 2
Comprobar si la función \(f(x) = x-3\) cumple las hipótesis del teorema de Rolle en el intervalo \(\left[0,1\right]\). En caso afirmativo, hallar \(c\) del intervalo tal que \(f’(c)=0\). En caso contrario, ¿se cumplen las hipótesis del teorema en un intervalo cerrado contenido en el anterior?
Ver solución
Por ser una función polinómica, es continua en el intervalo \(\left[0,1\right]\) y derivable en \(\left(0,1\right)\).
Pero no se cumple \(f(0) = f(1)\), por lo que no se cumplen todas las condiciones del teorema.
Respecto a la segunda pregunta, la continuidad y la derivabilidad no son el problema. El problema es que no existen \(a\) y \(b\) distintos tales que \(f(a) = f(b)\), es decir, la función es inyectiva y, por tanto, en ningún intervalo se cumplen las condiciones.
Comprobación de la inyectividad:
Supongamos que \(f(a) = f(b)\). Entonces,
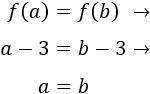
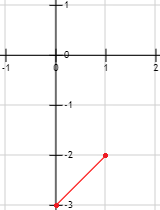
Gráfica:
Problema 3
Hallar \(b\) para que la función \(g(x) = x^2 -4x +5\) cumpla las hipótesis del teorema de Rolle en el intervalo \(\left[0,b\right]\) y calcular el número \(c\) del teorema.
Ver solución
La continuidad y la derivabilidad no son un problema puesto que la función es polinómica.
La otra condición es que \(g(0) = g(b)\). Como \(g(0)=5\), tenemos que buscar un \(b > 0\) tal que \(g(b) = 5\). Resolvemos la ecuación:
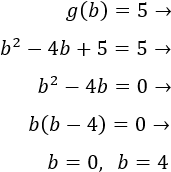
Por tanto, el \(b\) que buscamos es \(b = 4\) y el intervalo que tenemos es \(\left[0, 4\right]\).
Para obtener \(c\), calculamos la derivada, igualamos a 0 y resolvemos la ecuación:
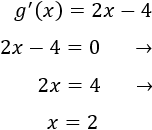
El punto \(c\) del teorema es \(c = 2\).
Gráfica:
Problema 4
Sea la función definida a trozos
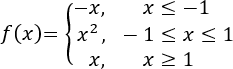
Determinar en cuáles de los siguientes intervalos se verifican las hipótesis del teorema de Rolle:
![intervalos [-2,-1], [-1,1], [0,1] y [-0.5,0.5] demostración del teorema de Rolle y problemas resueltos de aplicación](https://www.matesfacil.com/matematicos/Rolle/P4b.png)
Ver solución
Primero calculamos la imagen de la función en los extremos de los intervalos para ver si coinciden:
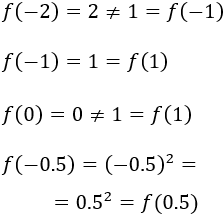
Por tanto, los intervalos candidatos son el segundo y el cuarto.
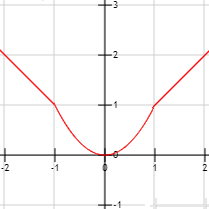
En el cuarto intervalo se verifican las condiciones porque la función \(x^2\) es continua en \(\left[-0.5, 0.5\right]\) y derivable en \(\left(-0.5, 0.5\right)\).
Veamos si se verifican en el segundo intervalo:
La función \(x^2\) es derivable en \(\left(-1, 1\right)\) por ser polinómica. También es continua en \(\left[-1, 1\right]\) porque los límites laterales en los extremos coinciden con la imagen de la función en los extremos.
Gráfica:
Problema 5
Estudiar si la siguiente función segmentada verifica las hipótesis del teorema de Rolle en el intervalo \(\left[-1, 1 \right]\):
![función segmentada h(x) = x^2 si x pertenece a [-1,0] y h(x) = x si x pertenece a ]0,1] demostración del teorema de Rolle y problemas resueltos de aplicación](https://www.matesfacil.com/matematicos/Rolle/P5.png)
Ver solución
Se cumple \(h(-1) = 1 = h(1)\).
La función es continua en el intervalo \(\left(-1, 1 \right)\) porque tanto \(x^2\) como \(x\) son continuas en su dominio y los límites laterales de \(h\) cuando \(x\) tiende a 0 coinciden con \(h(0) = 0\).
Estudiamos la derivabilidad:
El único punto problemático es donde cambia la definición de la función (\(x = 0\)). La derivada de \(h\) es
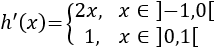
Obsérvese que hemos excluido el punto \(x = 0\) del dominio. La razón de ello es que las derivadas laterales en dicho punto no coinciden y, por tanto, \(h\) no es derivable en todo el intervalo \(\left(-1, 1 \right)\).
No se verifican las hipótesis del teorema de Rolle.
Gráfica:
![gráfica de la función segmentada h(x) = x^2 si x pertenece a [-1,0] y h(x) = x si x pertenece a ]0,1] demostración del teorema de Rolle y problemas resueltos de aplicación](https://www.matesfacil.com/matematicos/Rolle/P5g.png)
Problema 6
Hallar, si es posible, el parámetro \(a\) para que la siguiente función definida a trozos verifique las condiciones del teorema de Rolle en el intervalo \(\left[-1.5, 3\right]\) :
![función definida a trozos f(x) = ax +5 si x pertenece a [-1.5, 0] y f(x) = x^2 - 2x + 5 si x pertenece a ]0,3] demostración del teorema de Rolle y problemas resueltos de aplicación](https://www.matesfacil.com/matematicos/Rolle/P6.png)
Ver solución
Como la función debe valer lo mismo en los extremos del intervalo,
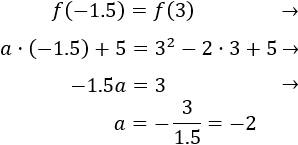
Hemos calculado el parámetro para que se verifique una de las condiciones, pero tenemos que comprobar si también se verifican las otras.
Para estudiar la continuidad calculamos los límites laterales en \(x = 0\):
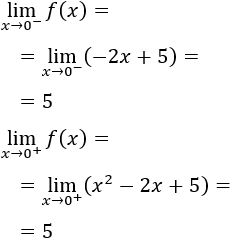
Se cumple la continuidad.
Calculamos la derivada:
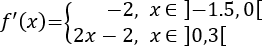
A la izquierda de \(x = 0\) la derivada es
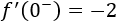
Y a la derecha es
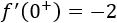
Como coinciden, la función es derivable en todo el intervalo \(\left(-1.5, 3\right)\).
Se verifican las hipótesis del teorema de Rolle para \(a = -2\).
Gráfica:
![gráfica de la función definida a trozos f(x) = ax +5 si x pertenece a [-1.5, 0] y f(x) = x^2 - 2x + 5 si x pertenece a ]0,3] demostración del teorema de Rolle y problemas resueltos de aplicación](https://www.matesfacil.com/matematicos/Rolle/P6g.png)
Problema 7
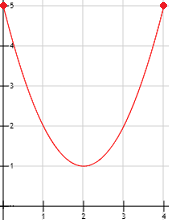
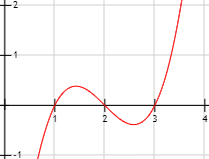
Observando la siguiente gráfica, proporcionar un intervalo cerrado donde la función representada verifique las hipótesis del teorema de Rolle. ¿Cuál es el punto \(c\) del teorema?
Ver solución
Hay varias posibilidades:
Para el intervalo \(\left[1, 2\right]\) se verifican las hipótesis y \(c \approx 1.5\).
Para el intervalo \(\left[2, 3\right]\) también se verifican y \(c \approx 2.5\).
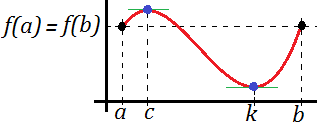
Además de estos dos, también se verifican para algunos intervalos que contienen a alguno de estos dos o a los dos. Por ejemplo, para el intervalo \(\left[1, 3\right]\) también se verifican las condiciones y en este caso hay dos puntos \(c\) donde se anula la derivada (los extremos relativos), que coinciden con los \(c\) de los intervalos anteriores.
Se pueden escoger un gran número de intervalos, pero solo hay dos posibilidades para \(c\).

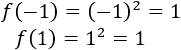
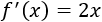
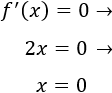

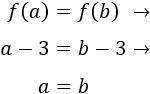

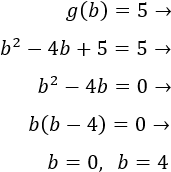
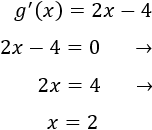

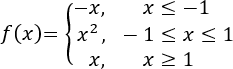
![intervalos [-2,-1], [-1,1], [0,1] y [-0.5,0.5] demostración del teorema de Rolle y problemas resueltos de aplicación](https://www.matesfacil.com/matematicos/Rolle/P4b.png)
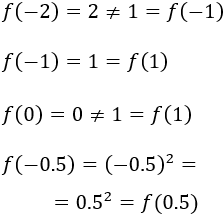

![función segmentada h(x) = x^2 si x pertenece a [-1,0] y h(x) = x si x pertenece a ]0,1] demostración del teorema de Rolle y problemas resueltos de aplicación](https://www.matesfacil.com/matematicos/Rolle/P5.png)
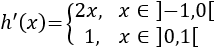
![gráfica de la función segmentada h(x) = x^2 si x pertenece a [-1,0] y h(x) = x si x pertenece a ]0,1] demostración del teorema de Rolle y problemas resueltos de aplicación](https://www.matesfacil.com/matematicos/Rolle/P5g.png)
![función definida a trozos f(x) = ax +5 si x pertenece a [-1.5, 0] y f(x) = x^2 - 2x + 5 si x pertenece a ]0,3] demostración del teorema de Rolle y problemas resueltos de aplicación](https://www.matesfacil.com/matematicos/Rolle/P6.png)
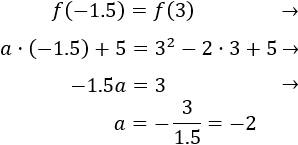
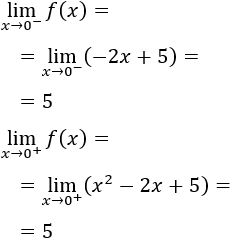
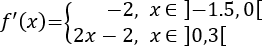
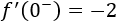
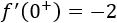
![gráfica de la función definida a trozos f(x) = ax +5 si x pertenece a [-1.5, 0] y f(x) = x^2 - 2x + 5 si x pertenece a ]0,3] demostración del teorema de Rolle y problemas resueltos de aplicación](https://www.matesfacil.com/matematicos/Rolle/P6g.png)



