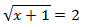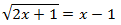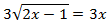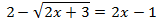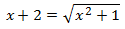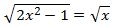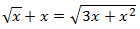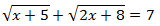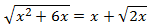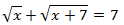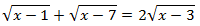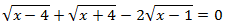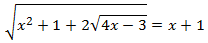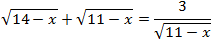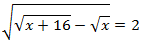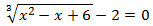Contenido de esta página:
Una ecuación irracional es una ecuación
en la que aparecen raíces que contienen a la incógnita en su radicando,
es decir, la incógnita se encuentra bajo signos radicales.
Para resolverlas, se elevan ambos lados de la ecuación al orden de la raíz (al cuadrado, al cubo...).
Esto nos obligará a calcular binomios de Newton como el cuadrado de la suma:
$$ ( a + b )^2 = a^2 + b^2 + 2a\cdot b $$
por lo que tendremos que escribir la ecuación de modo que no se compliquen los cálculos (por ejemplo, aislar la raíz en uno de los dos lados de la igualdad).
Este procedimiento aumenta el grado de la ecuación, por lo que posiblemente estamos añadiendo soluciones. Es por ello por lo que siempre
comprobaremos las soluciones.
Otro problema que conlleva esta potenciación, en el caso de las raíces de orden par, es que debemos asegurarnos de que las expresiones de los radicandos son positivas o cero (una vez encontrada la solución) para que exista la raíz.
En esta sección resolvemos ecuaciones irracionales. Los ejercicios pretenden estar ordenados en orden creciente de dificultad: empezaremos con ecuaciones simples con una sola raíz cuadrada. Luego tendremos dos o tres raíces en la misma ecuación e incluso raíces en los denominadores.
También veremos un ejercicio con una raíz cúbica y otros con raíces anidadas (una raíz dentro de otra).
Respecto a los radicandos, serán, sobre todo, expresiones polinómicas de primer grado.
Temas similares: ecuaciones logarítmicas y sistemas y ecuaciones exponenciales.
Vamos a explicar el método de resolución a través de un ejemplo:
$$ \sqrt{x-1} -1 =0 $$
Reordenamos la ecuación: aislamos la raíz en uno de los lados:
$$ \sqrt{x-1} = 1 $$
-
Elevamos ambos lados al orden de la raíz. Si la raíz es cuadrada, elevamos a 2; si
es cúbica, elevamos a 3; si es de orden 4, elevamos a 4...
$$ (\sqrt{x-1})^2 = 1^2 $$
-
Desarrollamos las potencias. En nuestro ejemplo, el signo radical desaparece y el
cuadrado de 1 es 1:
$$ x-1 = 1 $$
Si quedan raíces, vamos de nuevo al primer paso. Si no quedan raíces, resolvemos la
ecuación:
$$ x-1 = 1 $$
$$ x = 1+1 $$
$$ x = 2 $$
-
Comprobamos que las soluciones son realmente soluciones:
Sustituimos x = 2 en la ecuación inicial:
$$ \sqrt{x-1} -1 = 0 $$
$$ \sqrt{2-1} -1 = 0 $$
$$ \sqrt{1} -1 = 0 $$
$$ 1-1 = 0 $$
$$ 0 = 0 $$
Por tanto, x = 2 es una solución.
Ecuación 1
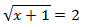
Solución
Como tenemos una raíz cuadrada, elevamos al cuadrado ambos lados de la ecuación:
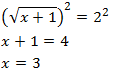
Comprobamos la solución:
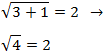
Por tanto, es solución.
Nota: si pasamos el 2 a la izquierda de la igualdad antes de hacer el cuadrado, tendríamos
que calcular el cuadrado de una resta, por lo que seguiría quedando una raíz:
$$\sqrt{x+1} -2 = 0$$
Tenemos que aplicar la regla del binomio de Newton:
$$( a + b )^2 = a^2 + b^2 + 2ab$$
Por tanto,
$$\left( \sqrt{x+1} -2 \right) ^2 = 0^2$$
$$(x+1) + 4 -4 \sqrt{x+1} = 0$$
Podemos observar que estamos complicando más la ecuación inicial.
Tenemos que dejar siempre una raíz aislada a un lado de la igualdad.
Ecuación 2
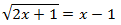
Solución
Como tenemos una raíz cuadrada, elevamos al cuadrado ambos lados de la ecuación. No olvidemos la fórmula del cuadrado de la resta (lado derecho):
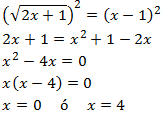
Comprobamos las soluciones:
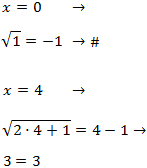
Por tanto, la única solución es x = 4.
Ecuación 3
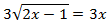
Solución
Elevamos al cuadrado ambos lados de la ecuación obteniendo una
ecuación de segundo grado:
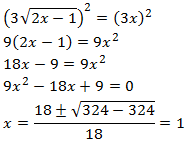
La única solución de la ecuación de segundo grado es
x = 1. Comprobamos si es la solución de la ecuación irracional:
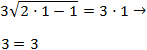
Por tanto, es solución.
Ecuación 4
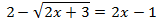
Solución
Elevamos al cuadrado ambos lados de la ecuación, pero para que realmente desaparezca la raíz tenemos que aislarla en un lado de la ecuación:

Comprobamos las soluciones obtenidas:
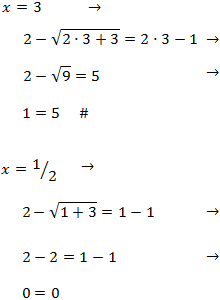
Por tanto, la única solución es x = 1/2.
Nota: en el primer paso hemos aislado la raíz
cuadrada en un lado de la igualdad. Si no, no habría desaparecido:
$$ (2-\sqrt{2x+3})^2 = (2x-1)^2 $$
$$ 4 + (2x+3) -2\cdot 2 \cdot \sqrt{2x+3}= (2x-1)^2 $$
Ecuación 5
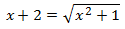
Solución
Elevamos al cuadrado ambos lados de la ecuación y resolvemos la ecuación obtenida:
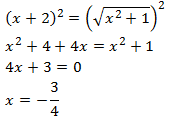
Comprobamos la solución:
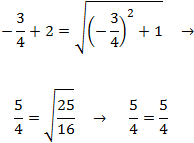
Por tanto, es solución.
Ecuación 6
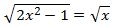
Solución
Como tenemos una raíz cuadrada en cada lado, elevamos al cuadrado ambos lados de la igualdad y ambas raíces desaparecerán:
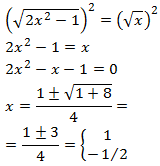
Comprobamos las soluciones obtenidas:
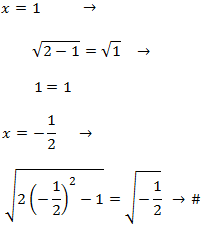
Por tanto, la única solución es x = 1.
Nota: realmente, x = -1/2 sí es solución porque
al sustituir se obtiene la igualdad entre complejos
$$ \frac{\sqrt{2}}{2}i = \frac{\sqrt{2}}{2}i $$
Pero no contemplamos esta situación en este nivel.
Ecuación 7
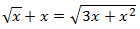
Solución
Elevamos al cuadrado ambos lados de la igualdad:
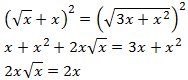
Elevamos al cuadrado otra vez para que desaparezca la raíz que queda:
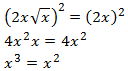
Resolvemos la ecuación de tercer grado por factorización:
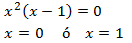
Finalmente, comprobamos ambas soluciones:
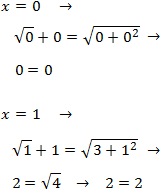
Por tanto, ambas son soluciones.
Ecuación 8
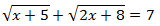
Solución
Como tenemos raíces cuadradas, elevamos al cuadrado ambos lados de la ecuación. Tenemos que aplicar la fórmula del cuadrado de la suma:
$$( a + b )^2 = a^2 + b^2 + 2ab$$
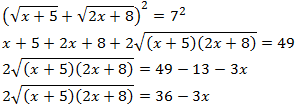
Seguimos teniendo una raíz cuadrada, así que elevamos al cuadrado otra vez:
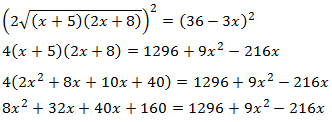
Resolvemos la ecuación de segundo grado:
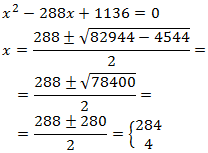
Finalmente, comprobamos las soluciones:
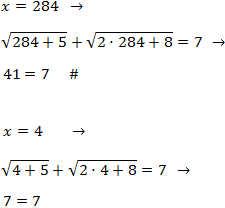
Por tanto, la única solución es x = 4.
Ecuación 9
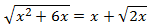
Solución
Elevamos al cuadrado para eliminar las raíces (tendremos que hacerlo dos veces) y resolvemos
la ecuación de segundo grado (factorizando):
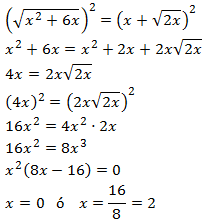
Comprobamos las soluciones:
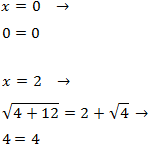
Por tanto, ambas son soluciones.
Ecuación 10
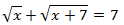
Solución
Tenemos que elevar al cuadrado dos veces y aplicar la regla del Binomio de Newton (cuadrado de la suma):

Comprobamos la solución:
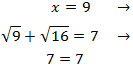
Por tanto, es solución.
Ecuación 11
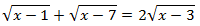
Solución
Elevamos al cuadrado ambos lados de la ecuación dos veces para eliminar las tres raíces (tendremos que aplicar el bonomio de Newton):
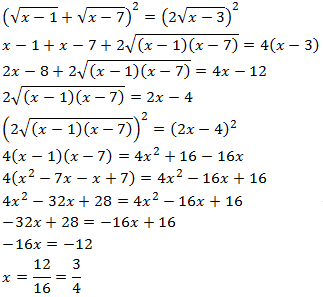
Comprobamos la solución:
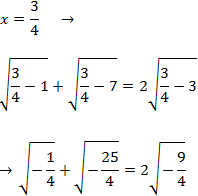
Por tanto, no hay soluciones reales (porque no existen las raíces de números negativos).
Ecuación 12
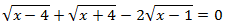
Solución
Antes de elevar al cuadrado (dos veces), pasamos una raíz al otro lado. Si no, tendremos que calcular el cuadrado del cubo, cuyo desarrollo es más largo que el de la suma:
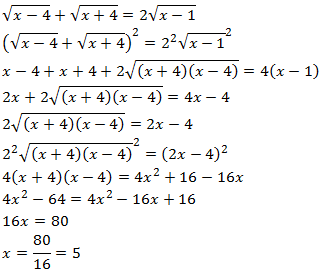
Comprobamos la solución:
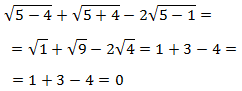
Como se cumple la ecuación, es la solución.
Ecuación 13
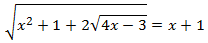
Solución
Elevamos al cuadrado ambos lados de la ecuación (dos veces) sin preocuparnos de que haya una raíz en el radicando de otra:
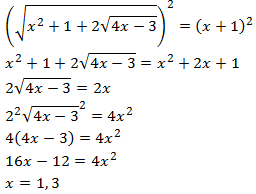
Comprobamos las soluciones:
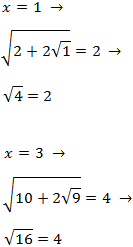
Por tanto, ambas son solución.
Ecuación 14
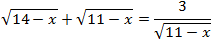
Solución
Lo primero que haremos es multiplicar toda la ecuación
por la raíz del denominador para evitar las fracciones.
No olvidemos que x no puede ser 11 para que no haya
un 0 en el denominador. Después, elevamos al cuadrado ambos
lados de la ecuación:
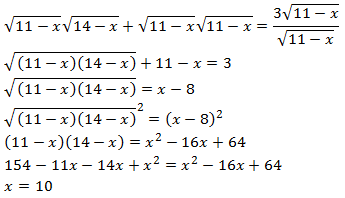
Comprobamos la solución:
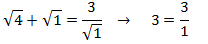
Por tanto, es solución.
Ecuación 15
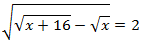
Solución
Elevamos al cuadrado dos veces y resolvemos la
ecuación de segundo grado:
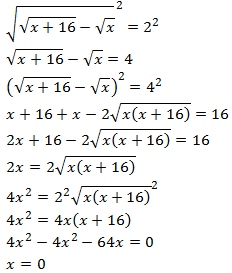
Comprobamos la solución:
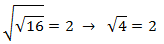
Por tanto, es solución.
Ecuación 16
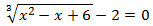
Solución
Como tenemos una raíz cúbica, elevamos al cubo ambos lados de la ecuación.
Para evitar tener que usar la fórmula del trinomio al cubo, escribimos el -2 al otro lado de la ecuación:
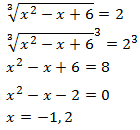
Comprobamos las soluciones:
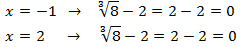
Por tanto, ambas son solución.
Ecuación 17
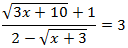
Solución
Antes de elevar al cuadrado (dos veces), multiplicamos la ecuación por el denominador para evitar las fracciones (pasamos el denominador multiplicando en el lado derecho).
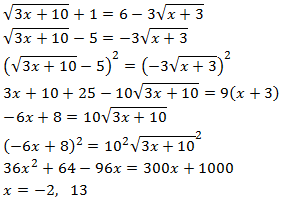
Comprobamos las soluciones:
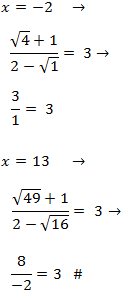
Por tanto, la única solución es x = - 2.