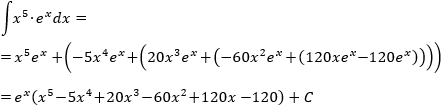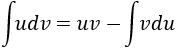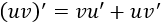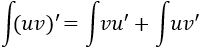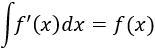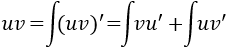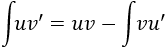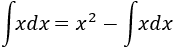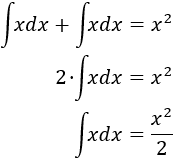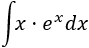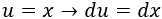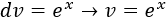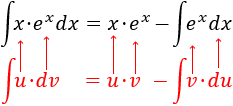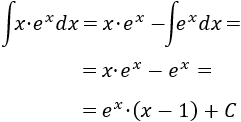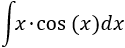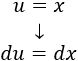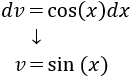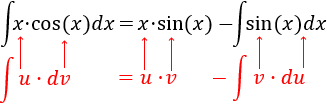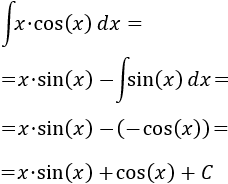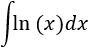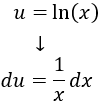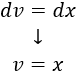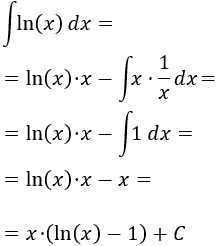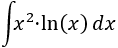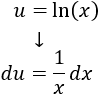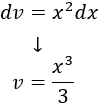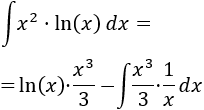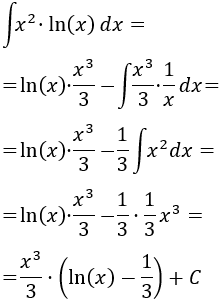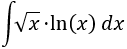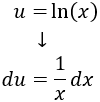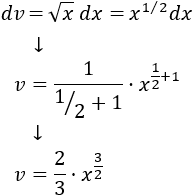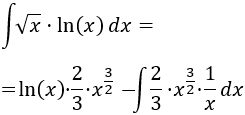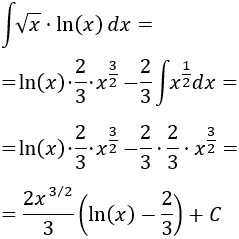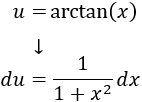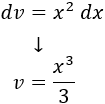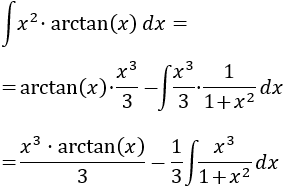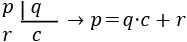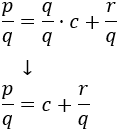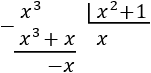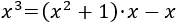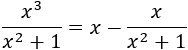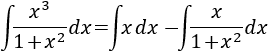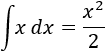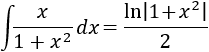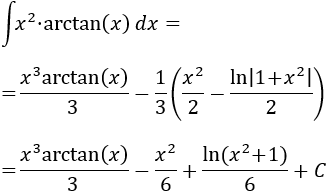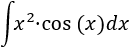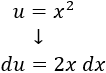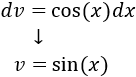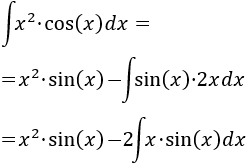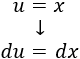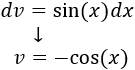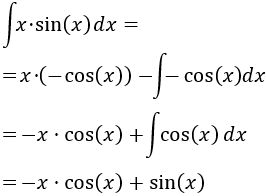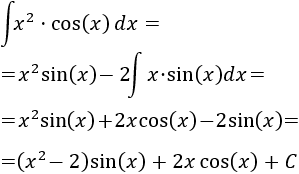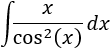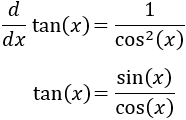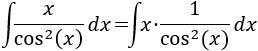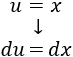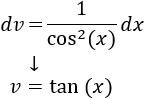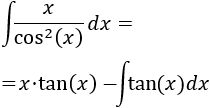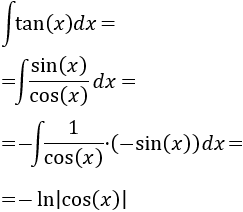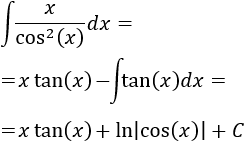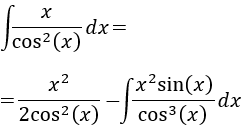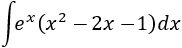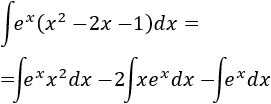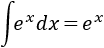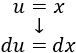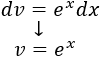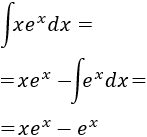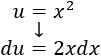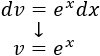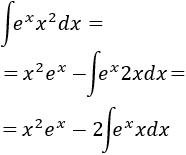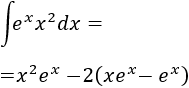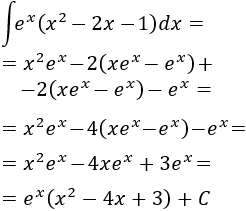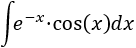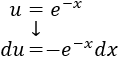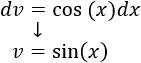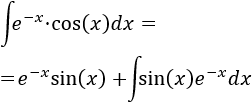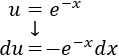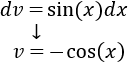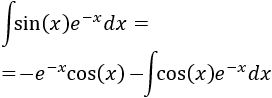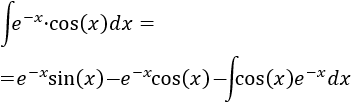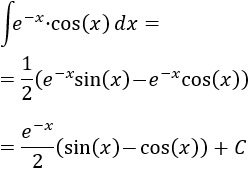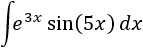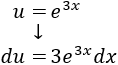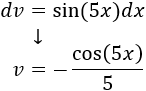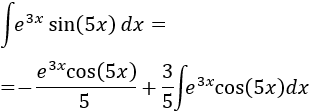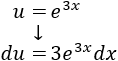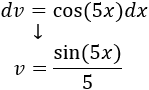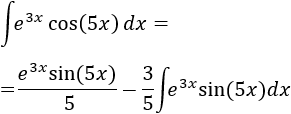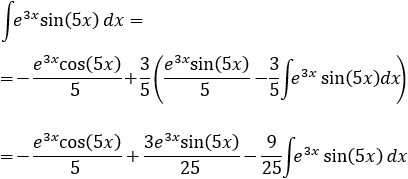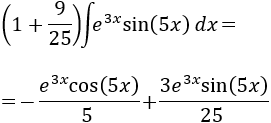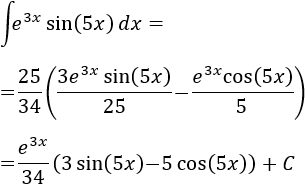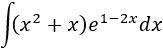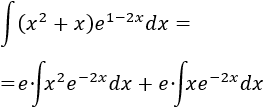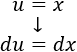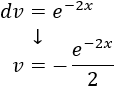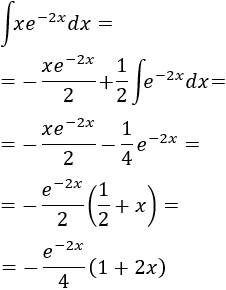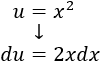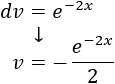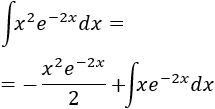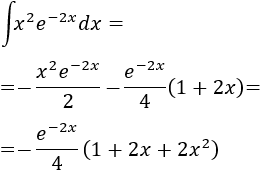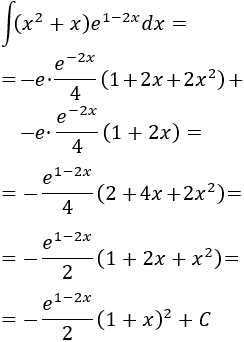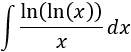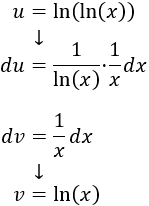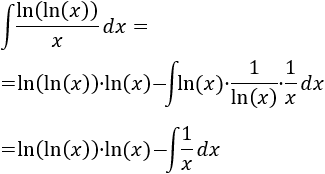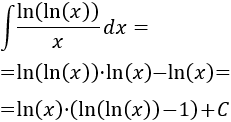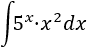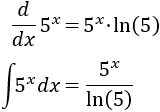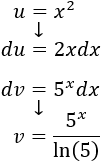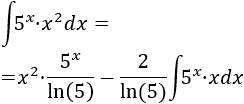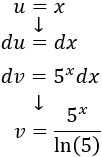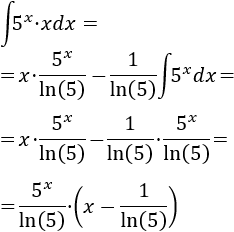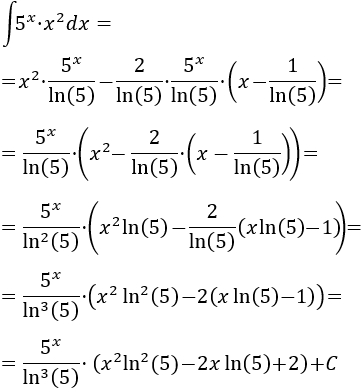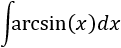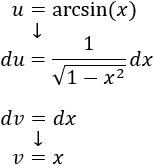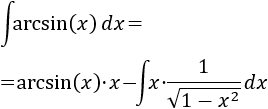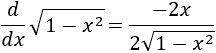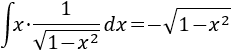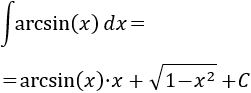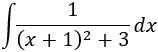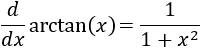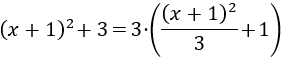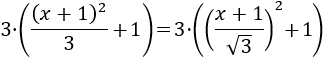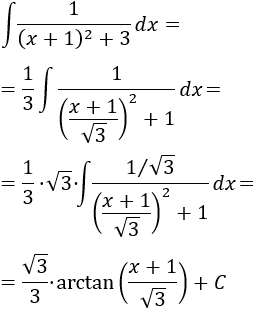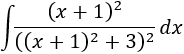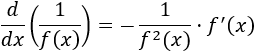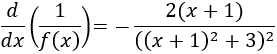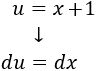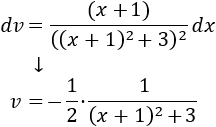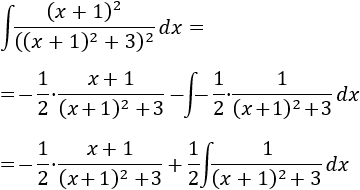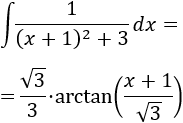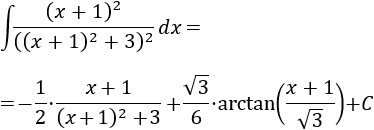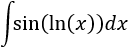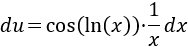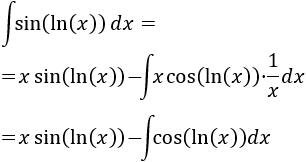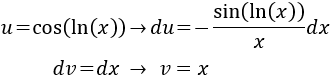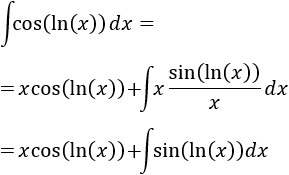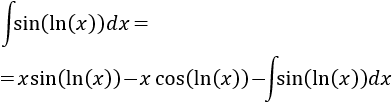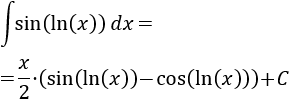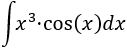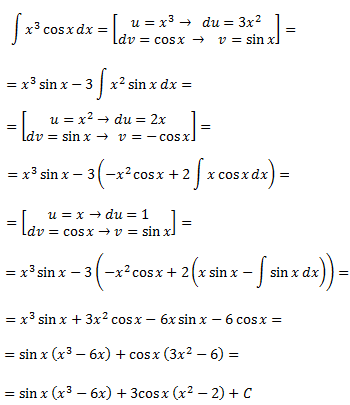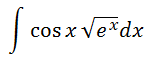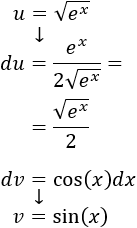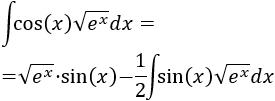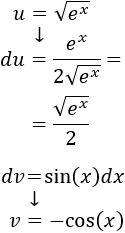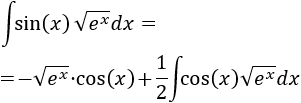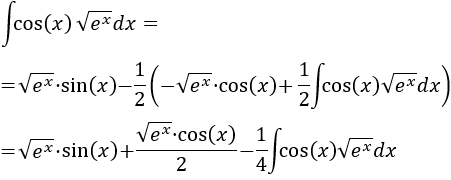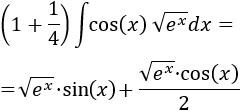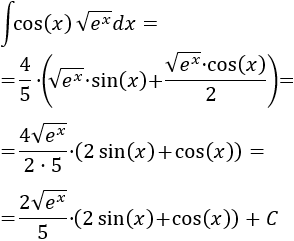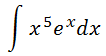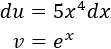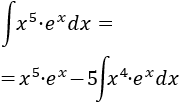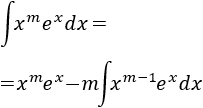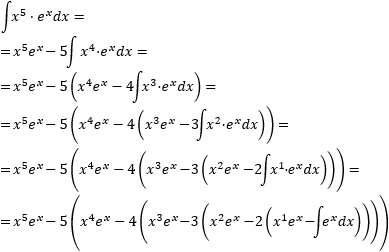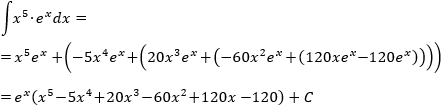Integral 1 
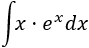
SOLUCIÓN
Tenemos el producto \(x\cdot e^x\).
Observad que la exponencial no cambia al derivar ni al integrar, así que no importa si le asignamos \(u\) ó \(dv\).
No ocurre lo mismo con \(x\):
-
Al derivar se reduce su exponente en 1 y pasa a ser una constante.
-
Al integrar aumenta su exponente en 1.
Por tanto, la elección más apropiada es \(u = x\) y \(du = dx\).
Derivamos \(u\) para calcular \(du\):
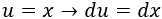
Integramos \(dv\) para calcular \(v\):
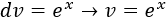
Aplicamos la fórmula de integración por partes:
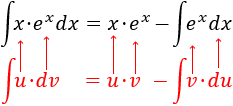
Finalmente, resolvemos la nueva integral (la de la exponencial) y añadimos la constante de integración \(C\in \mathbb{R}\):
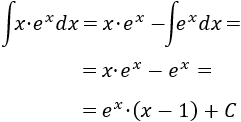
Nota: como ya hemos dicho, es importante escoger \(x = u\) para reducir el grado del monomio al derivar. Si por el
contrario hubiésemos escogido \(x = dv\), entonces \(v = \frac{x^2}{2}\), aumentando el grado (de 1 a 2) y complicando más la integral, pues el factor de la exponencial
se mantiene igual y nos aparece la integral
$$ \int {\frac{x^2}{2}\cdot e^x }dx$$
Comentario:
-
En la integral anterior hemos considerado \(dv = dx\), pero algunos autores habrían escrito simplemente \(dv = 1\) (es decir, sin \(dx\)). No es algo que afecte a la resolución de la integral.
-
También, podemos encontrar puntos multiplicativos en la fórmula de integración por partes, como en \(\int{v\cdot du}\), que facilitan diferenciar los elementos de la fórmula.
Integral 2 
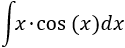
SOLUCIÓN
Tenemos el producto \(x\cdot \cos(x)\).
Observad que no importa si \(\cos(x)\) es \(u\) ó \(dv\), ya que obtenemos un seno tanto si derivamos como si integramos. Sin embargo, ya sabemos que es mejor considerar \(u = x\) para reducir su grado.
Derivamos \(u = x\) para calcular \(du\):
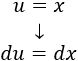
Integramos \(dv = \cos(x)dx\) para calcular \(v\):
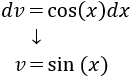
Aplicamos la fórmula de integración por partes:
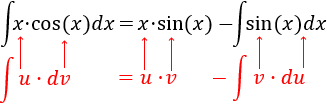
Solo queda calcular la integral de \(\sin(x)\), que es \(-\cos(x)\), y añadir la constante de integración \(C\in\mathbb{R}\):
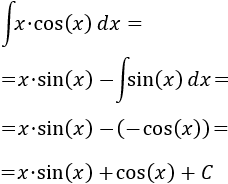
Nota: si hubiésemos tomado la elección \(u = \cos(x)\) y \(dv = xdx\), entonces tendríamos \(du = -\sin(x)dx\) y \(v = x^2/2\). De este modo, habríamos complicado la integral ya que habría aparecido la integral
$$ \int{\frac{x^2\sin(x)}{2}}dx $$
Integral 3 
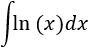
SOLUCIÓN
Podemos ver el integrando como un producto: \(1\cdot \ln(x)\).
En esta integral sólo hay una posibilidad de elección y debe ser \(u=\ln(x)\) y \(dv = dx\) (ya que si escogemos \(dv = \ln(x)dx\), deberíamos calcular la integral que queremos resolver para tener \(v\)).
Derivamos \(u\) para calcular \(du\):
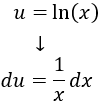
Integramos \(dv\) para calcular \(v\):
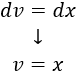
Aplicamos la fórmula de integración por partes:
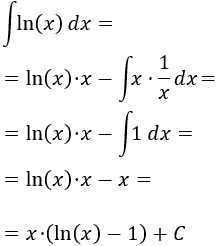
Integral 4 
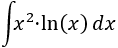
SOLUCIÓN
En un principio, nos interesa considerar \(u = x^2\) para reducir su exponente al derivar. Pero entonces, deberíamos integrar \(dv = \ln(x)dx\), lo cual no es una buena idea (aunque previamente hemos calculado dicha integral). Por tanto, escogemos \(u = \ln(x)\) y \(dv = x^2 dx\).
Derivamos \(u\) para calcular \(du\):
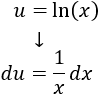
Integramos \(dv\) para calcular \(v\):
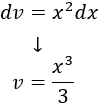
Aplicamos la fórmula de integración por partes:
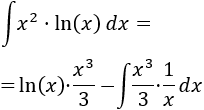
En el integrando tenemos una constante (1/3) que podemos extraer y un cociente de potencias de \(x\) que podemos simplificar:
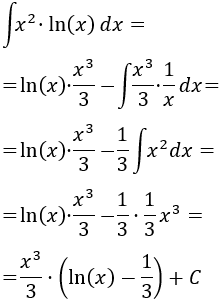
Integral 5 
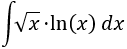
SOLUCIÓN
La única dificultad de esta integral es integrar la raíz cuadrada.
Como ya hemos venido diciendo, escogemos \(u = \ln(x)\) y, por tanto, \(dv = \sqrt{x}dx\).
Derivamos \(u\) para calcular \(du\):
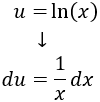
Integramos \(dv\) para calcular \(v\) (escribiendo la raíz cuadrada como una potencia):
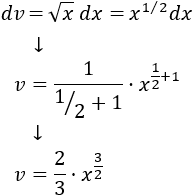
Aplicamos la fórmula de integración por partes:
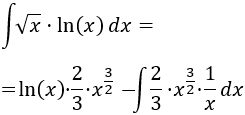
Operamos un poco y resolvemos:
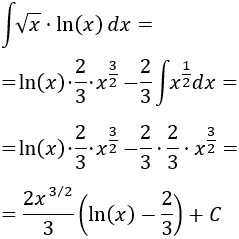
Integral 6 

SOLUCIÓN
La dificultad de esta integral se debe a que debemos saber resolver integrales de funciones racionales (cociente de polinomios), además de que debemos saber la derivada de la arcotangente.
Como no es fácil de integrar la arcotangente, escogemos \(u = \arctan(x)\) y \(dv = x^2\).
Derivamos \(u\) para calcular \(du\):
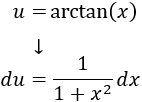
Integramos \(dv\) para calcular \(v\):
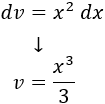
Aplicamos la fórmula de integración por partes:
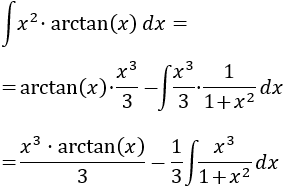
Ahora debemos integrar el cociente de polinomios \(x^3/(1+x^2)\).
-
Como el grado del polinomio del denominador es menor que el del numerador, no se trata de la derivada de un logaritmo.
- Por tanto, la siguiente opción es efectuar la división de polinomios para reescribir el cociente como una suma de fracciones.
Recordad que cuando dividimos \(p/q\) obtenemos un cociente \(c\) y un resto \(r\), de modo que \(p =q\cdot c + r\):
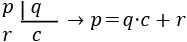
Dividimos la igualdad anterior entre \(q\):
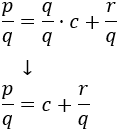
Nosotros vamos a considerar \(p = x^3\) (numerador) y \(q = 1+x^2\) (denominador). Así, aplicando la identidad anterior, podremos escribir el cociente del integrando como la suma \(c + r/q\) y, de este modo, descomponer la integral en una suma de integrales más sencillas.
Necesitamos para ello calcular el cociente \(r\) y \(q\), y lo haremos efectuando la división de polinomios:
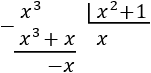
La división ha terminado, así que tenemos
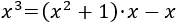
Con lo que
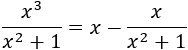
Luego tenemos
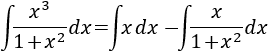
La primera de las integrales es directa:
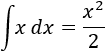
La segunda tiene por integrando casi la derivada de un logaritmo:
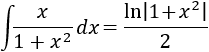
Por tanto, el resultado de la integral inicial es
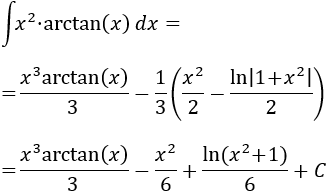
Nota: en el logaritmo no es necesario el valor absoluto ya que \(1+x^2\) es siempre positivo.
Integral 7 
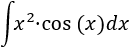
SOLUCIÓN
La dificultad de esta integral solo consiste en que debemos aplicar integración por partes dos veces.
Integrar o derivar \(\cos(x)\) nos proporciona \(\pm \sin(x)\), así que no mejora la situación. Luego escogemos \(u = x^2\) para rebajar su grado al derivar y \(dv = cos(x) dx\).
Derivamos \(u\) para calcular \(du\):
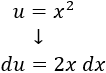
Integramos \(dv\) para calcular \(v\):
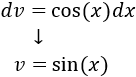
Aplicamos la fórmula de integración por partes:
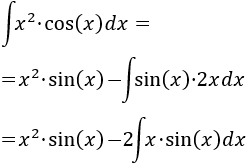
Como ya hemos indicado, debemos aplicar de nuevo integración por partes para calcular la integral obtenida. Debemos mantener la elección anterior: \(u = x\) y \(dv = \sin(x)\). En caso contrario, deshacemos el paso anterior.
Derivamos \(u\) para calcular \(du\):
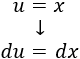
Integramos \(dv\) para calcular \(v\):
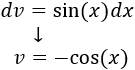
Aplicamos la fórmula de integración por partes:
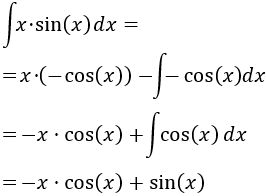
Por tanto, la integral inicial es
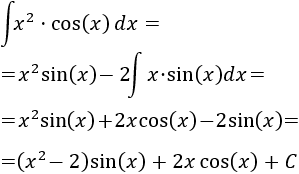
Integral 8 
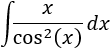
SOLUCIÓN
La dificultad de esta integral consiste en que debemos conocer la derivada de la tangente y que podemos escribir la tangente como el cociente de seno y coseno:
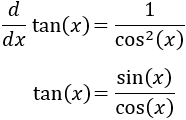
Nota: la notación \(\frac{d}{dx}f(x)\) equivale a \(f’(x)\).
En primer lugar, debemos observar que tenemos un cociente en lugar de un producto en el integrando, pero esto es fácil de solucionar:
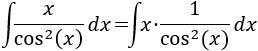
La elección de \(u\) y \(dv\) también es clara:
-
De un lado, siempre conviene tomar \(u = x\):
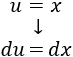
-
De otro, es más rápido integrar \(1/\cos^2(x)\) que derivarlo:
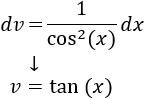
Aplicamos la fórmula de integración por partes:
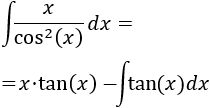
Escribimos la tangente como un cociente para facilitar la integración:
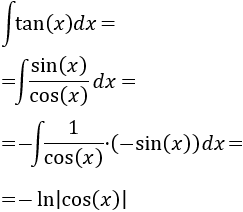
Luego la integral inicial es
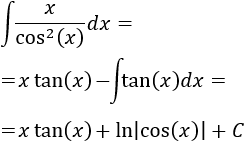
Nota: si hubiésemos escogido \(u = 1/\cos^2(x)\) y \(dv = xdx\), entonces habríamos tenido
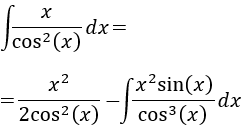
Huelga decir que la integral que se obtiene es más difícil que la inicial.
Integral 9 
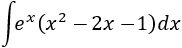
SOLUCIÓN
Si desarrollamos el producto del integrando, éste pasa a ser una suma, lo cual nos permite descomponer la integral en 3 integrales más sencillas:
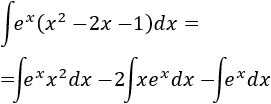
La tercera de las integrales es directa:
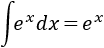
Ahora vamos a calcular la segunda integral por partes, considerando \(u = x\) y \(dv = e^xdx\).
Derivamos \(u\) para calcular \(du\):
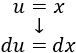
Integramos \(dv\) para calcular \(v\):
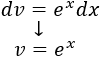
Aplicamos la fórmula de integración por partes:
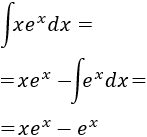
Ahora, calculamos la primera integral considerando \(u = x^2\) y \(dv = e^xdx\).
Derivamos \(u\) para calcular \(du\):
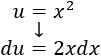
Integramos \(dv\) para calcular \(v\):
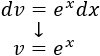
Aplicamos la fórmula:
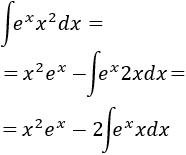
Observad que ya hemos calculado anteriormente la integral de \(xe^x\), así que
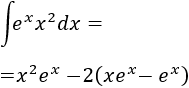
Luego la integral inicial es
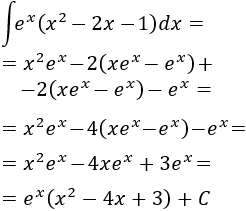
Integral 10 

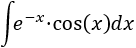
SOLUCIÓN
El procedimiento, y no la integral en sí, es importante, ya que, una vez aplicada la integración por partes (dos veces), tenemos que despejar la integral como lo haríamos en una ecuación. Es una integral cíclica.
En esta integral nos es indiferente escoger una u otra función del producto del integrando para \(u\) y \(dv\). Sea, pues, por ejemplo, \(u = e^{-x}\) y \(dv = \cos(x)\).
Derivamos \(u\) para calcular \(du\):
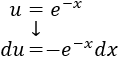
Integramos \(dv\) para calcular \(v\):
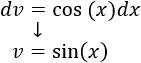
Aplicamos la fórmula de integración por partes:
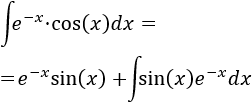
Aplicamos de nuevo integración por partes, siendo \(u = e^{-x}\) y \(dv = \sin(x)\) (ahora sí es importante esta elección, para no deshacer lo hecho).
Derivamos \(u\) para calcular \(du\):
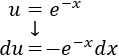
Integramos \(dv\) para calcular \(v\):
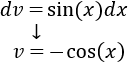
Aplicamos la fórmula:
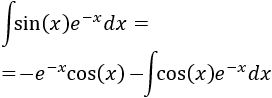
Por tanto, tenemos
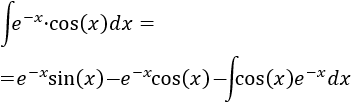
Luego, despejando la integral en la igualdad obtenemos
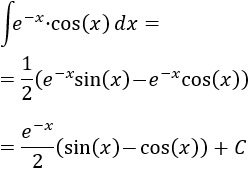
Nota: hemos despejado como lo haríamos en la ecuación \(x = a - x\), obteniendo \( x = a/2\).
Integral 11 
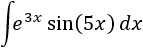
SOLUCIÓN
Clasificamos esta integral como difícil porque debemos integrar por partes dos veces y, además, tenemos que trabajar con signos y fracciones que complican las operaciones. Y, además, se trata de una integral cíclica.
Respecto a la elección de \(u\) y \(dv\), no tiene demasiada importancia ya que derivar o integrar la exponencial y el seno viene a ser lo mismo.
Sean, por ejemplo, \(u = e^{3x}\) y \(dv = \sin(5x)dx\).
Derivamos \(u\) para calcular \(du\):
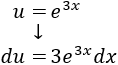
Integramos \(dv\) para calcular \(v\):
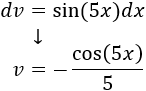
Aplicamos la fórmula de integración por partes:
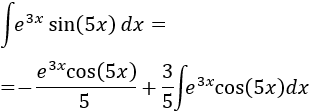
Aplicamos de nuevo integración por partes, con \(u = e^{3x}\) y \(dv = \cos(5x)\).
Derivamos \(u\):
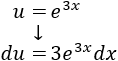
Integramos \(dv\):
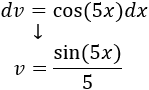
Luego, aplicando la fórmula,
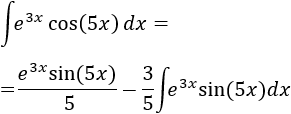
Tenemos, entonces
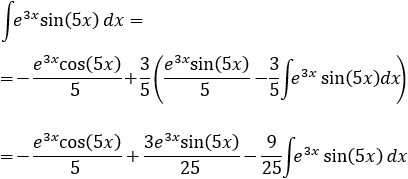
Despejamos la integral:
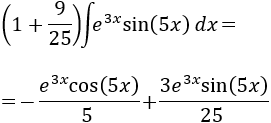
Nota: hemos aislado la integral como lo haríamos en la ecuación \(x = a-9x/25\), obteniendo \((1+9/25)x = a\).
Entonces,
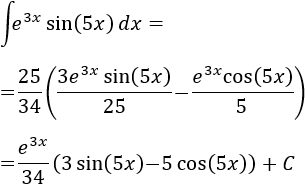
Nota: en el último paso hemos introducido el 25 en el paréntesis para evitar las fracciones.
Integral 12 
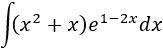
SOLUCIÓN
La dificultad de esta integral se debe a que tenemos que integrar por partes dos veces y a que la resolución es extensa, con lo que es probable cometer errores de cálculo.
Podemos descomponer la integral en una suma de integrales:
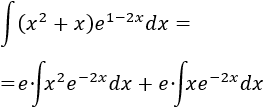
Empezamos por la segunda integral, asignando \(u = x\) y \(dv = e^{-2x}\).
Calculamos \(du\):
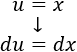
Integramos \(dv\):
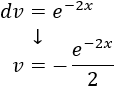
Aplicamos la fórmula:
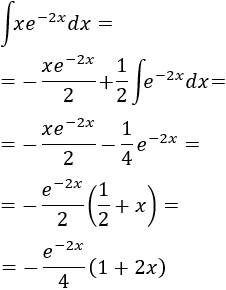
Ahora calculamos la primera integral, tomando \(u = x^2\) y \(dv = e^{-2x}dx\).
Derivamos \(u\):
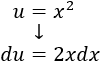
Integramos \(dv\):
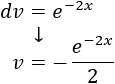
Aplicamos la fórmula:
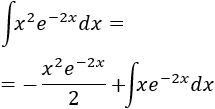
La integral de \(xe^{-2x}\) la hemos calculado, así que
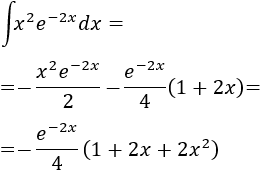
Por tanto, la integral inicial es (sumamos las dos integrales calculadas multiplicadas por \(e\)):
Integral 13 
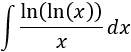
SOLUCIÓN
Como integrar el logaritmo es difícil, optaremos por considerar \(u = \ln(\ln(x))\) y \(dv = 1/x dx\):
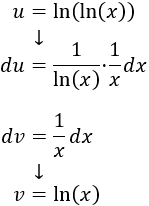
Aplicamos la fórmula:
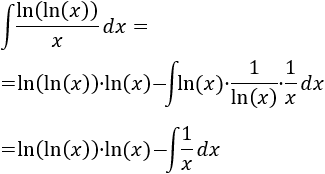
La integral que queda es directa (es un logaritmo). Por tanto,
Integral 14 
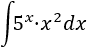
SOLUCIÓN
La mayor dificultad de esta integral es conocer la derivada/integral de una exponencial:
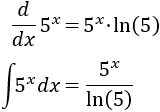
Integrar o derivar no afecta demasiado a la exponencial, así que nos conviene tomar \(u = x^2\) para rebajar el grado:
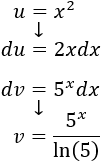
Aplicamos la fórmula:
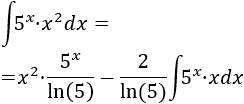
Aplicamos de nuevo integración por partes:
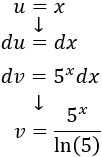
Luego
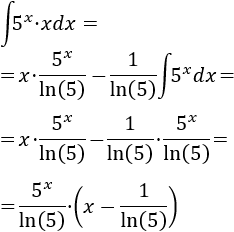
Por tanto, la integral inicial es
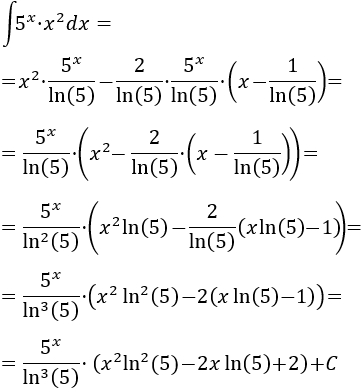
Integral 15 
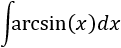
SOLUCIÓN
Esta integral es fácil siempre que sepamos derivar el arcoseno. Como integrar el arcoseno no es una opción, tomamos
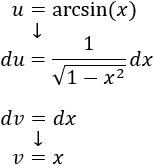
Aplicamos la fórmula de integración por partes:
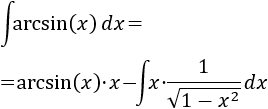
La integral que queda es directa, pues es casi la derivada de la raíz del integrando (le falta el signo negativo):
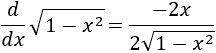
Por tanto,
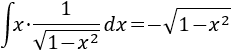
Luego
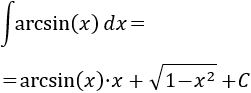
Integral 15B
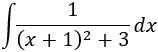
SOLUCIÓN
Integral directa (no requiere integración por partes).
Hemos añadido esta integral por la importancia de su procedimiento y porque hace falta en la siguiente integral.
Observemos que el denominador del integrando es un polinomio de grado 2, por lo que de ninguna manera el integrando puede ser la derivada de un logaritmo (haría falta un polinomio de grado 1 en el numerador).
Sin embargo, el integrando se asemeja en gran medida a la derivada de la arcotangente:
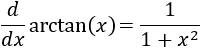
Lo que haremos es operar en el denominador del integrando para conseguir la derivada de una arcotangente.
Extraemos 3 como factor común:
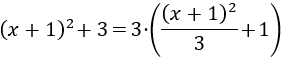
Introducimos el 3 en el cuadrado en forma de raíz cuadrada:
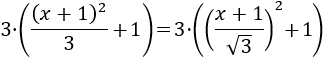
Ahora ya podemos integrar:
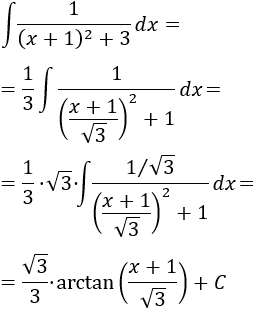
Integral 16 
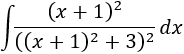
SOLUCIÓN
Vamos a hacer una explicación previa para entender mejor el procedimiento que vamos a seguir.
Recordad que la derivada de \(1/x\) es \(-1/x^2\). De esto podemos deducir la derivada del inverso de una función \(f(x)\):
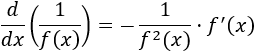
Ahora supongamos que \(f(x) = (x+1)^2+3\). Entonces, su derivada es
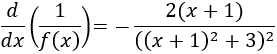
Esta derivada es casi nuestro integrando (sobra el -2 y falta un cuadrado), lo que nos permite considerar \(dv = -1/2·(1/f(x))'dx\) (y, por tanto,\(v = -1/2·1/f(x)\)) y \(u = x+1\).
Calculamos \(du\):
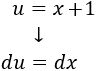
Calculamos \(v\):
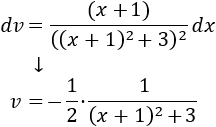
Aplicamos la fórmula:
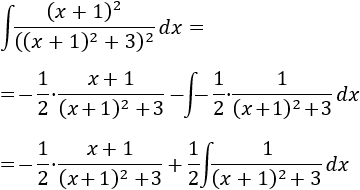
La integral que queda ya la hemos calculado anteriormente:
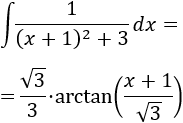
Por tanto,
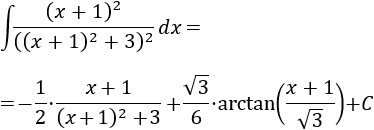
Integral 17 
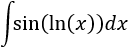
SOLUCIÓN
Desde luego debemos considerar al integrando como \(u\), así que
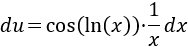
Y \(dv = dx\), con lo que \(v = x\).
Aplicamos la fórmula:
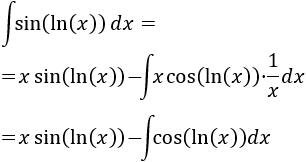
Podemos aplicar de nuevo por partes y obtendremos la integral inicial:
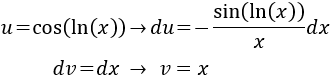
Aplicamos la fórmula:
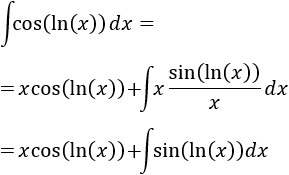
Por tanto, tenemos
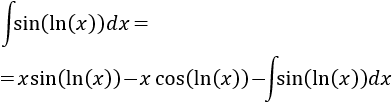
De donde deducimos
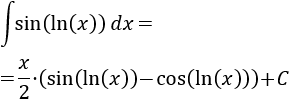
Integral 18 
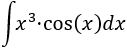
SOLUCIÓN
La dificultad consiste en que tenemos que aplicar 3 veces integración por partes:
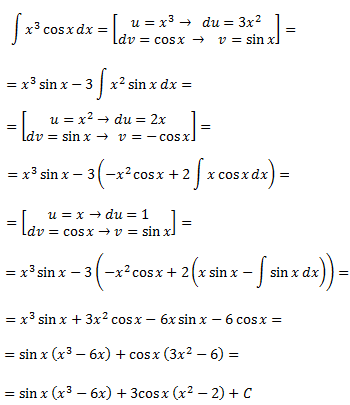
Integral 19 
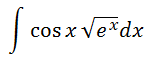
SOLUCIÓN
Será más fácil escoger la raíz como \(u\) y el coseno como \(dv\).
Calculamos \(du\) y \(v\):
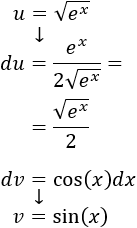
Aplicamos la fórmula:
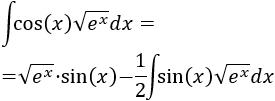
Aplicamos de nuevo integración por partes:
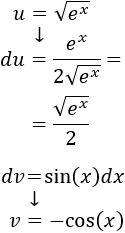
Por tanto,
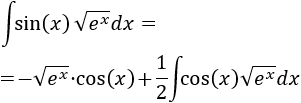
Luego tenemos
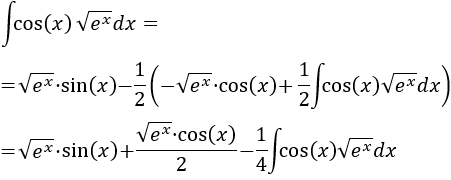
De donde
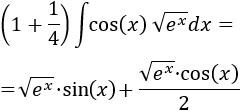
Despejando,
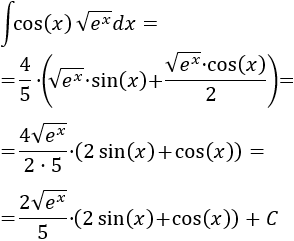
Integral 20 
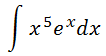
SOLUCIÓN
Lógicamente, escogemos \(u = x^5\) y \(dv = e^x\), así que
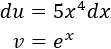
Aplicamos la fórmula:
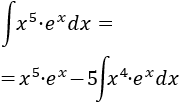
Ahora, deberíamos integrar por partes otras 4 veces, pero lo que hacemos es deducir, observando lo anterior, que
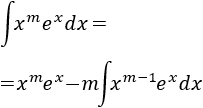
Por tanto, aplicando esta fórmula,
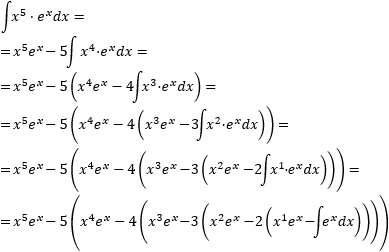
Simplificamos: