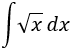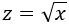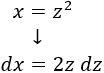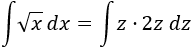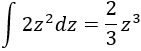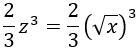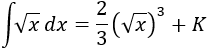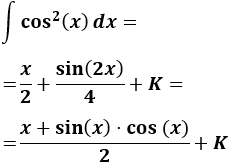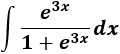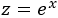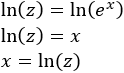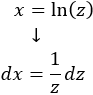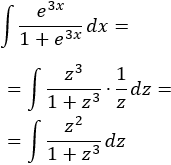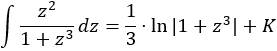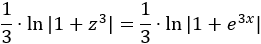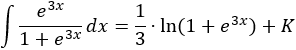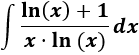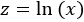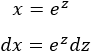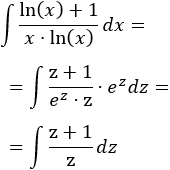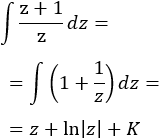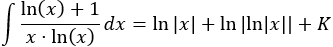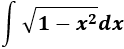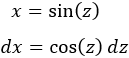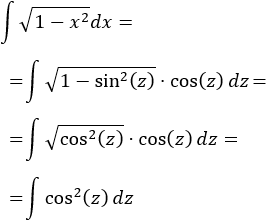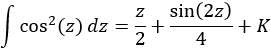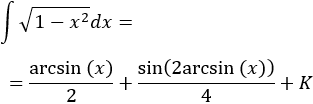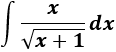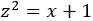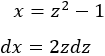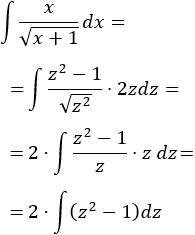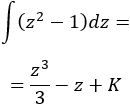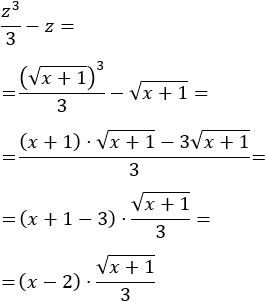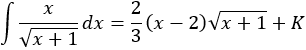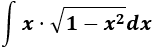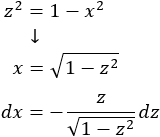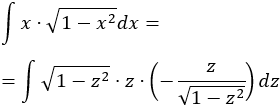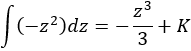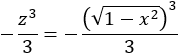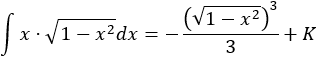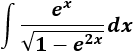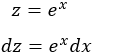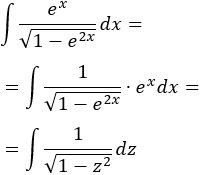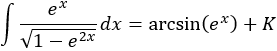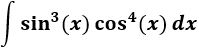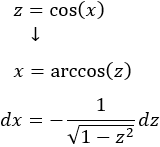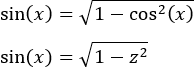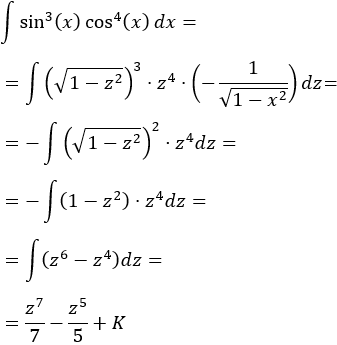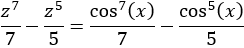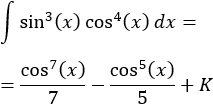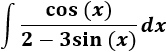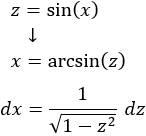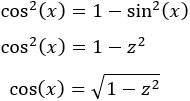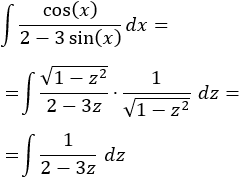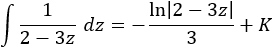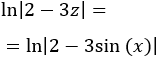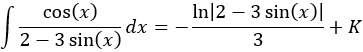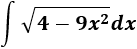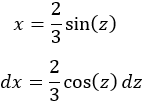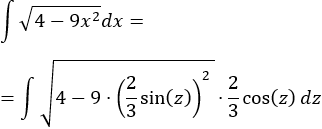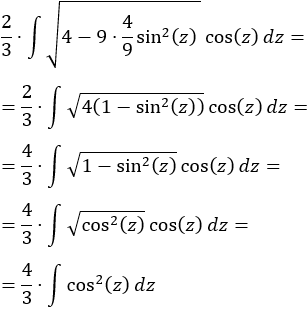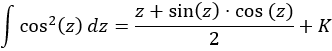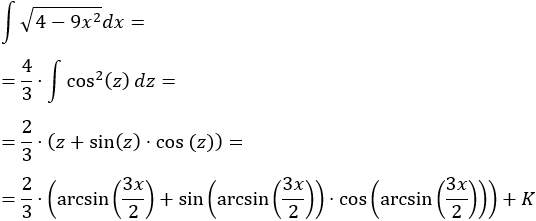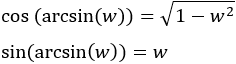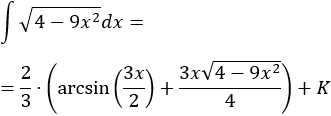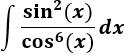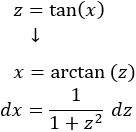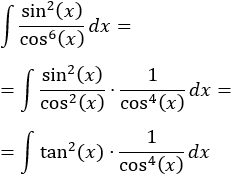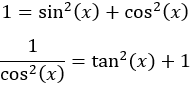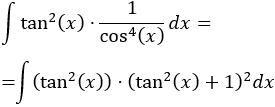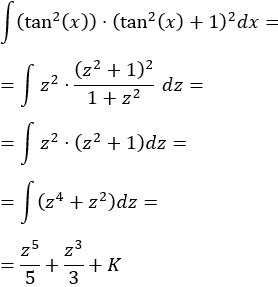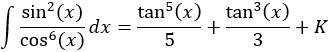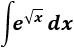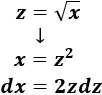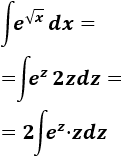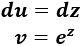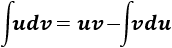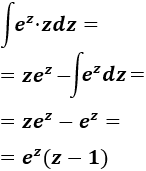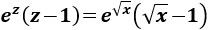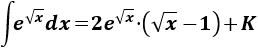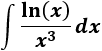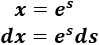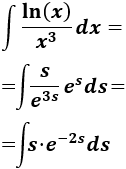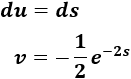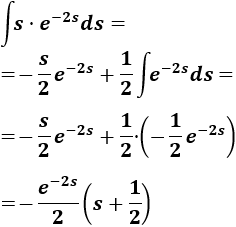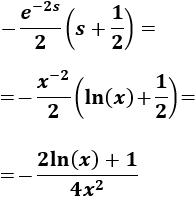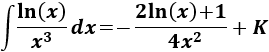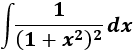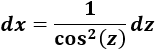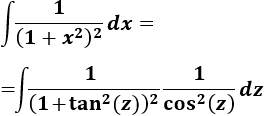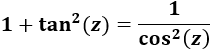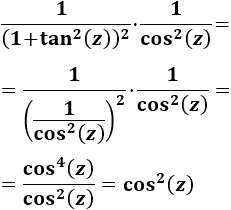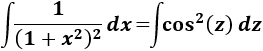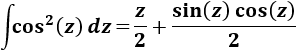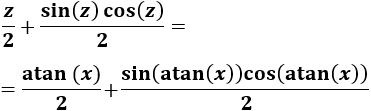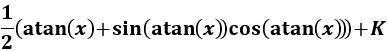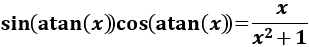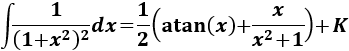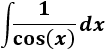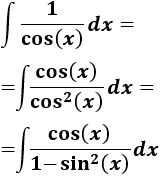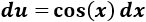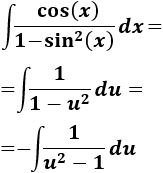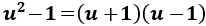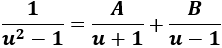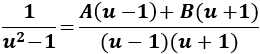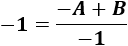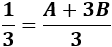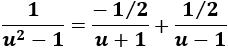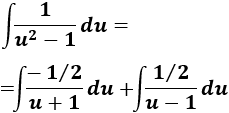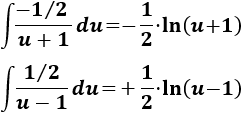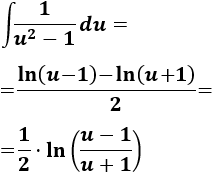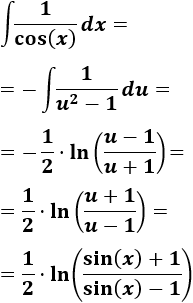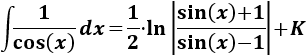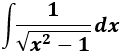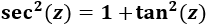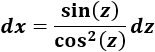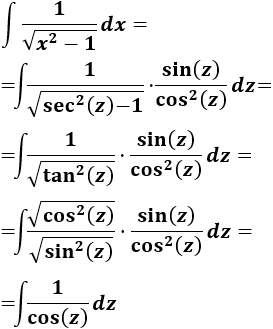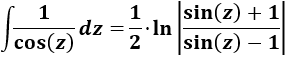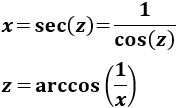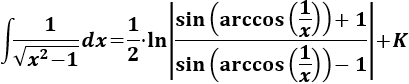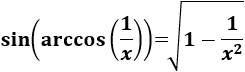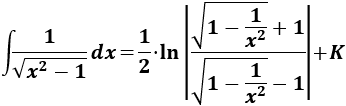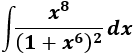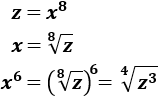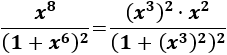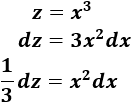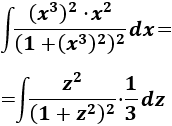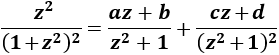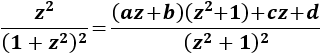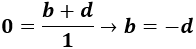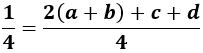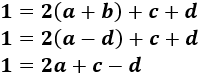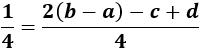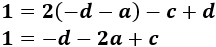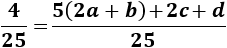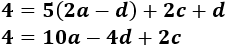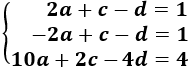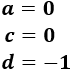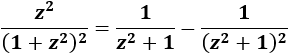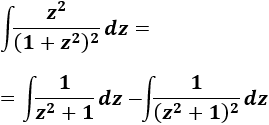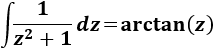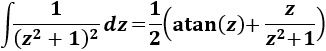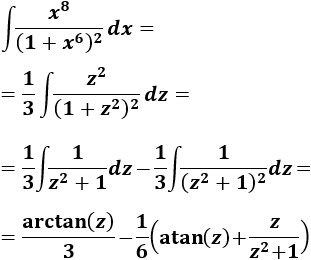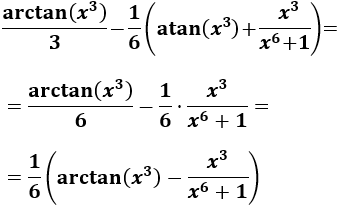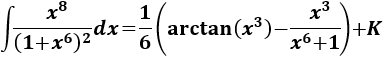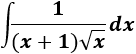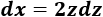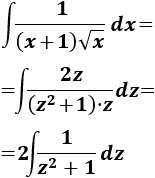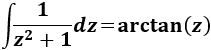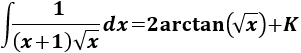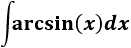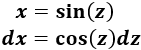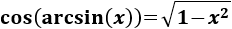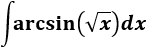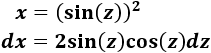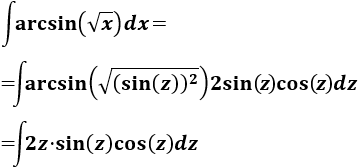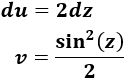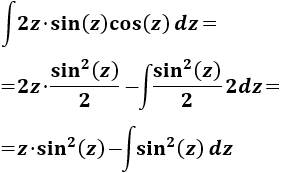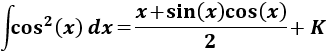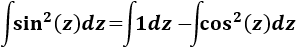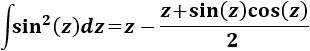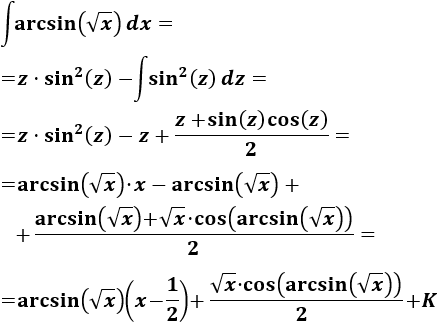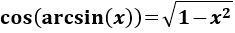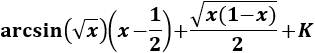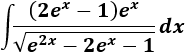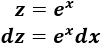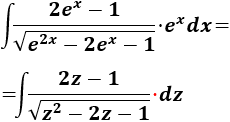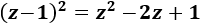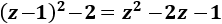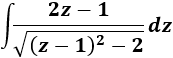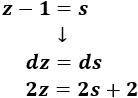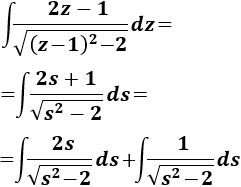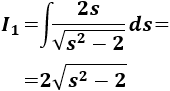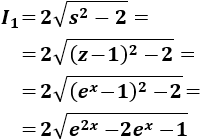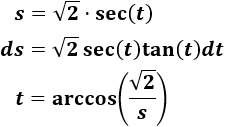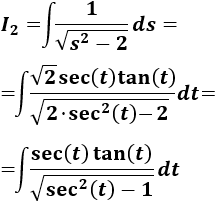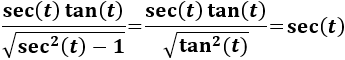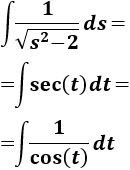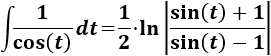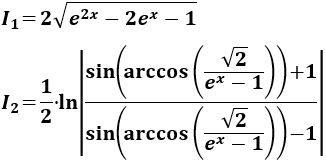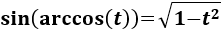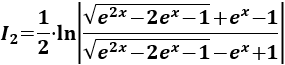Nota previa: en alguna de las integrales necesitaremos la primitiva del cuadrado del coseno:
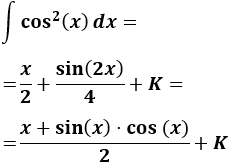
Integral 1 
Integral de un cociente con exponenciales:
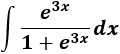
SOLUCIÓN
Atendiendo a la tabla, escogemos el cambio de variable
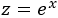
Con este cambio, \(e^{3x} = z^3\), así que obtendremos un cociente de polinomios.
Despejamos \(x\) aplicando logaritmos:
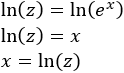
Derivamos para calcular \(dx\) (respecto de \(x\) en el lado izquierdo y respecto de \(z\) en el derecho):
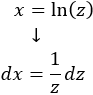
Sustituimos en la integral y simplificamos (no olvidéis sustituir también \(dx\)):
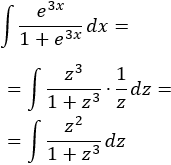
La integral obtenida es inmediata (un logaritmo):
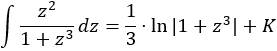
Deshacemos el cambio de variable:
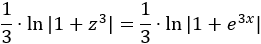
Por tanto,
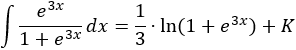
Nota: el valor absoluto ya no es necesario porque el argumento nunca es no positivo.
Integral 2 
Integral de un cociente con logaritmos naturales:
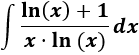
SOLUCIÓN
Como se indica en la tabla, escogemos el cambio
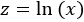
Despejamos \(x\) y derivamos:
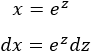
Sustituimos en la integral y simplificamos:
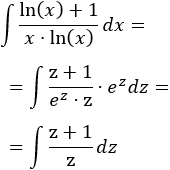
La integral que queda es inmediata, ya que podemos escribirla como una suma:
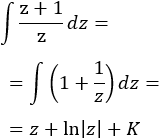
Deshaciendo el cambio, tenemos:
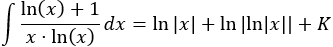
Integral 3 
Integral de una raíz cuadrada:
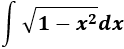
SOLUCIÓN
Teniendo en cuenta la tabla, escogemos el cambio
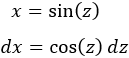
Sustituimos en la integral:
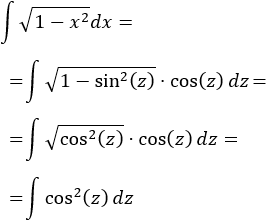
Como ya sabemos (lo recordamos en la nota previa), la integral del coseno al cuadrado es
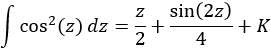
Deshaciendo el cambio de variable,
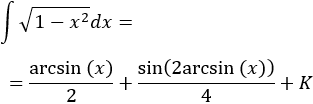
Nota: la razón de escoger el cambio \(x = \sin(z)\) cuando en el integrando tenemos \(\sqrt{1-x^2}\) es para aplicar la identidad fundamental \(1 - \sin^2(x) = \cos^2(x)\), con lo que se consigue eliminar el signo radical y así simplificar el integrando. Esto no significa que no podamos usar otro cambio de variable, ni que éste vaya a funcionar mejor o peor.
Integral 4 
Integral de un cociente con raíz cuadrada en el denominador:
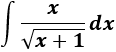
SOLUCIÓN
Escogemos el cambio de variable \(z^2\) igual al radicando para que desaparezca la raíz cuadrada (por estár al cuadrado). Luego sea
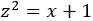
Despejamos \(x\) y derivamos:
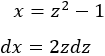
Sustituimos en la integral y simplificamos:
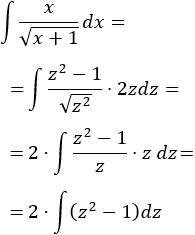
Calculamos la integral directa que queda:
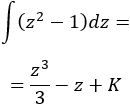
Deshacemos el cambio de variable:
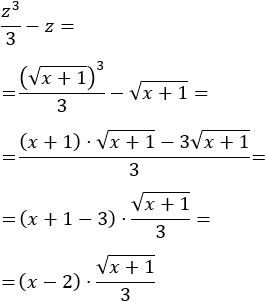
Por tanto,
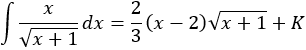
Integral 5 
Integral de un producto con raíz cuadrada:
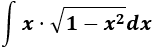
Nota: en realidad, esta integral es inmediata, pero la vamos a resolver por sustitución.
SOLUCIÓN
Escogemos un cambio de variable para eliminar la raíz:
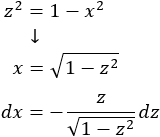
Sustituimos en la integral:
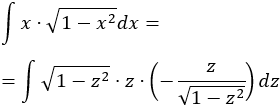
Simplificando, se obtiene la integral
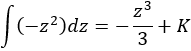
Deshacemos el cambio:
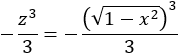
Por tanto,
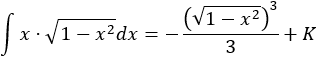
Integral 6 
Integral de un cociente con exponenciales y raíz cuadrada:
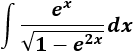
SOLUCIÓN
Vamos a resolver esta integral de forma un poco distinta a las anteriores (sin despejar \(x\)).
Atendiendo a la tabla, escogemos el cambio
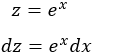
Aplicamos el cambio:
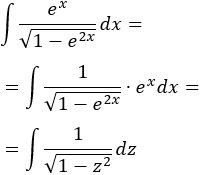
Observad que hemos cambiado directamente \(e^xdx\) por \(dz\).
La integral obtenida es directa por ser la derivada del arcoseno.
Por tanto, deshaciendo el cambio,
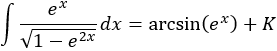
Integral 7 
Integral de un producto de potencias del seno y del coseno:
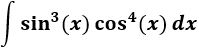
SOLUCIÓN
Como el exponente del seno es impar, utilizaremos el cambio
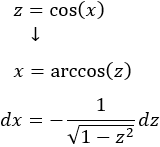
Escribimos el seno en función de la nueva variable:
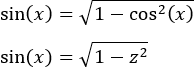
Aplicamos el cambio de variable:
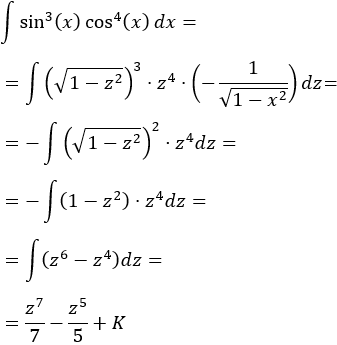
Deshacemos el cambio:
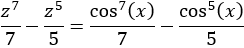
Por tanto,
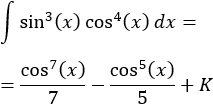
Integral 8 
Integral de un cociente de funciones trigonométricas:
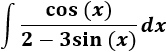
SOLUCIÓN
Tenemos un seno y un coseno en el integrando, pero como ambos tienen exponente impar, podemos escoger el cambio \(z=sin(x)\) ó \(z=cos(x)\). Elegimos el primero:
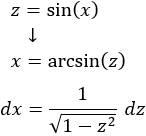
Necesitamos calcular el coseno de \(x\) en función de la nueva variable:
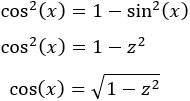
Sustituimos en la integral y simplificamos:
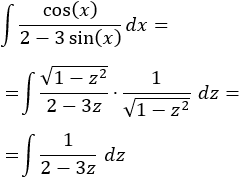
La integral obtenida es directa (un logaritmo):
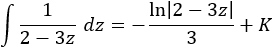
Deshacemos el cambio:
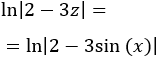
Por tanto,
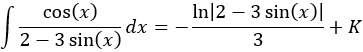
Integral 9 
Integral de una raíz cuadrada:
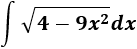
SOLUCIÓN
Atendiendo a la tabla, escogemos el cambio
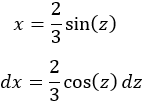
Aplicamos el cambio:
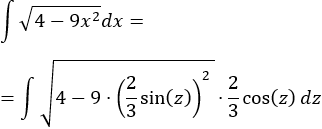
Simplificamos:
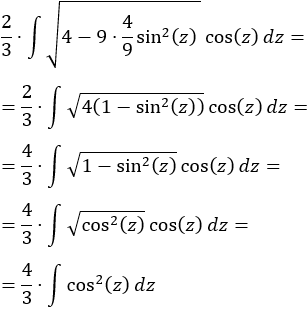
En la nota previa recordamos el resultado de la integral del cuadrado del coseno:
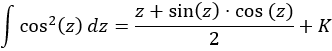
Por tanto, deshaciendo el cambio de variable,
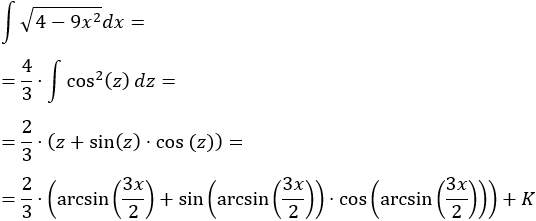
Podemos simplificar un poco el resultado teniendo en cuenta las siguientes identidades trigonométricas:
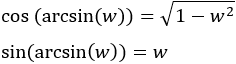
El resultado que obtenemos es
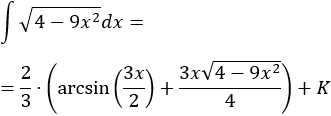
Integral 10 
Integral de un cociente de potencias de seno y del coseno:
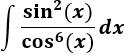
SOLUCIÓN
Según la tabla, como los exponentes son pares, escogemos el cambio
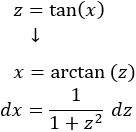
Como vamos a utilizar la tangente, reescribimos la integral:
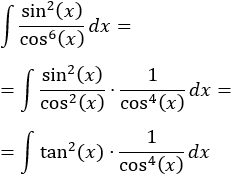
Si dividimos la identidad fundamental entre el coseno al cuadrado:
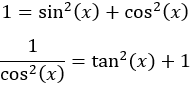
Continuamos simplificando:
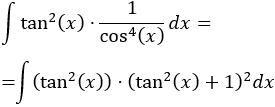
Aplicamos el cambio:
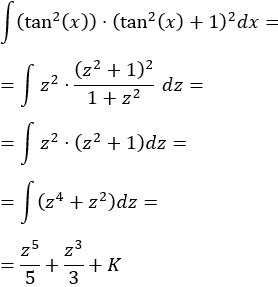
Por tanto, deshaciendo el cambio,
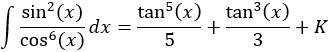
Integral 11 
Integral de exponencial:
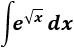
SOLUCIÓN
La integral de \(e^x\) es directa y la conocemos. Aplicaremos el cambio de variable \(z = \sqrt{x}\) para tener una integral parecida:
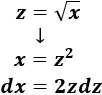
Aplicamos el cambio:
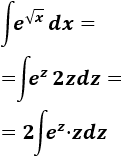
La dificultad de esta integral consiste en que debemos aplicar integración por partes. Sean \(u = z\) y \(dv = e^z dz\), entonces, derivando e integrando tenemos
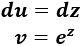
Recordamos la fórmula de integración por partes:
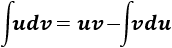
La aplicamos:
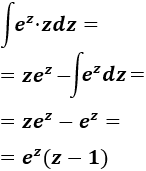
Deshacemos el cambio de variable:
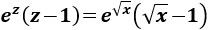
Por tanto, la integral inicial es
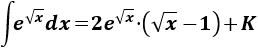
Nota: no olvidemos el 2 que sacamos inicialmente fuera de la integral.
Integral 12 
Integral de logaritmo entre potencia:
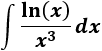
SOLUCIÓN
Consideremos el cambio de variable \(s = \ln(x)\), entonces:
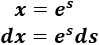
Sustituimos en la integral:
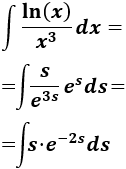
La integral es sencilla si aplicamos integración por partes.
Sean \(u = s\) y \(dv = e^{-2s}ds\). Entonces,
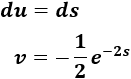
Aplicamos la fórmula:
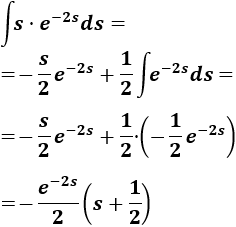
Deshacemos el cambio de variable:
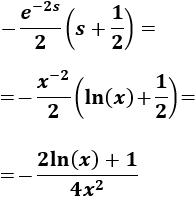
Por tanto,
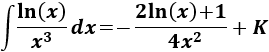
Integral 13 
Integral de función racional:
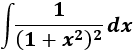
SOLUCIÓN
La tabla que vimos al inicio nos aconseja escoger el cambio \(x = \tan(z)\) cuando tenemos \(\sqrt(1+x^2)\). Usaremos este cambio aunque no tenemos la raíz cuadrada. Entonces,
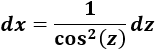
Aplicamos el cambio en la integral:
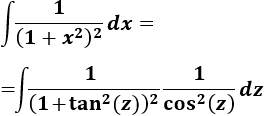
Ahora debemos recordar la siguiente identidad trigonométrica (demostrada en identidades trigonométricas):
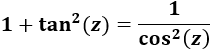
Operamos en el integrando:
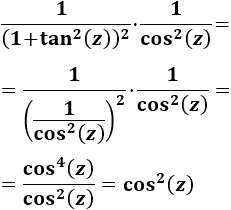
Por tanto, tenemos
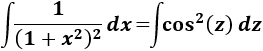
En la nota previa anterior a las integrales de esta página dimos el resultado de la última integral:
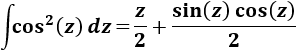
Deshacemos el cambio de variable:
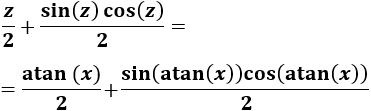
Luego el resultado de la integral inicial es
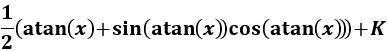
Nota: si operamos un poco (no es sencillo), podemos simplificar más el resultado:
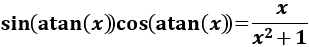
Con lo que la integral sería
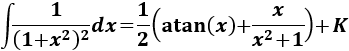
Integral 14 
Integral de secante:
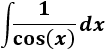
SOLUCIÓN
Podemos reescribir la integral:
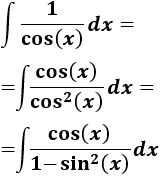
Consideremos el cambio de variable \(u = sin(x)\). Entonces,
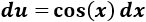
Lo aplicamos:
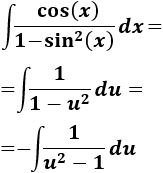
Observad que el polinomio del denominador es
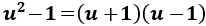
Luego por el teorema fundamental del álgebra podemos escribir
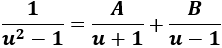
Sumamos las fracciones para hallar \(A\) y \(B\) dando valores a \(u\):
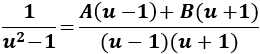
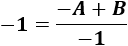
de donde \(A = B-1\).
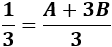
Resolviendo el sistema, tenemos \(A=-1/2\) y \(B = 1/2\), así que
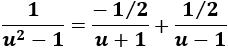
Luego tenemos
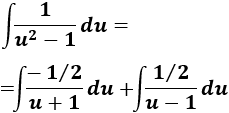
Estas integrales son directas:
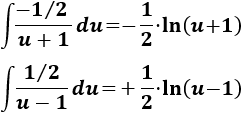
Por tanto,
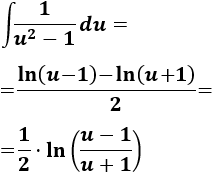
Volviendo atrás,
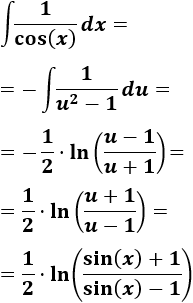
Por tanto,
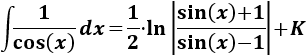
Integral 15 
Integral de función radical:
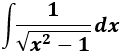
SOLUCIÓN
Recordamos una identidad trigonométrica básica:
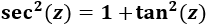
Podremos aplicar esta identidad si escogemos el cambio \(x = \sec(z)\):
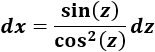
Aplicamos el cambio en la integral:
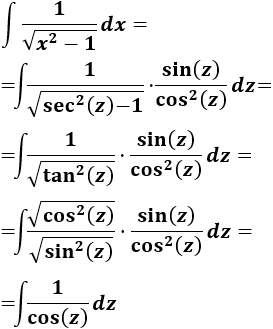
La integral resultante la hemos resuelto anteriormente:
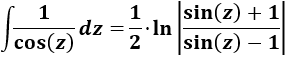
Deshacemos el cambio de variable:
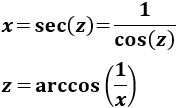
Por tanto,
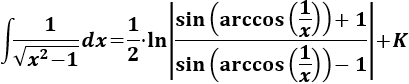
Nota: podemos usar la siguiente relación
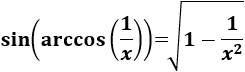
Entonces la integral quedaría como
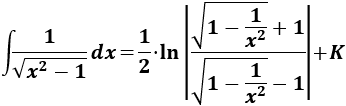
Integral 16 

Nota: esta integral es extremadamente difícil de resolver.
Integral de función racional:
SOLUCIÓN
Debemos escoger un cambio de variable del tipo \(z = x^n\). Ahora bien, determinar \(n\) para no complicar la integral no es fácil.
A modo de ejemplo, supongamos que escogemos \(z = x^6\). Lógicamente, al sustituir en el denominador no tenemos problema. Sin embargo, lo tenemos cuando queremos sustituir \(x^8\):
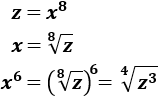
Por esta razón, primero vamos a reescribir el integrando:
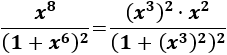
Ahora podemos considerar el cambio de variable \(z=x^3\) y veremos que sustituir \(x^2\) no será un problema porque es la derivada de \(x^3\).
Derivamos:
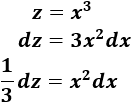
Aplicamos el cambio de variable en la integral:
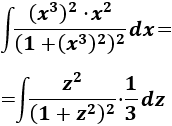
Esto nos ha permitido simplificar un poco el integrando, pero no lo suficiente. Tenemos la integral de una función racional con el grado del polinomio del denominador (4) mayor que el del numerador (2). Podemos aplicar el teorema fundamental del álgebra para escribir la fracción como una sumad de fracciones simples.
El polinomio del denominador es \((1+z^2)^2\), de cuya forma factorizada podemos deducir que tiene dos raíces complejas (conjugadas) de multiplicidad 2, luego podemos descomponer el integrando como sigue:
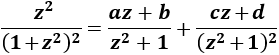
Para poder hallar las letras \(a\), \(b\), \(c\) y \(d\) sumamos las fracciones y damos valores a \(z\):
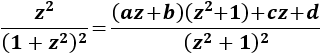
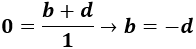
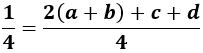
Entonces,
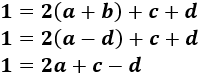
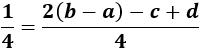
Entonces,
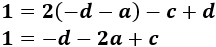
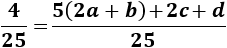
Entonces,
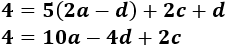
Luego tenemos un sistema de 3 ecuaciones y 3 incógnitas (\(a\), \(c\) y \(d\)):
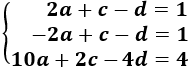
La solución del sistema anterior es (lo hemos resuelto por la regla de Cramer):
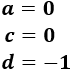
Y ya sabemos que \(b = -d = 1\).
Luego tenemos
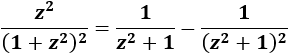
Por tanto,
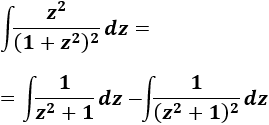
La primera integral es directa:
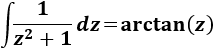
La segunda la hemos resuelto anteriormente (Integral 13):
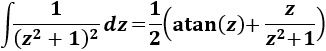
Por tanto, recapitulando, tenemos
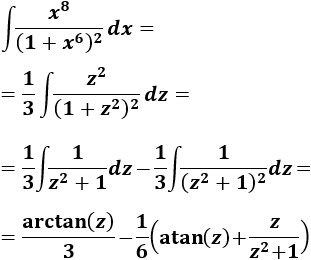
Luego, deshaciendo el cambio de variable (\(z = x^3\)), tenemos
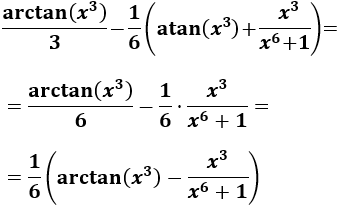
Por tanto, la integral inicial es
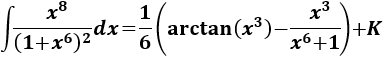
Integral 17 
Integral de cociente con raíz cuadrada:
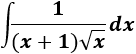
SOLUCIÓN
Sea \(x = z^2\), entonces
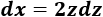
Aplicamos el cambio:
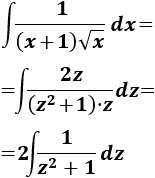
La integral que queda es directa:
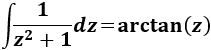
Deshacemos el cambio de variable:
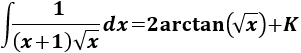
Integral 18 
Integral de arcoseno:
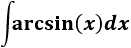
SOLUCIÓN
El cambio evidente que debemos escoger es
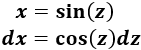
Lo aplicamos a la integral:
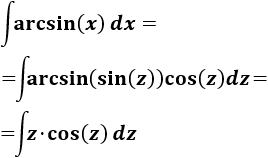
La integral que queda es sencilla si aplicamos integración por partes. Tomaremos \(u = z\) y \(dv = \cos(z)dz\), así que
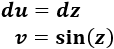
Aplicamos la fórmula:
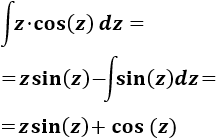
Finalmente, deshacemos el cambio de variable:
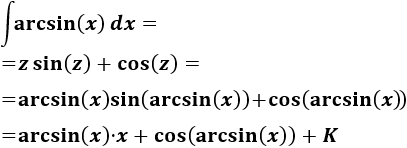
Nota: podemos también usar la relación
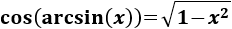
Integral 19 
Integral de arcoseno:
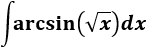
SOLUCIÓN
Esta integral se parece a la anterior y aplicaremos un cambio análogo:
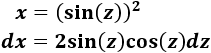
Aplicamos el cambio en la integral:
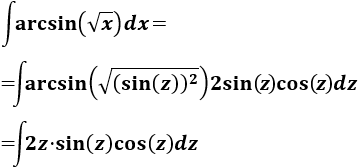
La integral que queda es fácil de resolver integrando por partes teniendo en cuenta que \(\sin(z)\cos(z)\) es (casi) la derivada de \(\sin^2(z)\).
Luego sean \(u = 2z\) y \(dv =\sin(z)\cos(z)\), entonces:
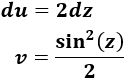
Aplicamos la fórmula:
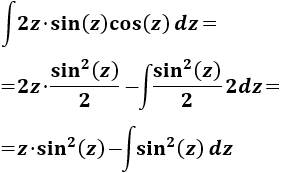
En la nota previa de las integrales proporcionamos la integral del coseno al cuadrado:
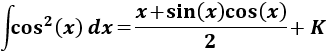
Luego, teniendo en cuenta la identidad trigonométrica fundamental,
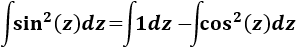
Por tanto,
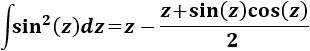
Por tanto, deshaciendo el cambio, tenemos que la integral inicial es
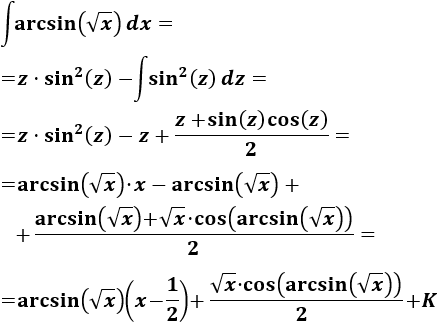
Nota: como ya hemos dicho anteriormente, podemos tener en cuenta que
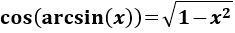
Por lo que podemos también escribir el resultado de la integral como
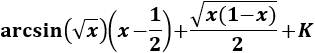
Integral 20 
Integral de cociente con exponenciales y raíz cuadrada:
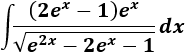
SOLUCIÓN
El cambio de variable más lógico es
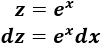
Aplicamos el cambio en la integral:
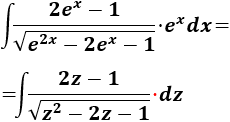
Nota: hemos escrito el punto multiplicativo justo antes de \(dz\) para que veamos claramente que hemos cambiado \(e^x dx\) por \(dz\).
Observemos que el cuadrado \((z-1)^2\) es casi el radicando:
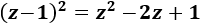
Por tanto, el radicando es
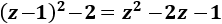
Y la integral podemos escribirla como
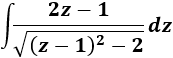
Consideramos ahora un nuevo cambio de variable:
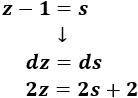
Aplicamos dicho cambio:
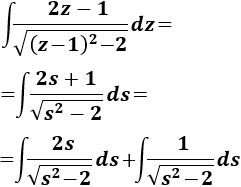
La primera integral es directa (derivada de una raíz):
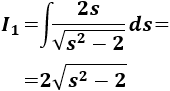
Deshacemos los cambios de variable:
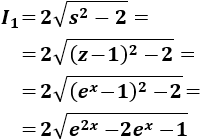
Para resolver la segunda integral tenemos que aplicar el cambio sugerido en la tabla de la introducción:
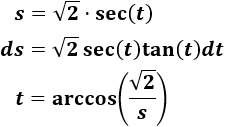
Aplicamos el cambio:
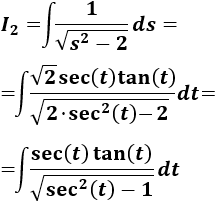
Ahora, teniendo en cuenta que \(\sec^2(t)-1 = \tan^2(t)\), el integrando queda como
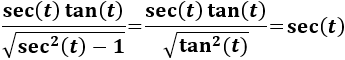
Luego
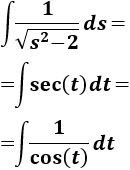
Esta última integral ya la hemos calculado anteriormente (Integral 14):
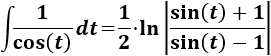
Deshacemos los cambios de variable:
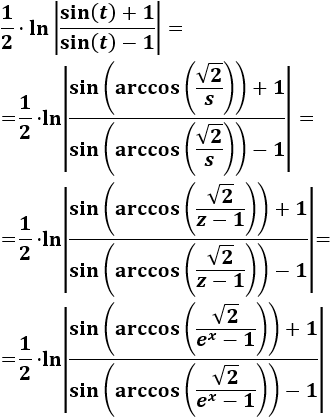
Entonces, la integral inicial es la suma de las integrales \(I_1\) e \(I_2\) (más la constante de integración):
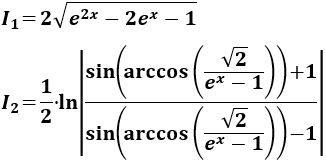
Nota: si tenemos en cuenta que
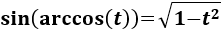
También podemos escribir \(I_2\) como
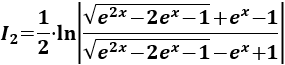
Páginas amigas: Problemas y Ecuaciones, Ecuaciones Resueltas.


Método de integración por sustitución o cambio de variable-
© -
matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.