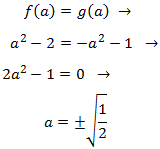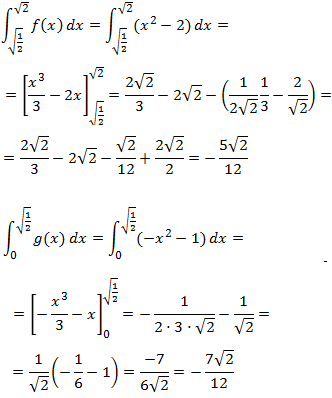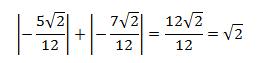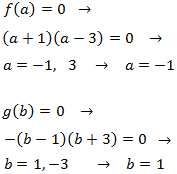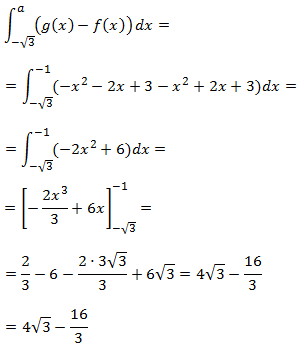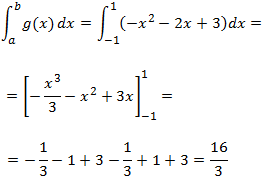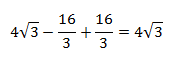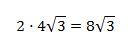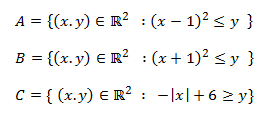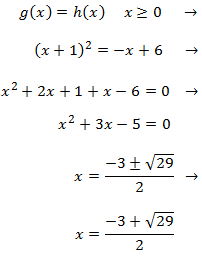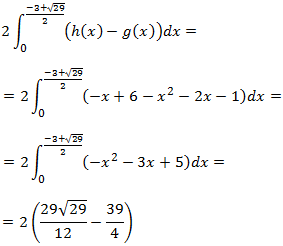En el Problema 10 y 11 se
calcula el área de un círculo y el área del interior de una
elipse, respectivamente,
considerando dichas áreas como las delimitadas por funciones.
En el Problema 15 y 16 se
calcula el área de una región no acotada
mediante el cálculo de una integral impropia de Riemann, cuyo
concepto se explica intuitivamente en su resolución.
En el Problema 17 se
calcula el área del conjunto intersección de tres conjuntos del plano
definidos analíticamente.
Problema 1
Calcular el área de la región
delimitada por la gráfica de la
función \(f(x) = x(x-2)\) y las
rectas verticales \(x^2 = 1\).
Solución
Las rectas verticales son
$$ x=-1,\ x = 1 $$
Como tenemos que integrar la función f, es mejor desarrollar el producto:
$$ f(x) = x(x-2) = x^2 -2x $$
Representamos la gráfica y las rectas para ver si
el eje horizontal divide la región:
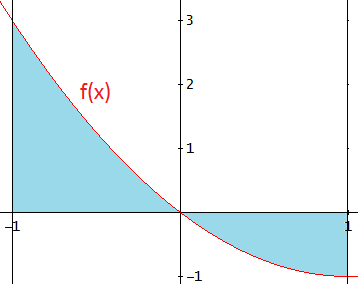
Como el eje OX divide la región en dos (una sobre el eje y otra bajo éste),
tenemos que calcular dos integrales. El resultado de la integral correspondiente
al área que está por debajo será negativo, por lo que tenemos que cambiar el
signo (o escribir el valor absoluto).
Los intervalos de x de las regiones son:
$$ [-1, 0],\ [0,1] $$
Nota: el extremo 0 se calcula resolviendo
la ecuación
$$ f(x) = 0 $$
Estos intervalos son los extremos de las integrales.
La integral indefinida de f es
$$ \int{f(x)}dx = \int{(x^2-2x)} dx =$$
$$ =\int{x^2}dx - \int{2x}dx = \frac{x^3}{3}-x^2$$
Calculamos las áreas calculando las integrales definidas mediante la regla de Barrow:
![calculamos las integrales definidas de x^2-2x en los intervalos [-1,0] y [1,0] integrales definidas: cálculo de áreas (regiones) del plano: ejercicios resueltos. Áreas entre gráficas de funciones. Introducción a la integral impropia de Riemann](https://www.matesfacil.com/primitivas/ReAr1-4.jpg)
El área es la suma del valor absoluto de los resultados obtenidos:
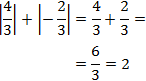
Por tanto, el área de la regón es 2.
Problema 2
Calcular el área de la región delimitada entre la gráfica de la función coseno, \(f(x) = cos(x)\), y las rectas verticales\(x = \pm \pi\).
Solución
Representamos la gráfica de f
y las dos rectas:
$$ x = -\pi, \ x = \pi $$
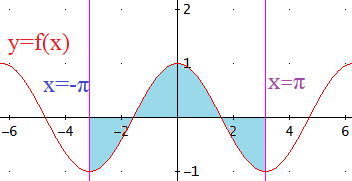
Tenemos tres regiones: una positiva (sobre el eje OX) y dos negativas (bajo el eje). Luego
debemos calcular tres integrales definidas.
Los intervalos de integración son
$$ \left[-\pi,-\frac{\pi}{2}\right],\ \left[-\frac{\pi}{2},\frac{\pi}{2}\right],\ \left[\frac{\pi}{2},\pi \right] $$
La integral indefinida de f es
$$ \int{f(x)} dx = \int{cos(x)}dx = sin(x) $$
Calculamos las integrales definidas en los tres intervalos:
![integrales definidas de cos(x) en los intervalos [-π,-π/2],[-π/2, π/2] y [π/2, π] integrales definidas: cálculo de áreas (regiones) del plano: ejercicios resueltos. Áreas entre gráficas de funciones. Introducción a la integral impropia de Riemann](https://www.matesfacil.com/primitivas/ReAr2-3.jpg)
Por tanto, el área total es
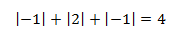
Nota:
Por la simetría de la función respecto del eje OY, podemos calcular
el área del primer cuadrante y multiplicarla por 2. También se puede
calcular el área de una de las regiones de longitud π/2 y
multiplicarla por 4.
Problema 3
Calcular el área de la región encerrada entre la gráfica de la
hipérbola \(f\)
y el eje de abscisas, siendo
$$ f(x) = \frac{1}{x}, \ 2\leq |x| \leq 3$$
Solución
La restricción sobre el dominio de la función nos proporciona las rectas verticales:
$$ 2\leq |x| \leq 3 \Rightarrow x \in [-3,-2]\cup [2,3]$$
Esto es lo mismo que decir que la región está compuesta por dos regiones, una delimitada por las dos rectas
$$ x = -3 ,\ x = -2 $$
y la otra por las dos rectas
$$ x = 3,\ x = 2 $$
Representamos las 4 rectas, la gráfica de f y la región cuya área vamos a calcular:
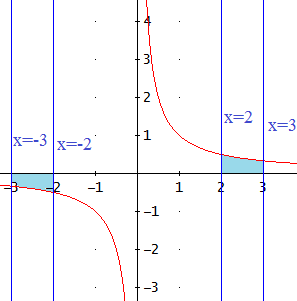
La integral indefinida de la función es
$$ \int{\frac{1}{x}}dx = ln|x| $$
Las integrales definidas en ambos intervalos son
$$ \int^3_2{\frac{1}{x}} dx = [ln|x|]^3_2 = ln(3) - ln(2) $$
$$ \int^{-2}_{-3}{\frac{1}{x}} dx = [ln|x|]^{-2}_{-3} = ln(2) - ln(3) $$
Por tanto, el área total es
$$ |ln(3) - ln(2)| + |ln(2) - ln(3)| =$$
$$ = ln\left(\frac{3}{2}\right)+\left|ln\left(\frac{2}{3}\right)\right| = $$
$$ = ln\left(\frac{3}{2}\right)+\left|-ln\left(\frac{3}{2}\right)\right| = $$
$$ = 2ln\left(\frac{3}{2}\right) = ln\left(\frac{9}{4}\right)$$
Problema 4
Calcular el área encerrada entre las gráficas de la recta y la parábola siguientes:
$$ f(x) = x $$
$$ g(x) = x^2 $$
Solución
Queremos calcular el área de la región azul:
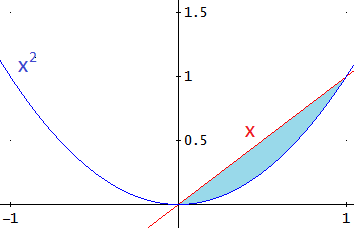
Como la región está sobre el eje de las abscisas, es suficiente calcular una única integral.
Antes de todo, calculamos los extremos de la integral. Estos extremos son los puntos donde intersectan ambas gráficas, es decir, las soluciones de la ecuación
$$f(x) = g(x) \rightarrow $$
$$ x= x^2 \rightarrow $$
$$ x(x-1) = 0 $$
Por tanto, los extremos son
$$ x = 1, 0 $$
Al calcular la integral de la función f obtenemos el área entre su gráfica y el eje horizontal (es una área mayor que
la azul). De forma análoga para la integral de g. Luego si se restan ambas áreas se obtiene el área de la región azul.
Por tanto, el área es
$$ \int^1_0{f(x)}dx - \int^1_{0}{g(x)}dx = $$
$$ = \int^1_0{x}dx - \int^1_{0}{x^2}dx = $$
$$ = \left[ \frac{x^2}{2}\right]^1_0 - \left[\frac{x^3}{3}\right]^1_0 = $$
$$ = \frac{1}{2} - \frac{1}{3} = \frac{1}{6} $$
Nota: como los resultados de ambas integrales son positivos (porque están sobre el eje OX), el área
puede calcularse directamente como
$$ \int^1_0{(f(x)-g(x))}dx $$
Problema 5
Calcular el área de la región
comprendida entre las gráficas de las parábolas
$$ f(x) = x^2 $$
$$ g(x) = -x^2 +2 $$
Solución
Representamos las gráficas de las funciones. Queremos
calcular el área de la región azul:
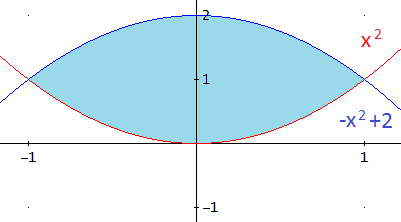
Como hay simetría, calcularemos el área de la mitad derecha de la región (primer cuadrante).
Además, como ambas funciones son no negativas en [-1, 1], calcularemos dicha área con una única integral (gráfica superior menos gráfica inferior):
$$ \int^1_0{(g(x)-f(x))}dx = $$
$$ = \int^1_0{(-x^2+2-x^2) }dx = $$
$$ = \int^1_0{(-2x^2 +2)} dx = $$
$$ = \left[ \frac{-2x^3}{3} +2x \right]^1_0 =$$
$$ = \frac{-2}{3} +2 = \frac{4}{3} $$
Por tanto, el área total de la región es el doble, es decir, 8/3.
Problema 6
Calcular el área de la región encerrada entre el eje horizontal y la función
$$ f(x) = x\cdot sin(x), \ 0\leq x \leq 2\pi $$
Solución
Queremos calcular el área de la región delimitada por la gráfica, el eje horizontal y las rectas x = 0 , x = 2π .
La región es la azul:
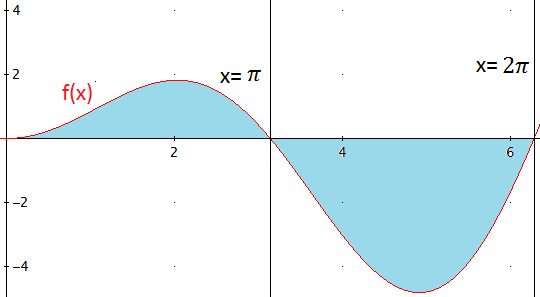
Nota: para representar la gráfica nos ayudamos de la gráfica del seno, pero como tiene el coeficiente x, la altura de los periodos aumenta a medida que aumenta |x|.
Buscamos el punto que divide ambos intervalos resolviendo la ecuación
$$ f(x)=0,\ x\in[0,2\pi] \rightarrow $$
$$ x\cdot sin(x) = 0,\ x\in[0,2\pi] \rightarrow $$
Las soluciones son
$$ x = 0, \pi, 2\pi$$
Pero el punto que nos interesa es x = π.
Calculamos la integral indefinida:
$$ \int{x\cdot sin(x)}dx$$
Aplicamos integración por partes:
$$ u = x \rightarrow du = 1 $$
$$ dv = sin(x) \rightarrow v = -cos(x) $$
Luego
$$ \int{x\cdot sin(x)}dx =$$
$$ = -x\cdot cos(x) + \int{cos(x)}dx =$$
$$ = -x\cdot cos(x) + sin(x)+C$$
Calculamos las integrales definidas en los dos intervalos:
$$ \int^{\pi}_{0}{x\cdot sin(x)}dx =$$
$$= [-x\cdot cos(x) + sin(x)]^{\pi}_{0} = \pi $$
$$ \int^{2\pi}_{\pi}{x\cdot sin(x)}dx = $$
$$= [-x\cdot cos(x) + sin(x)]^{2\pi}_{\pi} = $$
$$= -2\pi - \pi = -3\pi$$
El área total es la suma de los valores absolutos de los resultados
anteriores:
$$ |\pi |+|-3\pi| = 4\pi$$
Problema 7
Calcular el área encerrada entre el eje de las abscisas y la gráfica de la función definida
a trozos como
\[ f(x) = \begin{cases}
|x|, & \quad \text{si } 0 \leq |x| \leq 2 \\
0, & \quad \text{en otro caso}\\
\end{cases} \]
Solución
Representamos la gráfica de f (en rojo) y la región cuya área deseamos
calcular (azul):
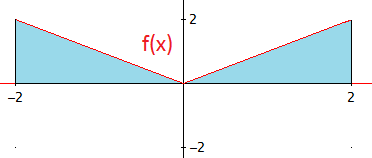
Como existe simetría respecto del eje de las ordenadas, será suficiente calcular el área de la mitad de la región y duplicarla. Calculamos el área de la mitad que se encuentra en el primer cuadrante, que se corresponde con la gráfica de la función f(x) = x .
La integral definida es
$$ \int^2_0{x}dx = \left[\frac{x^2}{2} \right]^2_0 = \frac{2^2}{2} = 2 $$
Por tanto, el área total es 4.
Problema 8
Calcular el área encerrada entre la gráfica de la función
polinómica de cuarto grado \(f\), el eje de las abscisas
y las rectas verticales \(x = 0\) y \(x = 7\):
$$ f(x) = x(x-1)(x-3)(x-6) $$
Solución
La forma factorizada en la que está escrita la función nos permite
representar su gráfica rápidamente ya que conocemos sus 4 raíces,
que son los puntos de corte con el eje de abscisas:
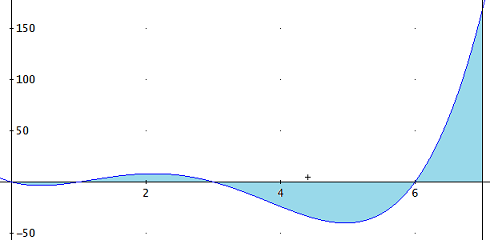
Hay 4 regiones: dos sobre el eje de abscisas y
dos bajo éste. Por tanto, tenemos que calcular cuatro integrales con el mismo
integrando pero en intervalos distintos.
Desarrollamos el producto de la función para facilitar el cálculo de la integral (indefinida):
$$ f(x) = x^4 -10x^3+27x^2-18x $$
Calculamos la integral indefinida de la función:
$$ \int{f(x)}dx =$$
$$= \int{x^4}dx -\int{10x^3}dx+ $$
$$ + \int{27x^2}dx-\int{18x}dx = $$
$$= \frac{x^5}{5} -\frac{10x^4}{4}+ $$
$$ + \frac{27x^3}{3}-\frac{18x^2}{2} = $$
$$ = \frac{x^5}{5} -\frac{5x^4}{2}+ 9x^3-9x^2 $$
Finalmente, calculamos las integrales definidas en cada intervalo. Los intervalos se obtienen fácilmente al conocer las raíces. Omitimos las operaciones por su sencillez:
$$ \int^{1}_{0}{f(x)}dx = -\frac{23}{10}$$
$$ \int^{3}_{1}{f(x)}dx = \frac{52}{5}$$
$$ \int^{6}_{3}{f(x)}dx = -\frac{729}{10}$$
$$ \int^{7}_{6}{f(x)}dx = \frac{697}{10}$$
Observad que los signos negativos corresponden a las regiones bajo el eje de abscisas.
Por tanto, el área total es
$$ |-\frac{23}{10}| + |\frac{52}{5}|+$$
$$
+ |-\frac{729}{10}| + |\frac{697}{10}| = \frac{1553}{10}$$
Problema 9
Calcular el área delimitada entre las gráficas de la
función valor absoluto, \(f(x) = |x|\), y la función cuadrado, \(g(x) = x^2\).
Solución
Ambas funciones son básicas y sus gráficas son:
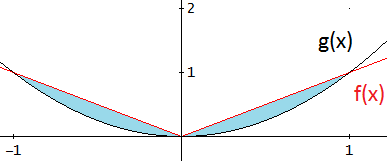
(queremos calcular el área de la región azul).
Como ambas funciones son pares, esto es, simétricas respecto del eje de las ordenadas, es suficiente calcular el área de la región del primer cuadrante y duplicarla.
Para obtener el intervalo de definición de la integral debemos calcular las intersecciones de las funciones, pero es inmediato que son los puntos x = 0 y x = 1.
Finalmente, como la gráfica de la función valor absoluto, f, está por encima de la de la función cuadrado g en dicho intervalo, el área viene dada por la integral
$$ \int^1_0{(f(x)-g(x))}dx = \int^1_0{f(x)}dx - \int^1_0{g(x)}dx =$$
$$ = \int^1_0{|x|}dx -\int^1_0{x^2}dx =$$
$$ = \left[\frac{x^2}{2}\right]^1_0-\left[\frac{x^3}{3}\right]^1_0 = $$
$$ = \frac{1}{2}-\frac{1}{3} = \frac{1}{6} $$
Nota: la primera de las integrales (con valor absoluto) es inmediata puesto que podemos eliminar el valor absoluto por ser el intervalo en los reales no negativos.
Por tanto, el área total es
$$ 2\cdot \frac{1}{6} = \frac{1}{3} $$
Problema 10 (dificultad alta)
Calcular analíticamente mediante integrales definidas el área de un círculo de radio 2.
Ayuda 1: la circunferencia de radio 2 (y centrada en el origen) está formada por los puntos \((x, y)\) del plano que cumplen la ecuación
$$ x^2 + y^2 = 4 $$
Ayuda 2:
$$ \int{cos^2(x)}dx = \frac{sin(x)cos(x)}{2} + \frac{x}{2} $$
$$ sin(arcsin(x))=x$$
$$ cos(arcsin(x)) = \sqrt{1-x^2} $$
Solución
De la ecuación de la circunferencia podemos despejar la y:
$$ x^2 + y^2 = 4 \rightarrow $$
$$ y = \pm \sqrt{4-x^2} $$
Consideremos las funciones
$$ f(x) = \sqrt{4-x^2} $$
$$ g(x) = -\sqrt{4-x^2} $$
Sus gráficas son las semicircunferencias superior e inferior.
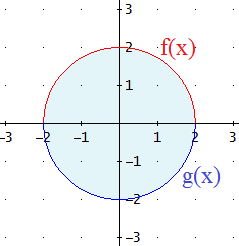
Observad que la integral de f en el intervalo [-2,2] proporciona el área de la mitad superior del círculo. Además, como f es una función par, la mitad de esta área es exactamente
$$ \int^2_0{f(x)}dx $$
Por tanto, al multiplicar por 4 el resultado de la integral anterior tendremos el área que buscamos.
La dificultad del problema radica en que la integral anterior no es inmediata. Para calcularla, aplicaremos el siguiente cambio de variable*:
$$ x = \sqrt{\frac{4}{1}}\cdot sin(t) = 2sin(t) $$
Nota*: aplicamos este cambio atendiendo a la tabla de cambios recomendables.
Derivamos en la expresión anterior:
$$ dx = 2cos(t) dt $$
Con lo que la integral (indefinida) queda como
$$ \int{\sqrt{4-x^2}}dx = \int{\sqrt{4-4sin^2(t)}2cos(t)}dt =$$
$$ = \int{\sqrt{4(1-sin^2(t))}2cos(t)}dt = $$
$$ = \int{\sqrt{4(cos^2(t))}2cos(t)}dt = $$
$$ = \int{2cos(t)2cos(t)}dt = $$
$$ = \int{4cos^2(t)}dt = $$
$$ = 4\int{cos^2(t)}dt =^* $$
$$ = 4\left( \frac{sin(t)cos(t)}{2} + \frac{t}{2}\right) =$$
$$ = 2sin(t)cos(t) + 2t$$
Para deshacer el cambio de variable tenemos que aislar t en
función de x:
$$ x = 2sin(t) \rightarrow t = arcsin\left(\frac{x}{2}\right) $$
Luego se obtiene
$$ 2 sin\left( arcsin\left(\frac{x}{2}\right) \right) cos\left( arcsin\left(\frac{x}{2}\right) \right) +2 arcsin\left(\frac{x}{2}\right) =$$
$$ =2\cdot \frac{x}{2} \cdot \left( \sqrt{1- \frac{x^2}{4}} \right) + 2arcsin\left(\frac{x}{2}\right) =$$
$$ =x\cdot \left( \sqrt{1- \frac{x^2}{4}} \right) + 2arcsin\left(\frac{x}{2}\right) =$$
$$ =\frac{x}{2}\cdot \left( \sqrt{4- x^2} \right) + 2arcsin\left(\frac{x}{2}\right) $$
Por tanto, la integral definida es
$$ \int^2_0{f(x)}dx =$$
$$ = \left[ \frac{x}{2}\cdot \left( \sqrt{4- x^2} \right) + 2arcsin\left(\frac{x}{2}\right) \right]^2_0 = $$
$$ = \pi -0 = \pi $$
Y el área del círculo de radio 2 es
$$ 4\cdot \pi $$
Problema 11 (dificultad alta)
Calcular analíticamente mediante integrales definidas el área de la región encerrada por la elipse
$$ \frac{x^2}{2} + \frac{y^2}{12} = 1 $$
Solución
De la ecuación obtenemos dos funciones despejando la y:
$$ f(x) = \sqrt{12\left(1-\frac{x^2}{2}\right)} $$
$$ g(x) = -\sqrt{12\left(1-\frac{x^2}{2}\right)} $$
El área que queremos calcular es la de la región azul:
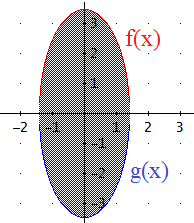
Buscamos los puntos de corte de la gráfica de f con el eje horizontal:
$$ f(x) = 0 \rightarrow $$
$$ x = \pm \sqrt{\frac{12}{6}} = \pm\sqrt{2} $$
Por las simetrías respecto de los ejes vertical y horizontal,
será suficiente calcular el área encerrada entre la gráfica de f y el eje horizontal en el primer cuadrante. Luego, la
multiplicaremos por 4.
Por tanto, el área de la elipse dada es
$$ 4\int^\sqrt{2}_0 {\sqrt{12-6x^2}}dx $$
Para calcular la integral aplicamos el cambio de variable
$$ x = \sqrt{2}sin(t)$$
Omitimos los cálculos por su similitud con el ejercicio anterior:
$$ \int {\sqrt{12-6x^2}}dx = $$
$$ = \sqrt{6}\cdot arcsin\left(\frac{x\sqrt{2}}{2}\right) + x\sqrt{6}\frac{\sqrt{2 - x^2}}{2} $$
Por tanto, el área total es
$$ 4\int^\sqrt{2}_0 {\sqrt{12-6x^2}}dx =$$
$$ = 4\cdot \frac{\pi \sqrt{6}}{2}= 2\pi \sqrt{6} $$
Problema 12
Calcular el área de la región que delimitan las gráficas de \(f\)
y de \(g\) y el eje de abscisas de modo que la
región sea adyacente al eje de las abscisas en el
intervalo formado por los dos puntos de corte de
la gráfica de \(f\) con dicho eje.
$$ f(x) = x^2-2 $$
$$ g(x) = -x^2 -1 $$
Solución
Lo primero que haremos es calcular los dos puntos de corte de f con el eje de abscisas:
$$ f(x) = 0 \rightarrow x^2-2=0 \rightarrow $$
$$ x = \pm \sqrt{2} $$
Por tanto, la región se encuentra entre las rectas
$$ x = \pm \sqrt{2} $$
y las gráficas de f y de g:
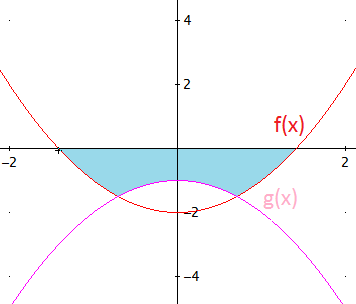
Observad que no podemos calcular el área con una sola integral. Es necesario calcular, al menos, dos integrales definidas. Nosotros lo haremos con dos, ayudándonos de la simetría respecto del eje vertical.
Como las funciones son simétricas respecto del eje de ordenadas, calcularemos el área de la región del cuarto cuadrante y la duplicaremos.
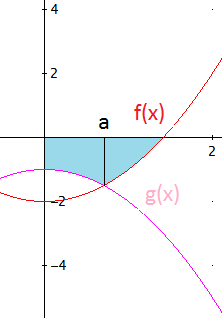
Ahora, dividimos la región en otras dos. Los intervalos para x de dicha división son:
![intervalo [0,a] y [a,raíz(2)] integrales definidas: cálculo de áreas (regiones) del plano: ejercicios resueltos. Áreas entre gráficas de funciones. Introducción a la integral impropia de Riemann](https://www.matesfacil.com/primitivas/ReAr12-3.jpg)
donde a es el punto en el que intersectan las funciones.
Esta división es importante porque en cada una de ellas, usaremos una u otra función en la integral.
Calcularemos el área que hay entre la gráfica de g y el eje en el primer intervalo y el área que hay entre la gráfica de f y el eje en el segundo.
Calculamos el punto a:
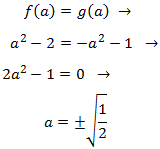
Nos quedaremos con el positivo, que es el que está en el semiplano derecho.
Y ahora ya sólo queda calcular las dos integrales definidas en cada intervalo
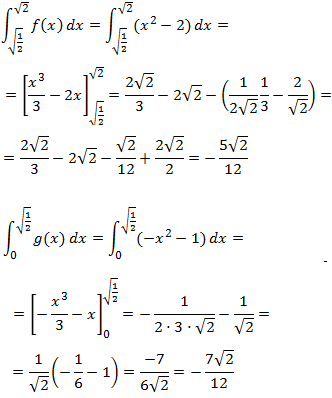
Por tanto, el área de la mitad de la región es
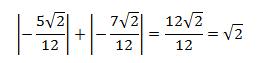
Con lo que el área total es \(2·\sqrt{2}\).
Problema 13
Calcular el área encerrada entre las gráficas de las funciones
\(f\) y \(g\):
$$ f(x) = (x+1)(x-3)$$
$$ g(x) = -(x-1)(x+3)$$
Solución
Como las funciones son polinómicas y de segundo grado, son parábolas. Nos ayudamos de la forma factorizada en la que están escritas para representar sus gráficas:
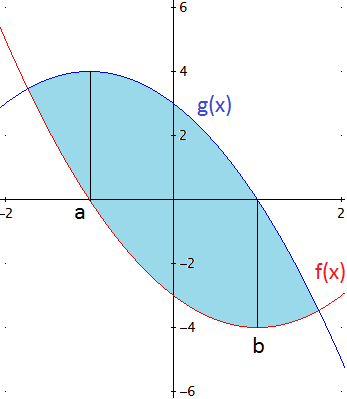
Desarrollamos los productos de las expresiones de las funciones para facilitar los cálculos de las integrales:
$$ f(x) = x^2 -2x -3 $$
$$ g(x) = -x^2 -2x+3 $$
En la representación de las gráficas se han representado también las rectas:
$$ x=a,\ x=b $$
Cada una de estas rectas pasa por uno de los puntos de
corte con de cada parábola con el eje de abscisas.
Los calculamos:
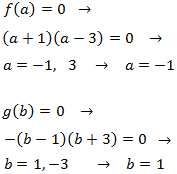
Hay simetrías, aunque a simple vista no podemos
asegurarlo. Por esta razón, resolvemos el problema, primero, sin considerar la simetría y, luego, considerándola. Es importante el procedimiento realizado en el primer caso.
Procedimiento sin considerar la simetría:
La región se encuentra dividida por el eje de las abscisas, por lo que tenemos que calcular las áreas de las partes superior e inferior por separado.
Las rectas anteriores (x = a y x = b)
dividen la región en otras tres:
De izquierda a derecha, el área de la primera región la proporciona la integral de g-f y, la tercera, el valor absoluto de la integral de f-g.
La región central la calculamos con otras dos integrales: la parte superior se corresponde con la integral de g y, la inferior, con el valor absoluto de la integral de f.
Obviamente, las cuatro integrales anteriores deben ser definidas en los correspondientes intervalos.
Buscamos los puntos de intersección entre las dos funciones:
$$ f(x) = g(x) \rightarrow $$
$$ x^2 -2x -3 = -x^2 -2x+3$$
Las soluciones de la ecuación de segundo grado son:
$$x = \pm \sqrt{3} $$
Por tanto, de izquierda a derecha, los intervalos son:
$$[-\sqrt{3},-1], [-1,1], [1, \sqrt{3}]$$
Las integrales definidas son:
$$ \int^{-1}_{-\sqrt{3}} {(g(x)-f(x))} dx = 4\sqrt{3} - \frac{16}{3} $$
$$ \int^{1}_{-1} {g(x)} dx = \frac{16}{3}$$
$$ \int^{1}_{-1} {|f(x)|} dx = \left|-\frac{16}{3}\right|$$
$$ \int^{\sqrt{3}}_{1} {|f(x)-g(x)|} dx = \left|\frac{16}{3}-4\sqrt{3}\right| $$
Por tanto, el área total es
$$ 4\sqrt{3} - \frac{16}{3}+ 2\cdot \frac{16}{3} -\left(\frac{16}{3}-4\sqrt{3}\right) =$$
$$ = 4\sqrt{3} + 4\sqrt{3} = 8\sqrt{3}$$
Procedimiento considerando la simetría:
El área de la región azul sobre el eje de las abscisas es la misma que el área de la región que está bajo éste. Por tanto, es suficiente calcular el área de la superior y duplicarla.
Sin embargo, como hemos dicho, la simetría no es tan evidente y, por tanto, para poder resolver el problema de este modo tenemos que demostrar la simetría. Si rotamos la parte inferior 180 grados respecto del origen, entonces obtenemos la región superior. Dicha rotación es equivalente a una simetría respecto del eje de abscisas junto con una simetría respecto del de ordenadas. Esto se consigue simplemente cambiando el signo de las dos coordenadas de cada punto.
Al rotar el punto
$$ b = (-\sqrt{3},0) $$
obtenemos el punto
$$ (\sqrt{3}, 0) = a $$
Y la rotación de la gráfica de f, es decir, el conjunto de puntos
$$ (x,f(x)) $$
es el conjunto de puntos
$$ (-x, -f(x)) $$
Pero observad que
$$ -f(x) = -x^2 +2x +3 $$
$$ g(-x) = -(-x)^2 -2(-x)+3 =$$
$$= -x^2 +2x +3 =-f(x) $$
Luego
$$ (-x,-f(x)) = (-x, g(-x))$$
que es precisamente la gráfica de g.
Calculamos el área de la región superior:
Dividimos la región en otras dos con la recta x = a:
En la primera, tenemos que calcular el área que hay entre las dos gráficas:
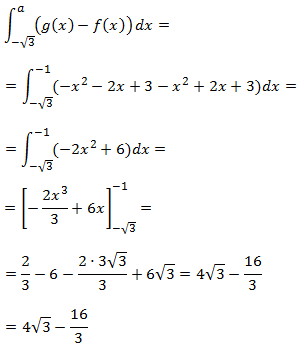
En la segunda, tenemos que calcular el área encerrada bajo la gráfica de g:
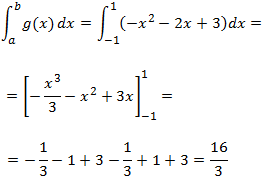
Por tanto, el área de la parte superior es
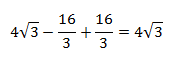
Y el área total es
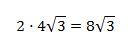
Problema 14
Calcular el área encerrada entre las gráficas de las siguientes funciones (valor absoluto y parábola):
$$ f(x) = |x^2 -3| $$
$$ g(x) = 2x^2+1 $$
Solución
Es más cómodo escribir f como una función definida a trozos en lugar de un valor absoluto. Pero para ello necesitamos saber cuándo cambia el signo del argumento del valor absoluto:
$$ x^2-3 = 0 \leftarrow x = \pm \sqrt{3}$$
Por tanto, la función es
$$ f(x) = \begin{cases}
-x^2+3, & \quad \text{si } |x| \leq \sqrt{3} \\
x^2-3, & \quad \text{en otro caso}\\ \end{cases} $$
La representación de las gráficas y de la región que encierran es:
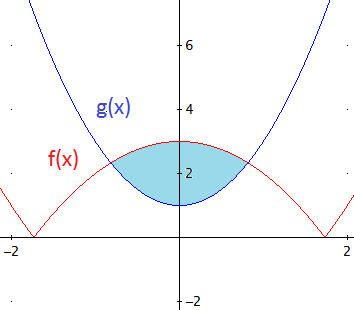
Buscamos los puntos de intersección de las funciones:
$$ f(x) = g(x), \ x\in [-\sqrt{3}, \sqrt{3}] \rightarrow $$
$$ -x^2+3 = 2x^2 +1 \rightarrow x= \pm \sqrt{\frac{2}{3}} $$
Como la región está en el semiplano superior, el área viene dada por la integral definida de f - g (superior menos inferior). Usaremos también que existe simetría respecto del eje de las ordenadas:
$$ \int^{\sqrt{\frac{2}{3}}}_{0}{(f(x)-g(x))}dx = $$
$$= \int^{\sqrt{\frac{2}{3}}}_{0}{(-x^2+3-2x^2-1)}dx = $$
$$= \int^{\sqrt{\frac{2}{3}}}_{0}{(-3x^2+2)}dx = \frac{4\sqrt{6}}{9}$$
Por tanto, el área total es
$$\frac{8\sqrt{6}}{9}$$
Problema 15 (dificultad alta)
Región con área infinita (es una integral impropia de Riemann)
Calcular el área de la región de longitud infinita
delimitada por la gráfica de la función
$$ f(x) = \frac{1}{x^2}$$
y el eje de las abscisas en el intervalo de los reales mayores que 1.
Solución
La representación de la gráfica y de la región es:
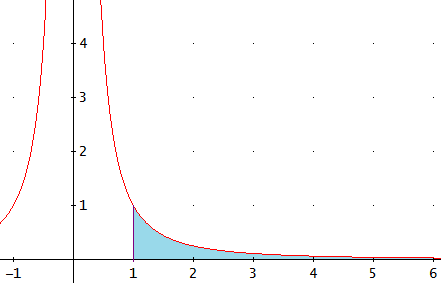
Observad que la longitud (eje horizontal) de la región es infinita pero, sin embargo, veremos que su área es finita.
Según el razonamiento de los problemas anteriores, el área de la región la proporciona la integral definida en el intervalo de los reales mayores que 1, es decir, con un extremo infinito:
$$ \int^{+\infty}_{1}{ f(x)}dx $$
Esta integral se denomina impropia de Riemann y se calcula del siguiente modo:
- Se cambia el extremo (o los extremos) infinito por
un parámetro (por ejemplo, u).
- Se calcula la integral definida en el nuevo intervalo.
- Se calcula el límite cuando el parámetro (o parámetros) tiende
al extremo infinito.
Resolvemos la integral del problema:
$$ \int^{+\infty}_{1}{ f(x)}dx =$$
$$ = \lim_{u\to +\infty} \left( \int^{u}_{1}{ \frac{1}{x^2}}dx \right) = $$
$$ = \lim_{u\to +\infty} \left[ -\frac{1}{x}\right]^{u}_1 = $$
$$ = \lim_{u\to +\infty} \left( 1-\frac{1}{u} \right) = 1$$
Por tanto, el área de la región (con longitud infinita) es 1 (finita).
Problema 16 (dificultad alta)
Región con área infinita (es una integral impropia de Riemann)
Calcular el área encerrada entre la gráfica de la función exponencial
$$ f(x) = e^x $$
y el eje de abscisas en el intervalo de los reales menores que 1.
Solución
La región cuya área buscamos es la azul:
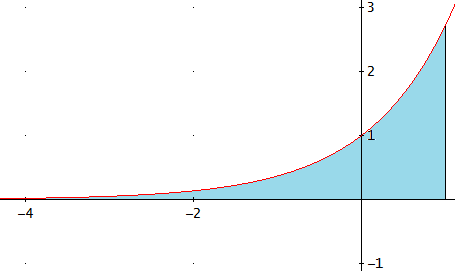
De forma análoga al problema anterior, el área viene dada por la integral impropia de Riemann
$$ \int^1_{-\infty}{e^x }dx $$
La resolvemos:
$$ \int^1_{-\infty}{e^x }dx = $$
$$ = \lim_{u\to -\infty} \left( \int^1_{u}{e^x }dx \right) = $$
$$ = \lim_{u\to -\infty} \left[ e^x \right]^1_{u} = $$
$$ = \lim_{u\to -\infty} ( e - e^u ) = e$$
Por tanto, el área total de la región es el número e.
Problema 17
Calcular el área de la región determinada por la intersección de los siguientes conjuntos del plano:
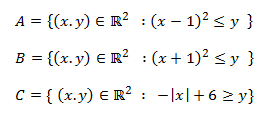
Solución
Representamos los conjuntos para determinar la región:
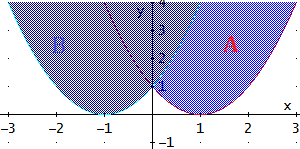
Conjunto A:
Los puntos que cumplen la igualdad son los de la gráfica de la función
$$ f(x) = (x-1)^2 $$
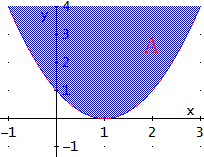
Los puntos del conjunto A son los que están por encima de su gráfica.
Conjunto B:
Los puntos que cumplen la igualdad son los de la gráfica
de la función
$$ g(x) = (x+1)^2 $$
Los puntos del conjunto B son los que están por encima de su gráfica.
Conjunto C:
Nos ayudamos de la gráfica de la función definida a trozos
\[ h(x) = \begin{cases}
-x+6, & \quad \text{si } 0 \leq x \\
x+6, & \quad \text{en otro caso}\\
\end{cases} \]
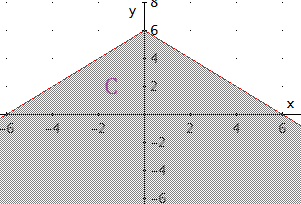
Los puntos del conjunto C son los que están por debajo de la gráfica.
Intersectamos los tres conjuntos y obtenemos la región (azul):
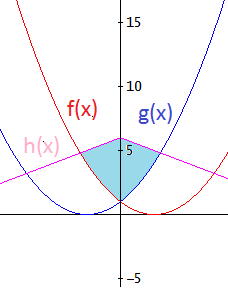
La función h es simétrica respecto del eje vertical; las otras dos gráficas (que son la misma función pero desplazadas), también lo son.
Calcularemos el área de la parte de la región que está en el primer cuadrante y la duplicaremos. Para calcularla, sólo necesitamos las funciones g y h .
Calculamos el punto de intersección de ambas gráficas g y h:
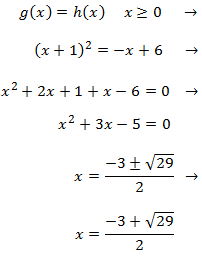
Nota: sólo el valor escogido (signo positivo) es el punto de corte buscado. Para calcular el otro punto (en el segundo cuadrante), hay que tener en cuenta que cambia la definición de h .
El área total es el doble del área de la región del primer cuadrante, es decir, el área es
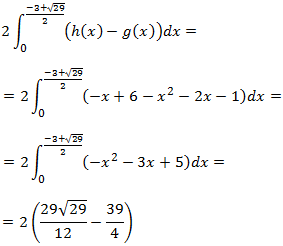


Integral definida: cálculo de áreas - © matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.

![representación de la gráfica de una función poitiva
F(x) y de la región que encierra junto con el
eje de abscisas en el intervalo [a,b] integrales definidas: cálculo de áreas (regiones) del plano: ejercicios resueltos](primitivas/IntArea1.png)
![representación de la gráfica de una función negativa
F(x) y de la región que encierra junto con el
eje de abscisas en el intervalo [a,b] integrales definidas: cálculo de áreas (regiones) del plano: ejercicios resueltos](primitivas/IntArea2.png)
![representación de la gráfica de una función positiva y negativa
F(x) y de la región que encierra junto con el
eje de abscisas en el intervalo [a,c] integrales definidas: cálculo de áreas (regiones) del plano: ejercicios resueltos](primitivas/IntArea3.png)
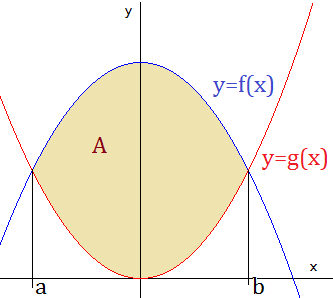

![calculamos las integrales definidas de x^2-2x en los intervalos [-1,0] y [1,0] integrales definidas: cálculo de áreas (regiones) del plano: ejercicios resueltos. Áreas entre gráficas de funciones. Introducción a la integral impropia de Riemann](https://www.matesfacil.com/primitivas/ReAr1-4.jpg)
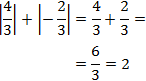

![integrales definidas de cos(x) en los intervalos [-π,-π/2],[-π/2, π/2] y [π/2, π] integrales definidas: cálculo de áreas (regiones) del plano: ejercicios resueltos. Áreas entre gráficas de funciones. Introducción a la integral impropia de Riemann](https://www.matesfacil.com/primitivas/ReAr2-3.jpg)
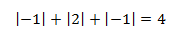











![intervalo [0,a] y [a,raíz(2)] integrales definidas: cálculo de áreas (regiones) del plano: ejercicios resueltos. Áreas entre gráficas de funciones. Introducción a la integral impropia de Riemann](https://www.matesfacil.com/primitivas/ReAr12-3.jpg)