7. Espacio de Hausdorff, T₂

Definición 7.1.

Un espacio topológico \( (X, \mathcal{T}) \) es de Hausdorff o \( T_2 \) si para cada par de puntos distintos existen dos abiertos \( A,B \in\mathcal{T}\) disjuntos tales que \( x\in A\) e \( y\in B \).

Ejemplo 1:

El espacio topológico de los reales con la topología usual, \( (\mathbb{R}, \mathcal{T}_u) \), es de Hausdorff:

Sean \( x\) e \( y\) dos puntos distintos de \( \mathbb{R}\).

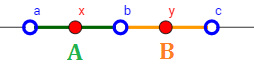
Podemos suponer que \( x < y \). Entonces, existen tres reales \( a\), \( b\) y \( c\) tales que

$$ a< x < b < y < c $$

Los conjuntos

$$ A = (a,b) $$

$$ B = (b,c) $$

son abiertos por ser intervalos abiertos. Además, son disjuntos cumpliendo \( x\in A\) e \( y\in B \).

Ejemplo 2:

El espacio topológico del plano real con la topología usual, \( (\mathbb{R}^2, \mathcal{T}_u) \), es de Hausdorff:

La topología usual es la inducida por la distancia euclídea

$$ d((x_1,x_2),(y_1,y_2)) = \sqrt{\sum_{i=1}^2(x_i-y_i)^2} $$

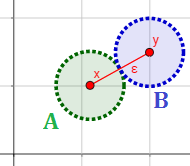
Dados dos puntos distintos \( x\) e \( y\) de \( \mathbb{R}^2\), sea \( \varepsilon = \frac{d(x,y)}{2} \).

Entonces, los conjuntos

$$ A = B_d(x, \varepsilon ) $$

$$ B = B_d(y, \varepsilon ) $$

son abiertos por ser las bolas abiertas asociadas a la distancia \( d \).

Estas discos son disjuntos con \( x\in A\) e \( y \in B\).

Ejemplo 3:

El espacio de Sierpinski \( (\{ 0, 1\}, \mathcal{T}_{Si} )\) cuya topología es

$$ \mathcal{T}_{Si} = \{ \emptyset, \{ 1 \} , \{ 0,1 \} \} $$

no es de Hausdorff:

Los únicos abiertos a los que pertenece 1 son

$$ \{ 1 \}, \{ 0, 1 \} $$

El único abierto al que 0 pertenece es

$$ \{ 0,1\} $$

Por tanto, no existen abiertos disjuntos (excepto el conjunto vacío).

Nota 1: vimos que este espacio es de Kolmogórov (\( T_0 \)) y no es de Fréchet (\( T_1 \)). Esto es suficiente para demostrar que tampoco es de Hausdorff (\( T_2 \)) ya que, como veremos a continuación, (\( T_2 \rightarrow T_1 \)).

Nota 2: también veremos que todo espacio métrico es de Hausdorff.

Teorema 7.1.

Un espacio topológico \( (X, \mathcal{T}) \) de Hausdorff es también de Fréchet. Es decir, \( T_2 \rightarrow T_1\).

Nota 1: una consecuencia directa de este resultado es que el espacio es también de Kolmogórov (\(T_0\)) puesto que \( T_1 \rightarrow T_0 \).

Nota 2: otra consecuencia es que en un espacio de Hausdorff el conjunto \(\{x\}\) es cerrado \( \forall x\in X\) por una caracterización de los espacios de Fréchet (\(T_1\)).

Teorema 7.2.

En un espacio topológico \( (X, \mathcal{T}) \) de Hausdorff, las sucesiones convergentes convergen a un único punto.

Nota: una sucesión \( \{x_n\}_{n\in\mathbb{N}}\) es convergente a \( x\in X\) si para cada entorno de \( x\), \( E\in\mathcal{E}(x)\), existe un natural \(n_0 \) tal que \( x_n \in E, \forall n\geq n_0\).

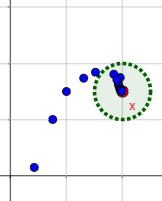
Nota 2: puesto que todo entorno \(E\) de \(x\) contiene a algún abierto \( A\) tal que \( x \in A\), en la definición de convergencia podemos cambiar el entorno \(E\) de \(x\) por el abierto \(A\).

Teorema 7.3.

Los subespacios de un espacio topológico \( (X, \mathcal{T}) \) de Hausdorff son también de Hausdorff.

Nota: sea \(S \subseteq X\) un subconjunto de \(X\), se llama subespacio topológico al espacio \(( S, \mathcal{T}_S)\) siendo \( \mathcal{T}_S\) la topología

$$ \mathcal{T}_S :=\{ A\cap S: A\in \mathcal{T}\} $$

Teorema 7.4.

Todo espacio métrico \( (X, d )\) es un espacio topológico de Hausdorff.