Andrey Kolmogórov y los axiomas y espacios de Kolmogórov
En esta página proporcionamos una breve biografía del matemático Andrey Kolmogórov y sus axiomas. También, definimos espacio topológico de Kolmogórov y demostramos que todo espacio de Hausdorff es también de Kolmogórov. Se incluyen ejemplos.
Contenido de esta página:
- Biografía de Andrey Kolmogórov
- Axiomas de Kolmogórov
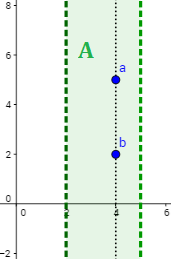
- Espacios topológicos de Kolmogórov o \(T_0\)
Páginas relacionadas
Otras páginas:
1. Andrey Kolmogórov (1903-1987)
Andrey Nikolaevich Kolmogorov (1903-1987) fue un matemático y físico ruso con numerosas e importantes aportaciones en dichas ciencias. En 1920, ingresó en la Universidad Estatal de Moscú y en el Instituto Tecnológico de Química Mendeleev de Rusia. En este período demostró varios resultado de la teoría de conjuntos y de las series de Fourier. En 1939 fue nombrado miembro de la Academia de Ciencias de Rusia. También fue académico de la Royal Society, de la Real Academia de Artes y Ciencias de los Países Bajos y de la Academia de Ciencias de Francia.
Se le atribuye la siguiente cita [traducida al español]:
Todo matemático cree que está por encima de los otros. La razón por la que no lo anuncian en público es porque son inteligentes.
Algunos conceptos o resultados que llevan su nombre en su honor son:
- Ecuación de Fischer-Kolmogórov
- Axiomas de Kolmogórov
- Teorema de continuidad de Kolmogórov
- Teorema de Fréchet-Kolmogórov
- Teorema de superposición de Kolmogórov
- Espacio de Kolmogórov
- Paradoja de Borel-Kolmogórov