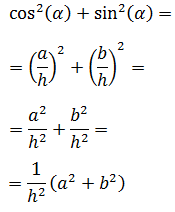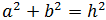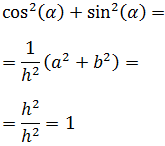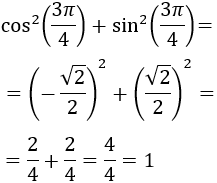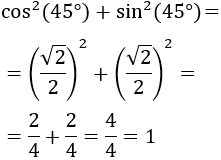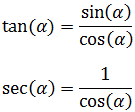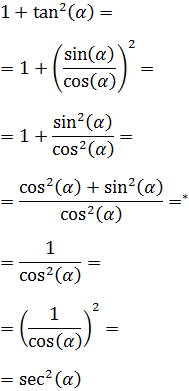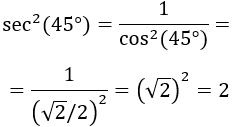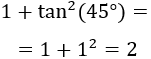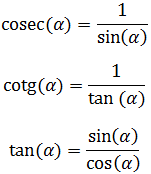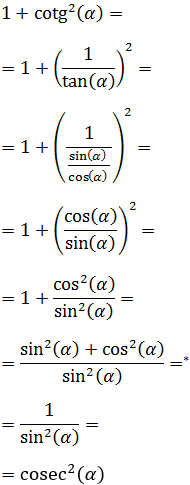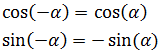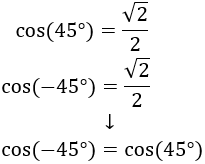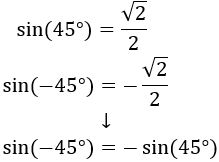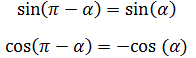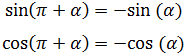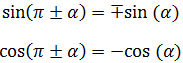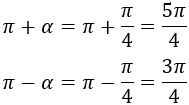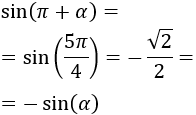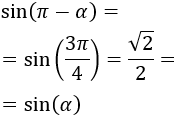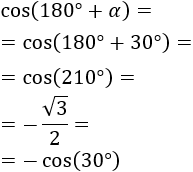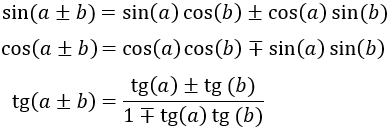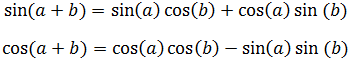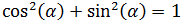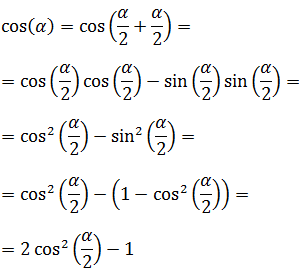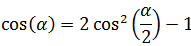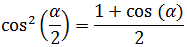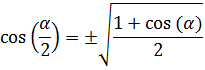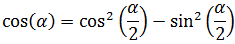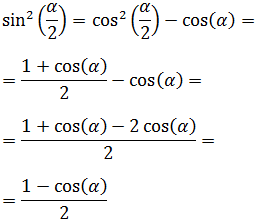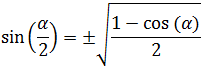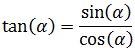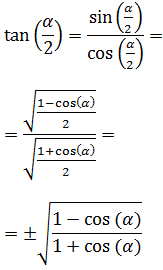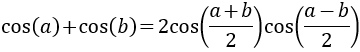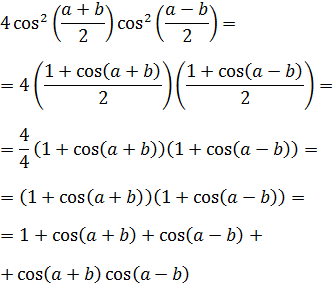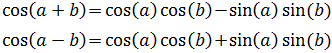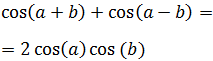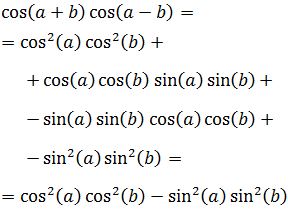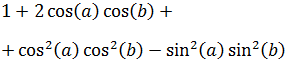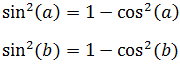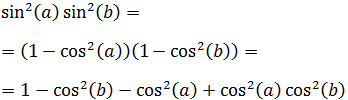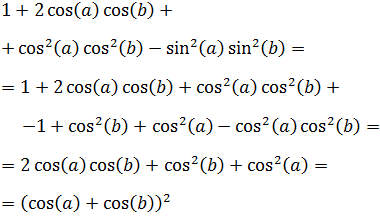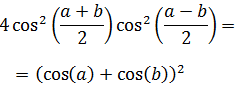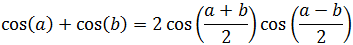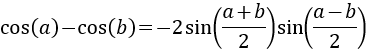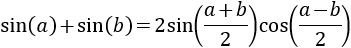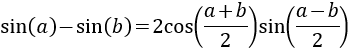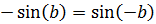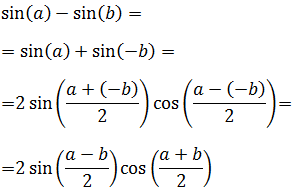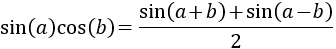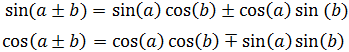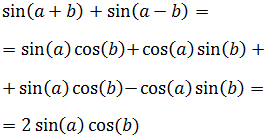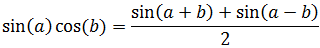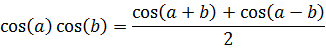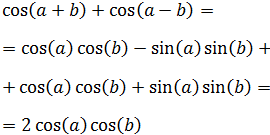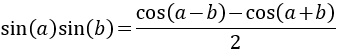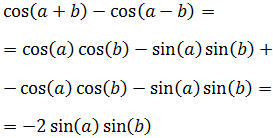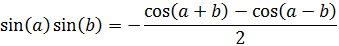Las identidades trigonómetricas son igualdades entre funciones trigonométricas que se utilizan con frecuencia. Un ejemplo de estas identidades es la identidad fundamental de la trigonometría:
$$ \cos^2(\alpha ) + \sin^2(\alpha ) = 1$$
A continuación demostramos las identidades trigonométricas más importantes: Identidad trigonométrica fundamental; Secante al cuadrado; Cosecante al cuadrado; Seno y coseno del ángulo opuesto; Seno y coseno de un ángulo más/menos π; Seno, coseno y tangente de la suma de ángulos; Seno, coseno y tangente del ángulo doble; Coseno del ángulo medio o ángulo mitad; Seno del ángulo medio o ángulo mitad; Tangente del ángulo medio o ángulo mitad; Suma de cosenos; Resta de cosenos; Suma de senos; Resta de senos; Producto de seno y coseno; Producto de cosenos y Producto de senos.
1. Identidad trigonométrica fundamental
$$ \sin^2 (a) + \cos^2 (a) = 1 $$
Demostración
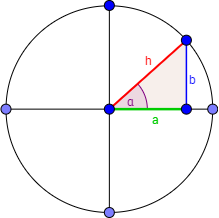
Usaremos las definiciones del seno y del coseno:
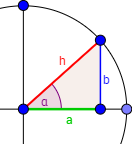
El seno es el cateto opuesto entre la hipotenusa y el coseno es el cateto contiguo entre la hipotenusa:
$$ \sin(\alpha) = \frac{b}{h} $$
$$ \cos(\alpha) = \frac{a}{h} $$
Sumamos los cuadrados del seno y del
coseno y aplicamos su definición:
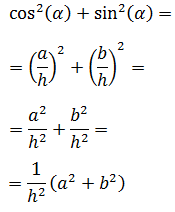
Observad que el triangulo de la imagen es rectángulo, por lo que
podemos aplicar el teorema de Pitágoras que nos dice que la suma de los cuadrados de los catetos es el cuadrado de la hipotenusa, esto es,
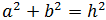
Por tanto,
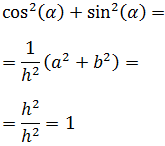
Ejemplos
-
Si \(\alpha = 3\pi /4 \text{ rad}\) (radianes),
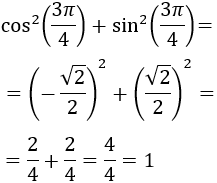
-
Si \(\alpha = 45^\circ \) (grados),
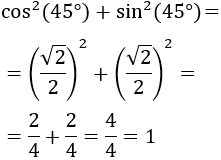
2. Secante al cuadrado
$$ \sec^2 (\alpha ) = 1+\text{tg}^2 (\alpha ) $$
Demostración
Recordamos las definiciones de la tangente y la secante:
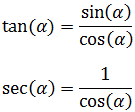
Vamos a desarrollar la parte derecha de la igualdad sustituyendo la tangente por su definición y aplicando la identidad trigonométrica fundamental en el paso =*:
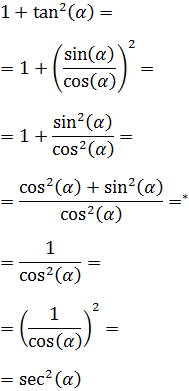
Ejemplo
Si \(\alpha = 135^\circ\). Por un lado tenemos,
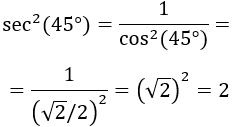
Por otro,
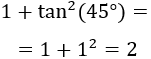
3. Cosecante al cuadrado
$$ \text{cosec}^2 (\alpha ) =1 + \text{cotg}^2 (\alpha ) $$
Demostración
Usaremos las definiciones de la cosecante, la tangente y la cotangente:
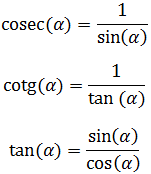
Desarrollamos el lado derecho escribiendo la definición de la tangente y aplicando la identidad trigonométrica fundamental:
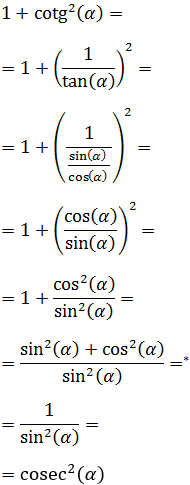
4. Ángulos opuestos
$$ \sin (-\alpha ) = - \sin(\alpha ) $$
$$ \cos (- \alpha ) = \cos (\alpha ) $$
Demostración
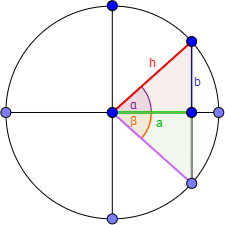
Observad que tenemos dos triángulos rectángulos iguales: los catetos e hipotenusas miden lo mismo y los ángulos tienen la misma amplitud (β = -α).
Si identificamos el coseno con el cateto contiguo al ángulo (el horizontal) y el seno con el cateto opuesto (el vertical), entonces observando la imagen anterior es fácil ver que
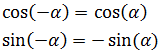
Nota: obsérvese que el seno es no negativo (o sea, positivo ó 0) en los cuadrantes I y II y no positivo (o sea, negativo ó 0) en los cuadrantes III y IV; mientras que el coseno es no negativo en los cuadrantes I y IV y no positivo en los cuadrantes II y III.
Ejemplo
Sea \( \alpha = 45^\circ\).
- El ángulo \(\alpha\) está en el cuadrante I, por lo que su coseno es positivo; el ángulo \(-\alpha\) se encuentra en el cuadrante IV, por lo que su coseno es también positivo:
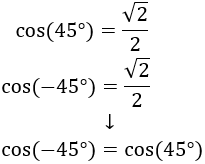
- El seno es no negativo en el cuadrante I y no positivo en el cuadrante IV:
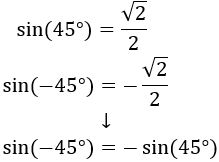
5. Ángulos más/menos π
$$ \sin ( \pi \pm \alpha ) = \mp \sin(\alpha ) $$
$$ \cos ( \pi \pm \alpha ) = - \cos(\alpha ) $$
Demostración
Caso π - α (cuadrantes I y II):
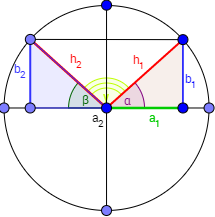
Los ángulos α y β tienen la misma amplitud (α = β). Obsérvese también que también coinciden las longitudes de los catetos b1 y b2 y la de los catetos a1 y a2.
Observando la imagen anterior es fácil ver que
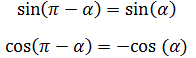
Caso π + α (cuadrantes I y III):
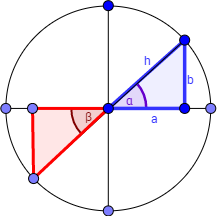
Observando la imagen anterior es fácil ver que
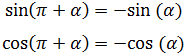
Podemos reescribir las cuatro identidades utilizando los signos más menos y menos más:
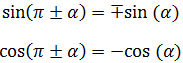
Ejemplos
-
Sea \(\alpha = \pi /4\text{ rad}\) (\(\alpha = 45^\circ \)), su seno es \(\sin (\alpha ) = \sqrt{2}/2\).
Sumamos y restamos \(\pi\):
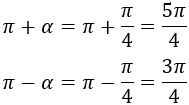
Seno de la suma:
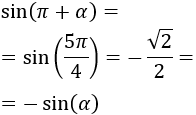
Seno de la resta:
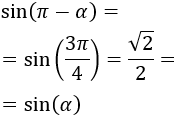
-
Sea ahora \(\alpha = 30^\circ\), su coseno es \(\cos (\alpha ) = \sqrt{3}/2\).
Como estamos trabajando con grados, en lugar de \(\pi\) debemos sumar/restar 180 grados.
Calculamos el coseno de la suma:
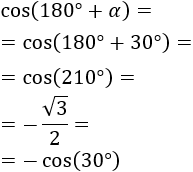
6.Suma de Ángulos
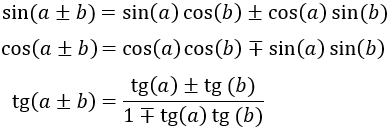
Demostramos estas fórmulas en la página seno, coseno y tangente de la suma y la resta de ángulos.
7. Ángulo Doble
$$ \sin(2a) = 2\sin(a)\cos(a) $$
$$ \cos(2a) = \cos^2(a) - \sin^2 (a) $$
$$ \text{tg}(2a) = \frac{2\text{tg}(a)}{1- \text{tg}^2(a)} $$
Demostración
Estas demostraciones son fáciles
teniendo en cuenta las identidades de la suma.
Sólo hay que considerar b = a en el seno y coseno de la suma:
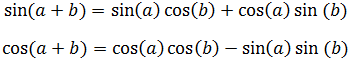
Veamos ahora el coseno, seno y tangente del ángulo mitad:
8. Coseno del Ángulo Medio o Ángulo Mitad
$$ \cos \left( \frac{\alpha }{2} \right) = \pm \sqrt{ \frac{1 + \cos(\alpha )}{2}} $$
Demostración
Aplicaremos la fórmula del coseno de la suma y la identidad trigonométrica fundamental, es decir,
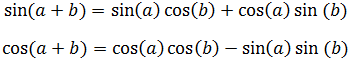
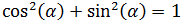
Podemos escribir \(\cos(\alpha )\) como el coseno de la suma de los ángulos \(\alpha /2\) y \(\alpha /2\):
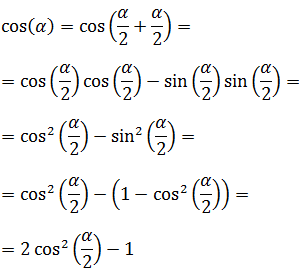
Nota: en la penúltima igualdad se ha sustituido el seno al cuadrado a partir de la identidad trigonométrica fundamental:
\( \sin^2(\alpha /2) = 1 - \cos^2(\alpha /2)\)
Es decir, tenemos la igualdad:
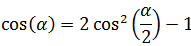
Aislamos la parte que nos interesa:
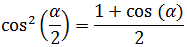
Finalmente, hacemos la raíz cuadrada:
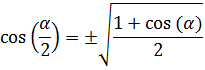
Nota: observad la importancia del signo ± al hacer la raíz cuadrada. El signo a escoger dependerá del ángulo en cuestión. Por ejemplo, si \(\alpha = 315^\circ\), habrá que escoger el signo negativo ya que el ángulo \(\alpha /2 = 157.5^\circ\) se encuentra en el cuadrante II y, por tanto, su coseno es negativo.
9. Seno del Ángulo Medio o Ángulo Mitad
$$ \sin \left( \frac{\alpha }{2} \right) = \pm \sqrt{ \frac{1 - \cos(\alpha )}{2}} $$
Demostración
En esta demostración vamos a utilizar una igualdad que hemos escrito en la demostración
anterior (obtenida de la tercera línea del desarrollo del coseno de α):
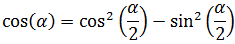
Despejamos el seno al cuadrado y sustituimos el coseno al cuadrado de α/2 por el radicando de la fórmula que hemos demostrado previamente:
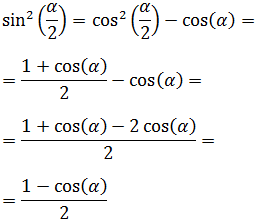
Finalmente, hacemos la raíz cuadrada a ambos lados de la igualdad:
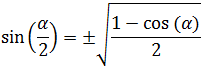
Nota: el signo de la fórmula dependerá del ángulo, como ya hemos comentado en la demotración anterior.
10. Tangente del Ángulo Medio o Ángulo Mitad
$$ \text{tg} \left( \frac{\alpha }{2} \right) = \pm \sqrt{ \frac{1 - \cos(\alpha )}{1 + \cos(\alpha )}} $$
Demostración
Esta demostración es muy sencilla ya que sólo tenemos que aplicar las fórmulas del seno y del
coseno del ángulo medio a la definición de la tangente, que es el cociente del seno y coseno:
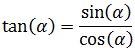
Calculamos la tangente del ángulo medio:
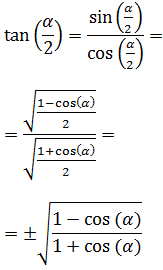
Veamos ahora sumas y restas de funciones trigonométricas:
11. Suma de Cosenos
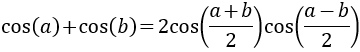
Demostración
Elevamos al cuadrado el lado derecho de la igualdad y operamos aplicando las fórmulas del ángulo medio y del coseno de la suma y de la resta:
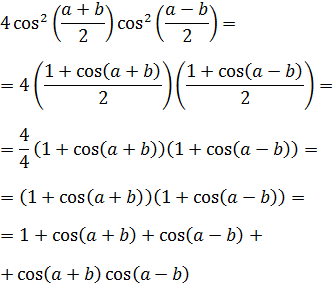
Llamamos a la suma anterior Suma (*).
Podemos reescribir los sumandos segundo y tercero de Suma (*) aplicando las fórmulas del coseno de la suma y de la resta:
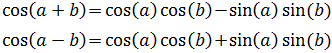
Al sumarlos tenemos:
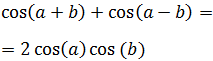
Y al multiplicarlos:
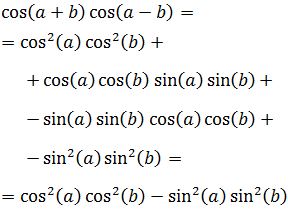
Por tanto, la suma Suma (*) es
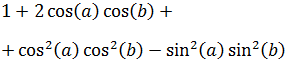
Recordad que podemos escribir
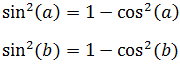
Con lo que el último sumando de Suma (*) es
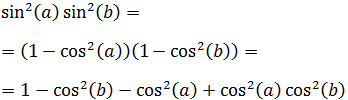
De este modo tenemos que Suma (*) es
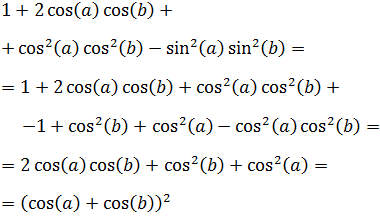
Nota: en el último paso hemos aplicado la fórmula del cuadrado de la suma en sentido contrario: \( (a+b)^2 = a^2 + b^2 + ab\).
Luego tenemos
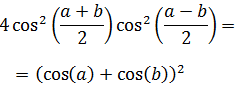
Finalmente, hacemos la raíz cuadrada y obtenemos la identidad buscada:
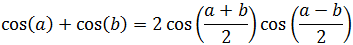
12. Resta de Cosenos
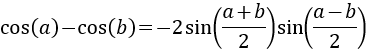
No demostramos esta identidad puesto que es similar a la resta de senos (demostrada más adelante).
13. Suma de Senos
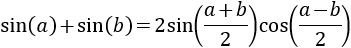
No demostramos esta identidad puesto que es similar a la suma de cosenos (demostrada anteriormente).
14. Resta de Senos
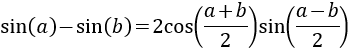
Demostración
Teniendo en cuenta que el seno del ángulo opuesto es
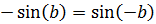
Entonces, aplicando la suma de los senos, tenemos
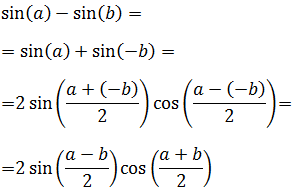
Veamos ahora productos de funciones trigonométricas escritos como sumas y restas:
15. Producto de seno y coseno
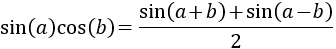
Demostración
Recordamos que el coseno y el seno de la suma y de la resta son
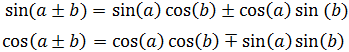
La suma de los senos de la suma y de la resta es:
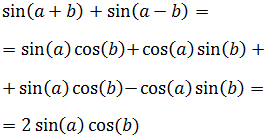
Por tanto,
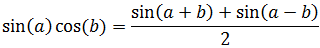
16. Producto de cosenos
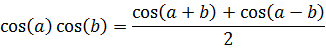
Demostración
Procedemos del mismo modo que en la demostración anterior pero con cosenos:
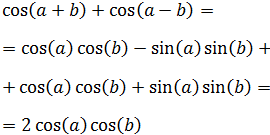
Por tanto,
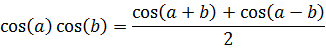
17. Producto de senos
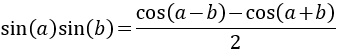
Demostración
El procedimiento es análogo a los anteriores:
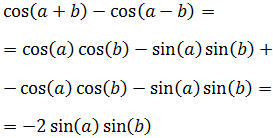
Por tanto,


Identidades trigonométricas -
© -
matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.