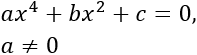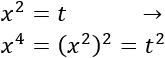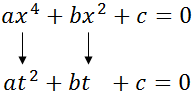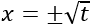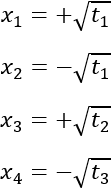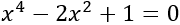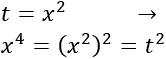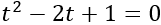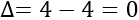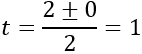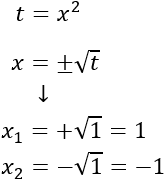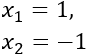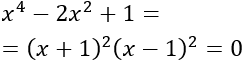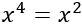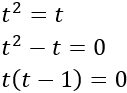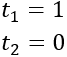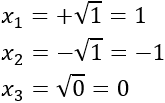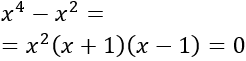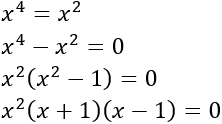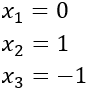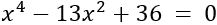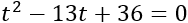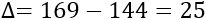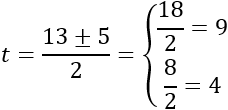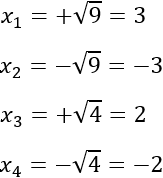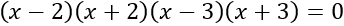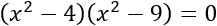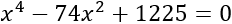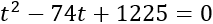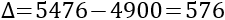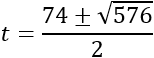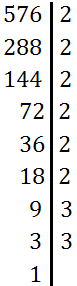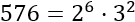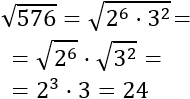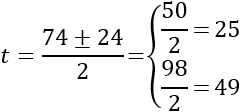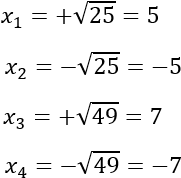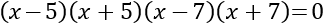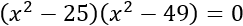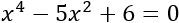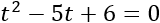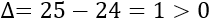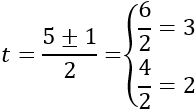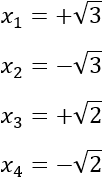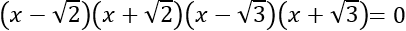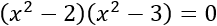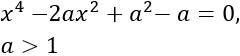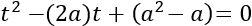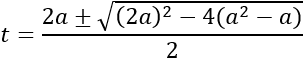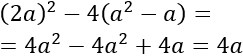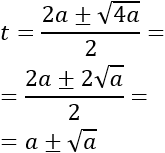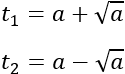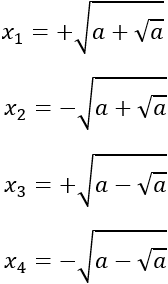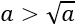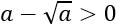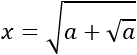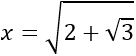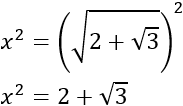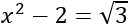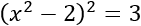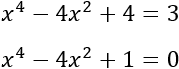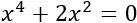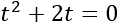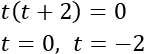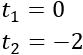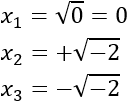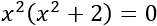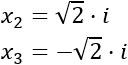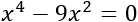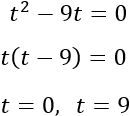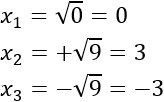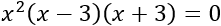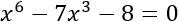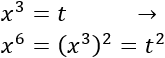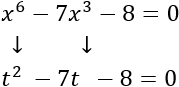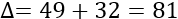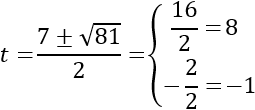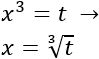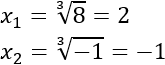Problema 1
Resolver y factorizar la siguiente ecuación bicuadrada:
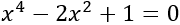
Ver solución
Aplicamos el cambio de variable siguiente:
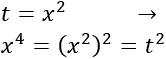
La ecuación se transforma en la ecuación de segundo grado:
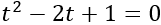
El discriminante de la ecuación anterior es
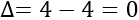
Por tanto, la ecuación de segundo grado sólo tiene una solución y es
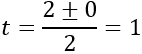
Ahora, deshacemos el cambio de variable:
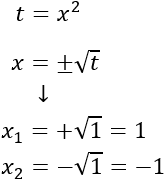
La ecuación bicuadrada tiene dos soluciones distintas:
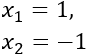
Factorizamos la ecuación:
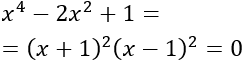
Problema 2
Resolver y factorizar la siguiente ecuación bicuadrada:
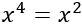
Ver solución
Esta ecuación la vamos a resolver de dos formas.
Primera forma:
Si aplicamos el método de cambio de variable anterior (\(t=x^2\)), obtenemos
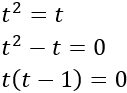
Por tanto, las soluciones de la ecuación de segundo grado son
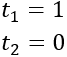
Deshacemos el cambio de variable:
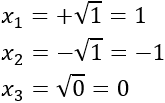
Observad que solo hay 3 soluciones distintas porque el 0 no tiene signo.
Factorizamos la ecuación:
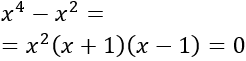
Segunda forma:
La segunda forma es escribir la ecuación de forma factorizada, sin aplicar el cambio de variable habitual:
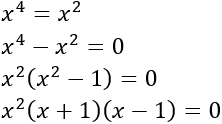
En el último paso hemos aplicado el producto notable: suma por diferencia igual a diferencia de cuadrados.
Como la ecuación está factorizada, podemos deducir directamente las tres soluciones distintas de la ecuación bicuadrada:
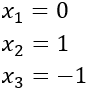
Problema 3
Resolver y factorizar la siguiente ecuación bicuadrada:
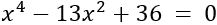
Ver solución
Aplicamos el cambio de variable \(t=x^2\) y obtenemos la ecuación de segundo grado
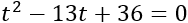
Su discriminante es
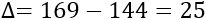
Por tanto, las soluciones son
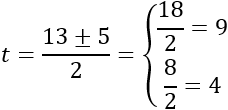
Calculamos las soluciones de la ecuación de cuarto grado:
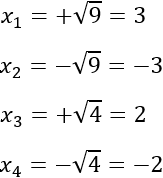
Tenemos cuatro soluciones distintas.
La factorización de la ecuación es:
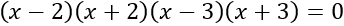
O también,
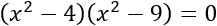
Problema 4
Resolver y factorizar la siguiente ecuación bicuadrada:
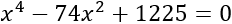
Ver solución
Aplicamos el cambio de variable \(t=x^2\) y obtenemos la ecuación de segundo grado siguiente:
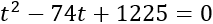
Su discriminante es
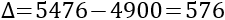
Y, por tanto, sus soluciones son
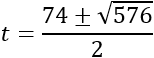
Para calcular la raíz cuadrada de 576 manualmente, descomponemos dicho número:
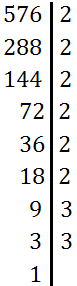
Por tanto, la descomposición de 576 es
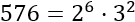
Calculamos su raíz cuadrada:
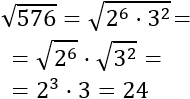
Luego las soluciones son
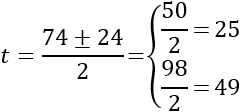
Y, finalmente, calculamos las soluciones de la ecuación bicuadrada:
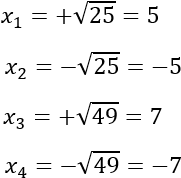
Hay cuatro soluciones reales distintas.
Factorizamos la ecuación:
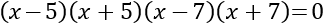
O bien,
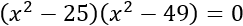
Problema 5
Resolver y factorizar la siguiente ecuación bicuadrada:
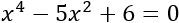
Ver solución
Aplicamos el cambio de variable \(t=x^2\) y obtenemos la ecuación cuadrática
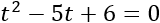
Cuyo discriminante es
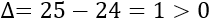
Las soluciones de la ecuación cuadrática son
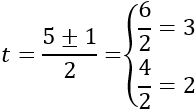
Por tanto, las cuatro soluciones (distintas) de la ecuación bicuadrada son
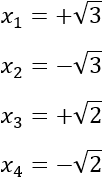
La ecuación factorizada es:
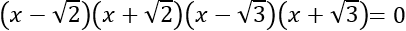
O bien,
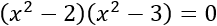
Problema 6 (dificultad alta)
Considerar la siguiente ecuación de cuarto grado donde \(a\) es un parámetro:
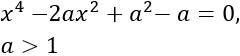
Cuestiones:
Ver solución
Es una ecuación bicuadrada.
Procedemos de igual modo que en los problemas anteriores. La única diferencia es que tenemos el parámetro \(a\), por lo que no podremos simplificar mucho las soluciones.
Aplicamos el cambio de variable \(t=x^2\) y obtenemos la ecuación de segundo grado siguiente:
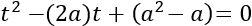
Utilizamos los paréntesis para enfatizar los 3 coeficientes de la ecuación de segundo grado.
Aplicamos la fórmula para obtener las soluciones:
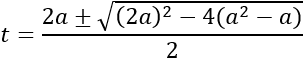
Simplificamos el radicando:
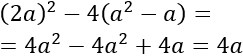
Por tanto,
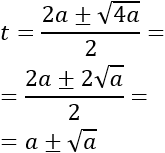
Luego tenemos dos soluciones:
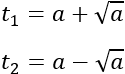
Deshacemos el cambio de variable y obtenemos las 4 soluciones de la ecuación bicuadrada:
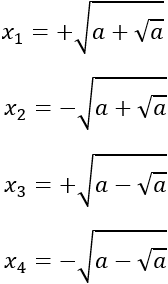
Exigimos que \(a > 1\) porque sólo en este caso se cumple que
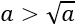
Y, por tanto,
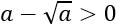
De este modo, aseguramos que los radicandos de las dos últimas soluciones sean positivos y, por tanto, cada una de ellas es una solución real.
Un caso especial es cuando \(a=0\). Entonces, la ecuación de cuarto grado sólo tiene una solución: \(x=0\).
Problema 7
La ecuación del problema anterior ha sido obtenida buscando una ecuación que tuviera al menos la solución
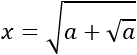
Encontrar una ecuación bicuadrada que tenga al menos la solución
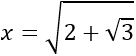
Ver solución
Lo que haremos es usar la igualdad del enunciado:
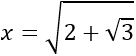
Esta igualdad se puede ver como una ecuación de primer grado.
Vamos a elevar al cuadrado dos veces. Así, tendremos una ecuación de cuarto grado:
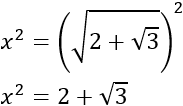
Antes de volver a elevar al cuadrado, pasamos el 2 a la izquierda para que la raíz cuadrada quede aislada:
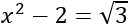
Elevamos al cuadrado:
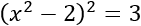
Desarrollamos el cuadrado de la resta:
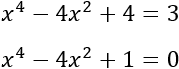
Problema 8
Resolver y factorizar la siguiente ecuación bicuadrada:
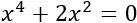
Ver solución
Aplicamos el cambio de variable \(t=x^2\) y obtenemos
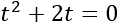
Resolvemos la ecuación de segundo grado incompleta:
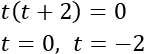
Tenemos las soluciones
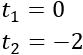
Deshacemos el cambio de variable:
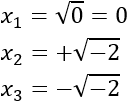
Como no existen las raíces de negativos, la ecuación bicuadrada sólo tiene una solución (real): \(x = 0\).
Una factorización de la ecuación es:
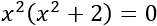
Soluciones complejas:
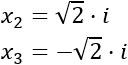
Problema 9
Resolver y factorizar la siguiente ecuación bicuadrada:
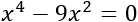
Ver solución
Aplicamos el cambio de variable de siempre y resolvemos la ecuación de segundo grado incompleta que obtenemos:
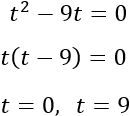
Deshacemos el cambio de variable:
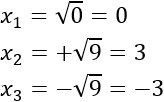
Por tanto, la ecuación bicuadrada tiene 3 soluciones distintas.
Una factorización de la ecuación es
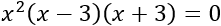
Problema 10 (dificultad alta)
El método del cambio de variable o sustitución lo podemos aplicar en otros casos. Por ejemplo, para algunas ecuaciones de sexto grado.
Aplicad el cambio de variable para calcular las soluciones (reales) de la siguiente ecuación:
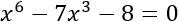
Ver solución
Aplicamos el cambio de variable \(t = x^3\):
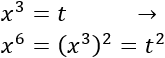
Obtenemos una ecuación de segundo grado:
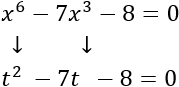
El discriminante de la ecuación es
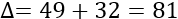
Por tanto, sus soluciones son
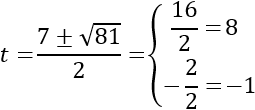
Deshacemos el cambio de variable:
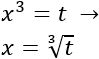
Calculamos las soluciones:
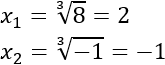
Por tanto, la ecuación de sexto grado tiene dos soluciones reales distintas.
No escribimos las soluciones complejas ya que son un poco complicadas de obtener (porque son raíces cúbicas).


Ecuaciones bicuadradas resueltas -
© matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.