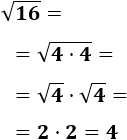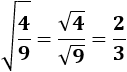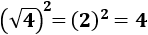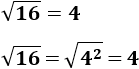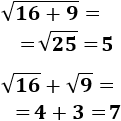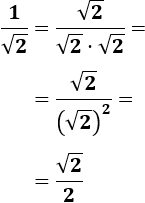Raíces cuadradas (test)
Nivel 2: propiedades de las raíces cuadradas
Contenido de esta página:
- Recordatorio de las propiedades.
- Test online de las propiedades de las raíces cuadradas.
Este test es sobre las propiedades de las raíces cuadradas, las cuales vamos a recordar ahora. El concepto de raíz cuadrada (positiva y negativa) lo vimos en el test anterior (concepto de raíz cuadrada).
Nota: no vamos a calcular raíces de números negativos.
Siguiente test sobre raíces: raíces n-ésimas.
Otras páginas:
Antes del test, vamos a hacer un breve recordatorio a modo de introducción.
1. Propiedades de las raíces cuadradas
Raíz de un producto:
La raíz cuadrada de un producto de factores es el producto de las raíces de los factores:
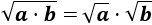
Raíz de un cociente:
La raíz cuadrada de un cociente de factores es el cociente de las raíces de los factores:
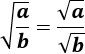
Raíz cuadrada al cuadrado:
Al elevar al cuadrado una raíz cuadrada, el signo radical desaparece:
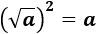
Esto se debe a que la raíz cuadrada es la operación inversa de la potenciación al cuadrado:
La raíz cuadrada de \(a\) es el número cuyo cuadrado es \(a\). Por tanto, al elevar al cuadrado el número cuyo cuadrado es \(a\), obtenemos \(a\)."
Raíz cuadrada de un cuadrado:
La raíz cuadrada de un número al cuadrado es el propio número (la base de la potencia):
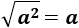
Raíz cuadrada de una suma:
La raíz cuadrada de dos números no negativos es menor o igual que la suma de las raíces de dichos números:
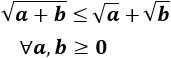
En realidad, la igualdad sólo se da cuando \(a=0\) ó \(b=0\).
Racionalizar:
Se denomina racionalizar al proceso por el cual se sustituye una expresión matemática con raíces en el denominador por otra equivalente sin raíces en el denominador.