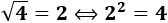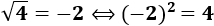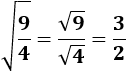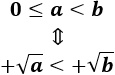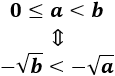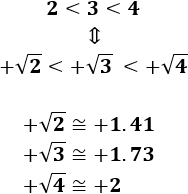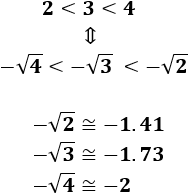Raíces cuadradas (test)
Nivel 1: concepto de raíz cuadrada
Contenido de esta página:
- Recordatorio
- Test online de raíces cuadradas.
En este test vamos a repasar el concepto de raíz cuadrada. No vamos a entrar en las propiedades de las raíces todavía, pero si veremos algunas propiedades básicas.
Nota: no vamos a calcular raíces de números negativos. De hecho, vamos a considerar que éstas no existen.
Siguientes test sobre raíces:
- Test nivel 2: propiedades de las raíces cuadradas
- Test nivel 3: raíces n-ésimas
Otras páginas:
Antes del test, vamos a hacer un breve recordatorio a modo de introducción.
1. Concepto de raíz cuadrada
Recordad que...
La raíz cuadrada de un número (positivo) \(a\) se representa por \(\sqrt{a}\) y es el número o los números \(b\) cuyo cuadrado es \(a\).
Es decir, la raíz cuadrada de \(a\) es \(b\) si \(b\) al cuadrado es \(a\).
Dicho matemáticamente,
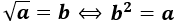
Nombres: en la expresión \(\sqrt{a} = b\),
- El número \(a\) se llama radicando.
- El símbolo \(\sqrt{\ }\) se llama signo radical.
- El número \(b\) se llama raíz cuadrada de \(a\).
Como se observa en los ejemplos,
Todo número positivo tiene dos raíces cuadradas. La diferencia entre ellas es sólo el signo.
Para indicar que la raíz cuadrada son dos números que sólo se diferencian en el signo, utilizaremos el signo \(\pm\). Por ejemplo, escribimos \(\sqrt{4} = \pm 2\) para decir que tanto \(-2\) como \(+2\) son raíces cuadradas de \(4.\)
Otra opción es no escribir ningún signo. Por ejemplo, \(\sqrt{4} = 2\).
Finalmente, tenemos que decir que para nosotros (nivel de secundaria), no existen las raíces cuadradas de números negativos:
El radicando de una raíz cuadrada siempre debe ser \(a ≥ 0\)
Esto se debe a que el cuadrado de un número (real) no puede ser negativo y, por tanto, no hay raíces de números negativos.