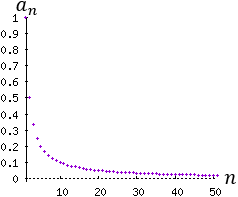
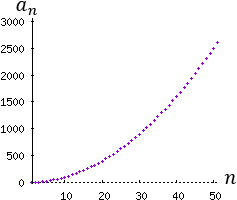
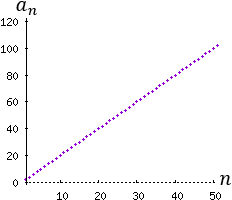
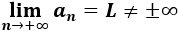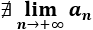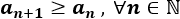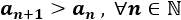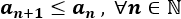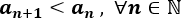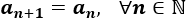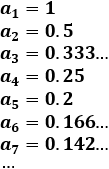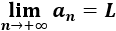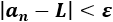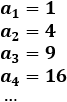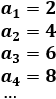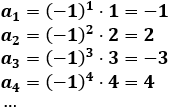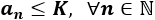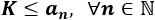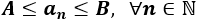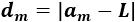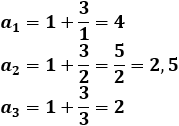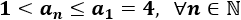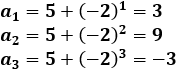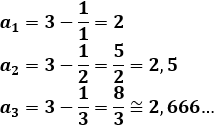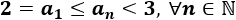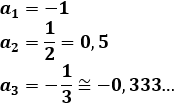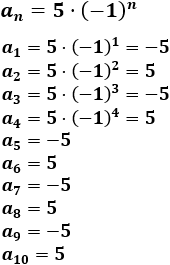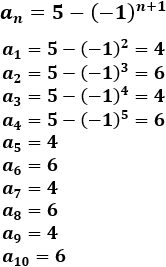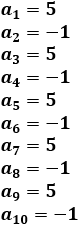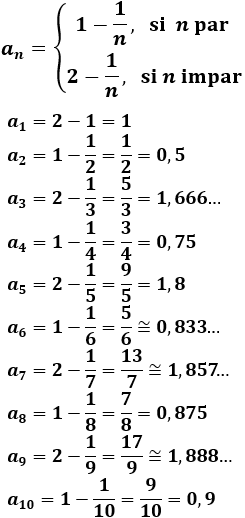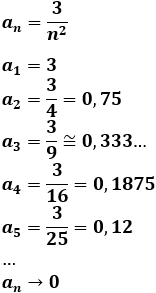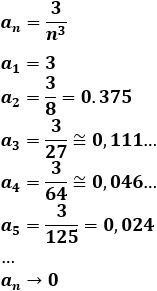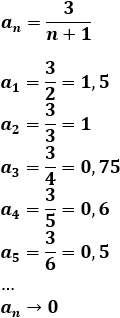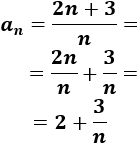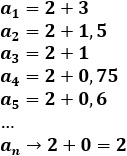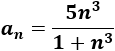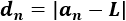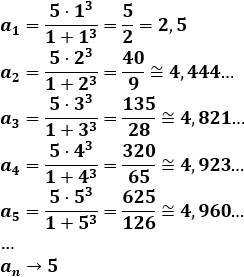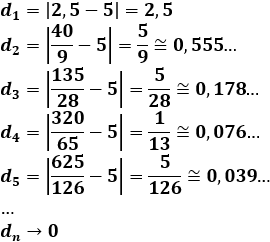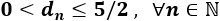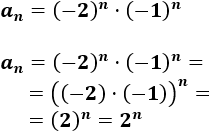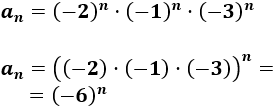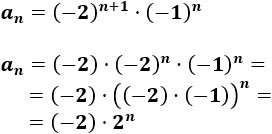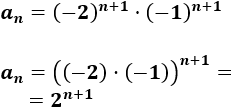Problema 1
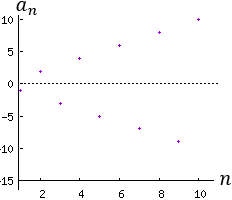
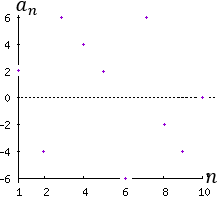
Determinar si las siguientes sucesiones son crecientes, decrecientes o constantes:
Ver solución
La primera y la quinta son crecientes.
La segunda y la cuarta son decrecientes.
La tercera es constante.
La sexta sucesión no es contante, ni creciente ni decreciente (es oscilante). Por tanto, la respuesta a la pregunta es que no.
Problema 2
Calcular los términos \(a_1\), \(a_2\) y \(a_3\) de las siguientes sucesiones y determinar
-
si son crecientes, decrecientes o constantes,
-
si convergen o divergen,
-
si son alternadas u oscilantes y
-
si son acotadas.
Sucesión 1:
Sucesión 2:
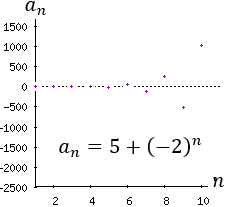
Sucesión 3:

Sucesión 4:
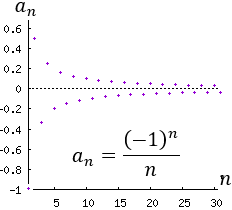
Ver solución
Sucesión 1:
Calculamos los 3 primeros términos:
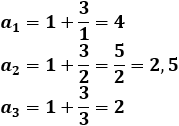
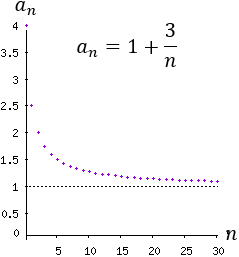
Es una sucesión decreciente y convergente a 1. No es alternada ni oscilante.
Está acotada superiormente por el primer término e inferiormente por el límite:
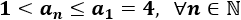
Sucesión 2:
Calculamos los 3 primeros términos:
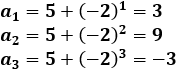
No es ni creciente ni decreciente porque es alternada (por tanto, no oscilante). No es convergente ni acotada.
Sucesión 3:
Calculamos los 3 primeros términos:
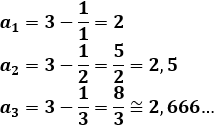
Es una sucesión creciente y convergente a 3. No es alternada ni oscilante.
Está acotada inferiormente por el primer término y superiormente por el límite:
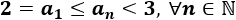
Sucesión 4:
Calculamos los 3 primeros términos:
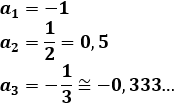
No es ni creciente ni decreciente porque es alternada. No es oscilante. Es convergente a 0.
Está acotada superiormente por el segundo término e inferiormente por el primero:

Problema 3
Calcular los 10 primeros términos de las siguientes sucesiones y determinar si son alternadas u oscilantes:
-
\(a_n = 5·(-1)^n\)
-
\(a_n = 5-(-1)^{n+1}\)
-
\( a_n =
\begin{cases}
-1, & \quad \text{si } n \text{ es par}\\
5, & \quad \text{si } n \text{ es impar}
\end{cases} \)
-
\( a_n =
\begin{cases}
1-\frac{1}{n}, & \quad \text{si } n \text{ es par}\\
2-\frac{1}{n}, & \quad \text{si } n \text{ es impar}
\end{cases} \)
Ver solución
-
\(a_n = (5·(-1))^n\)
Calculamos los 10 primeros términos:
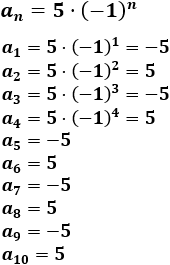
La sucesión es alternada.
-
\(a_n = 5-(-1)^{n+1}\)
Calculamos los 10 primeros términos:
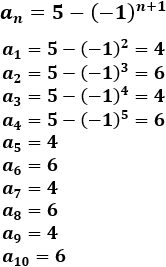
La sucesión es oscilante.
-
\( a_n =
\begin{cases}
-1, & \quad \text{si } n \text{ es par}\\
5, & \quad \text{si } n \text{ es impar}
\end{cases} \)
Calculamos los 10 primeros términos:
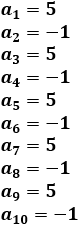
La sucesión es alternada.
-
\( a_n =
\begin{cases}
1-\frac{1}{n}, & \quad \text{si } n \text{ es par}\\
2-\frac{1}{n}, & \quad \text{si } n \text{ es impar}
\end{cases} \)
Calculamos los 10 primeros términos:
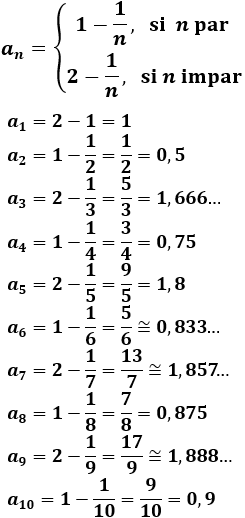
La sucesión es oscilante.
Problema 4
¿Una sucesión constante puede ser divergente?
Ver solución
No, las sucesiones constantes siempre son convergentes.
Por ejemplo, la sucesión constante \(a_n=2\) converge a 2:
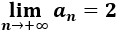
Problema 5
Una sucesión convergente se aproxima a su límite, ¿puede alcanzarlo?
Ver solución
Depende de la sucesión. Algunas sucesiones convergentes no alcanzan su límite, como la sucesión \(a_n=1/n\) que converge a 0, pero ninguno de sus términos es 0. Las sucesiones constantes son convergentes y todos sus términos son iguales al límite.
Problema 6
Calcular el límite de las siguientes sucesiones:
Ver solución
Vamos a calcular los 5 primeros términos para ver la evolución de las sucesiones.
-
\( a_n = \frac{3}{n^2} \)
Los 5 primeros términos son
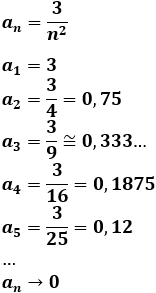
Al dividir entre el cuadrado de la posición, cada vez se obtienen números más pequeños y próximos a 0.
El límite de la sucesión es 0.
-
\( a_n = \frac{3}{n^3}\)
Los 5 primeros términos son
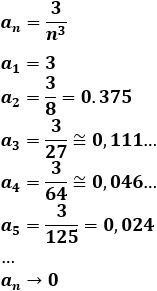
Al dividir entre el cubo de \(n\), los términos son cada vez más pequeños y se aproximan a 0.
El límite es 0.
-
\( a_n = \frac{3}{n+1}\)
Los 5 primeros términos son
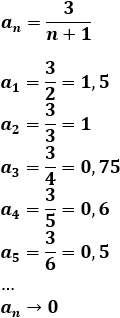
Al igual que en las sucesiones anteriores, el denominador aumenta en cada término mientras que el numerador es constante. Los términos son cada vez más pequeños y próximos a 0.
El límite es 0.
-
\( a_n = \frac{2n+3}{n}\)
Operamos un poco en el término general:
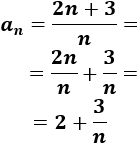
Todos los términos son mayores que 2 porque tenemos la suma de 2 y una fracción positiva. La fracción cada vez es más pequeña y se aproxima a 0, así que la sucesión va decreciendo y aproximándose a 2:
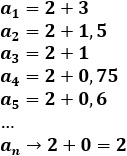
Problema 7
Sea la sucesión
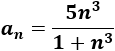
Calcular los 5 primeros términos para deducir cuál es su límite \(L\) y calcular la distancia entre dichos términos y \(L\).
Nota: la distancia entre el término \(a_n\) y el límite \(L\) es
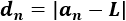
¿Qué tipo de sucesión es \(d_n\)?
Ver solución
Calculamos los 5 términos:
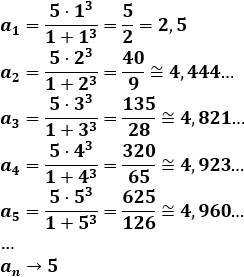
Deducimos que el límite de la sucesión es \(L=5\).
Calculamos la distancia entre los primeros términos y el límite:
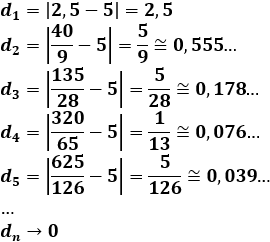
La sucesión \(d_n\) es decreciente y convergente a 0 (porque la distancia entre los términos \(a_n\) y su límite es cada vez más pequeña). Además, \(d_n\) está acotada superior e inferiormente:
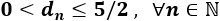
Problema 8
Determinar si las siguientes sucesiones son alternadas sin calcular sus términos:
-
\(a_n = (-2)^n·(-1)^n\)
-
\(a_n = (-2)^n·(-1)^n·(-3)^n\)
-
\(a_n = (-2)^{n+1}·(-1)^n\)
-
\(a_n = (-2)^{n+1}·(-1)^{n+1}\)
Ver solución
Tenemos que tener en cuenta que la potencia de un número negativo es positiva si el exponente es par y es negativa si el exponente es impar.
-
Operamos un poco:
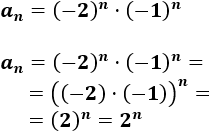
La sucesión es siempre positiva por ser la potencia de un número positivo.
No es alternada.
-
Operamos un poco:
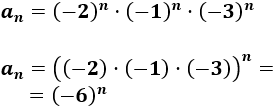
La sucesión es alternada por ser las potencias de un número negativo.
-
Operamos un poco:
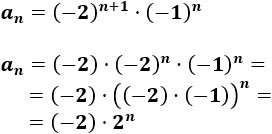
La sucesión siempre es negativa: es el producto de un negativo por una potencia que siempre es positiva.
No es alternada.
-
Operamos un poco:
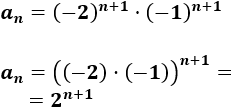
La sucesión es siempre positiva.
No es alternada.
Problema 9
¿Una sucesión alternada puede tener límite?
Ver solución
Sí. Por ejemplo, la siguiente sucesión es alternada y su límite es 0:
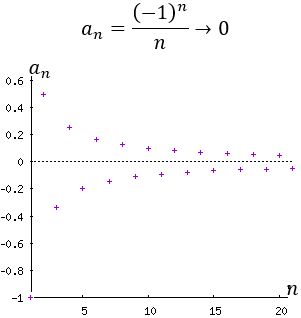
Problema 10
Determinar si la sucesión de las potencias de 2 (es decir, \(a_n=2^n\)) es
-
creciente, decreciente o alternada;
-
convergente o divergente;
-
oscilante o no oscilante;
-
acotada o no acotada.
Ver solución
Los primeros términos de la sucesión son 2, 4, 8, 16, 32, 64, 128,...
La sucesión es creciente, divergente, no oscilante y acotada inferiormente por 2 pero no acotada superiormente.