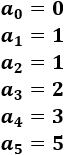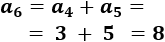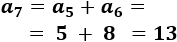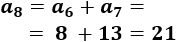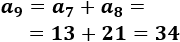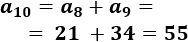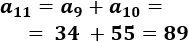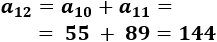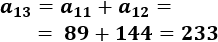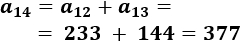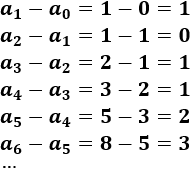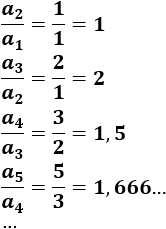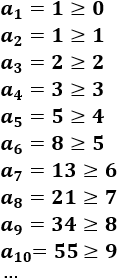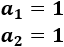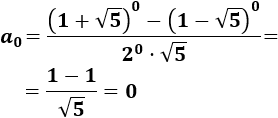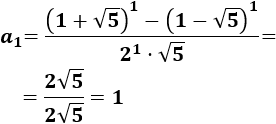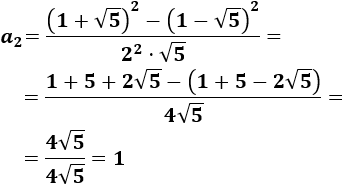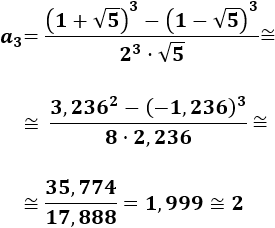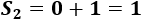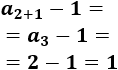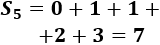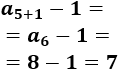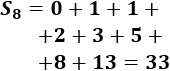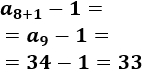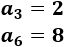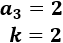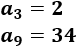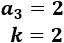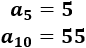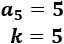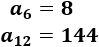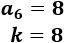Sucesión de Fibonacci
Contenido de esta página:
- Sucesión de Fibonacci
- Término general por recurrencia
- Monotonía y divergencia
- Número áureo
- Fórmula de Binet
- Propiedades de la sucesión
En esta página hablaremos de la famosa sucesión de Fibonacci. El texto es muy básico y accesible para los alumnos de Educación Secundaria. A lo largo del texto resolveremos 10 problemas sobre la sucesión.
Temas relacionados:
1. Sucesión de Fibonacci
\(0\), \(1\), \(1\), \(2\), \(3\), \(5\), \(8\), \(13\), \(21\), \(34\), ...
La sucesión de Fibonacci es conocida desde hace miles de años, pero fue Fibonacci (Leonardo de Pisa) quien la dio a conocer al utilizarla para resolver un problema.
El primer y segundo término de la sucesión son
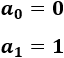
Los siguientes términos se obtienen sumando los dos términos que les preceden:
El tercer término de la sucesión es
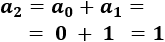
El cuarto término es
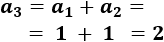
El quinto término es
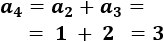
El sexto término es
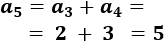
El \((n+1)\)-ésimo término es
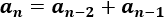
2. Término general
La sucesión de Fibonacci es una sucesión definida por recurrencia. Esto significa que para calcular un término de la sucesión se necesitan los términos que le preceden.
Se proporcionan los dos primeros términos: \(a_0=0\) y \(a_1=1\). Los siguientes se calculan con la siguiente fórmula:
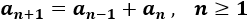
Nota: el primer término que proporciona la fórmula es \(a_2\) (porque \(n\) tiene que ser mayor o igual que 1). Por esta razón, se definen \(a_0\) y \(a_1\) con anterioridad.
Problema 1
Calcular los 15 primeros términos de la sucesión de Fibonacci.
Problema 2
¿Es una sucesión aritmética? ¿Y geométrica? ¿Por qué?
Problema 3
¿Es una sucesión creciente, decreciente o alternada? ¿Por qué?
Problema 4
¿La suma todos los términos de la sucesión es un número finito como en algunas progresiones geométricas?
3. Monotonía y divergencia
La sucesión de Fibonacci es creciente, es decir, cada término es mayor o igual que el que le precede:
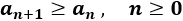
Nota: a partir de \(n=2\) la desigualdad es estricta, es decir, \(a_{n+1}> a_n\) para \(n≥ 2\).
La sucesión es creciente y no está acotada (superiormente). Esto implica que la sucesión es divergente (no convergente), es decir, no tiene límite. Por tanto, la sucesión crece indefinidamente.
Nota: puede servir como demostración el razonamiento del Problema 4.
Problema 5
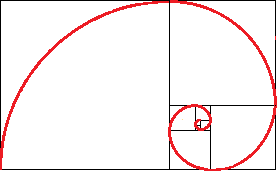
Espiral de Fibonacci:

La espiral de Fibonacci se traza uniendo dos vértices de cuadrados adosados. La longitud del lado de los cuadrados viene dada por la sucesión de Fibonacci.
¿Cuánto miden los lados de los 9 cuadrados de la figura?
Problema 6
El triángulo de Pascal:
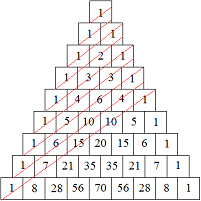
Para construir el triángulo de Pascal se escriben 1's en los dos lados del triángulo y se completa cada hueco sumando los dos números que tiene encima.
En la figura se han trazado en rojo las diagonales de un triángulo de Pascal con 9 filas. ¿Cuánto suman los números de cada diagonal?
Las sumas de los números de las diagonales son 1, 1, 2, 3, 5, 8, 13, 21 y 34. Se trata de la sucesión de Fibonacci.
4. Número áureo
El número áureo es el número irracional
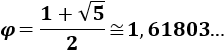
Su relación con la sucesión de Fibonacci es que es el límite de los cocientes de sus términos:
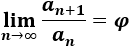
Esto significa que los cocientes de los términos consecutivos de la sucesión de Fibonacci se aproximan al número áureo.
Problema 7
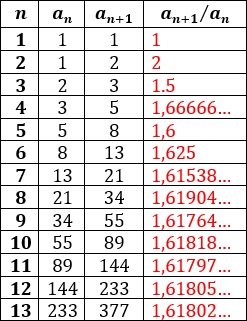
Completar la siguiente tabla con los cocientes de la sucesión de Fibonacci:
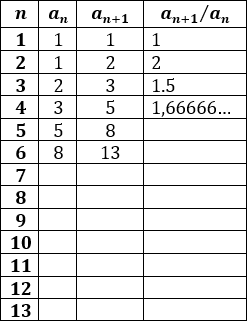
Observad que el límite de \(a_{n+1}/a_n\) es el número áureo φ ≅ 1,68033…
5. Fórmula de Binet
Aunque la sucesión se define por recurrencia, existe una fórmula para calcular un término de la sucesión sin necesidad de calcular los anteriores:
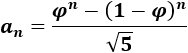
Operando un poco,
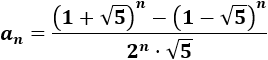
Sin embargo, este término general presenta el inconveniente de tener potencias de binomios y raíces.
Problema 8
Calcular los cuatro primeros términos de Fibonacci utilizando la fórmula de Binet.
6. Algunas propiedades
Entre las numerosas propiedades de la sucesión, destacamos estas tres por su sencillez:
-
Cada término es el promedio del término que ocupa dos posiciones anteriores y el que ocupa la siguiente:
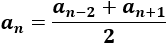
-
La suma de los \(n\) primeros términos, \(S_n\), es igual al término \(a_{n+1}\) menos 1:
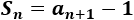
Tened en cuenta que la sucesión comienza con \(a_0\). Así, las primeras sumas son:
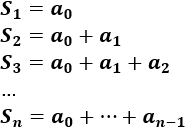
Por tanto, la suma hasta el término \(a_n\) es el término \(a_{n+2}\) menos 1.
-
El máximo común divisor de los números de Fibonacci que ocupan las posiciones \(n\) y \(m\) coincide con el término cuya posición es el máximo común divisor de \(n\) y \(m\):
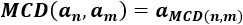
Problema 9
Calcular las sumas \(S_2\), \(S_5\) y \(S_8\) para comprobar la propiedad
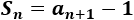
Problema 10
Comprobar la última propiedad dada (la del MCD) para las siguientes posiciones:
-
\(n=3\), \(m=6\)
-
\(n=3\), \(m=9\)
-
\(n=5\), \(m=10\)
-
\(n=6,\), \(m=12\)
Sucesión de Fibonacci - (c) - matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.