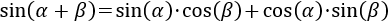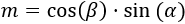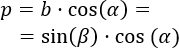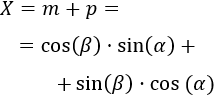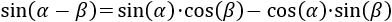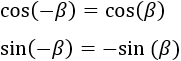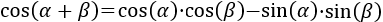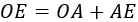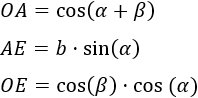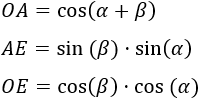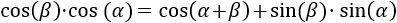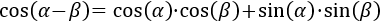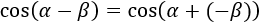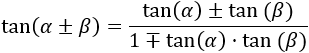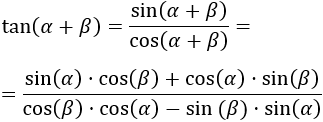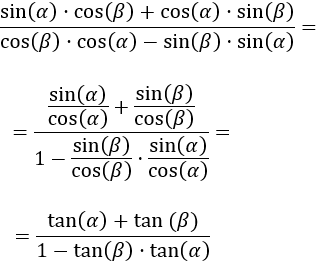Seno, coseno y tangente de la suma y la resta de ángulos

En esta página vamos a demostrar las fórmulas del seno, coseno y tangente de la suma y de la resta de ángulos:

Páginas relacionadas:

• Problemas de trigonometría básica
• Teorema del seno y teorema del coseno
• Demostraciones de las identidades trigonométricas básicas
• Más demostraciones de igualdades trigonométricas

A lo largo de todo el texto, consideramos sin pérdida de generalidad que el radio de la circunferencia es \(R=1\).

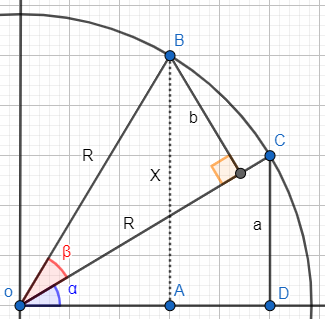
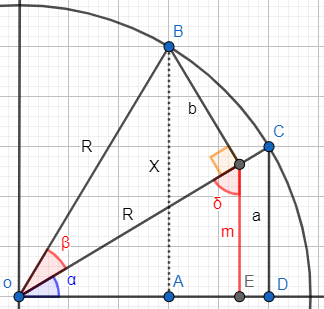
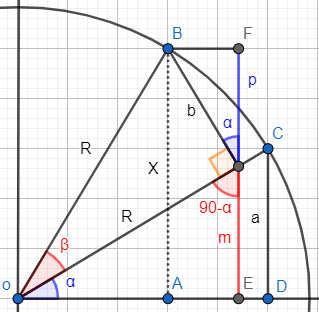
Consideremos la siguiente representación:

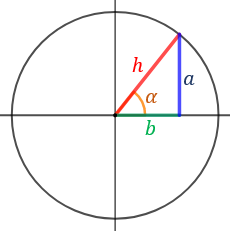
El radio de la circunferencia coincide con la hipotenusa del triángulo: \(R = h\).

El seno, coseno y tangente del ángulo \(\alpha\) se definen como

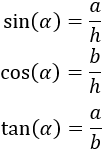
Por tanto, los lados \(a\) y \(b\) miden

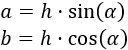
Es decir, los lados son el coseno o el seno multiplicados por la hipotenusa del triángulo con ángulo \(\alpha\).

En las demostraciones utilizaremos estas igualdades con triángulos cuyas hipotenusas no medirán lo mismo.

Nos apoyaremos en la siguiente representación:

Como el radio de la circunferencia es \(R=1\), entonces

• El segmento \(a\) es el seno ángulo \(\alpha\).

• El segmento \(b\) es el seno del ángulo \(\beta\).

• El segmento \(X\) (segmento discontinuo) es el seno del ángulo \(\alpha + \beta\).

Ahora vamos a calcular el segmento \(X\), es decir, el seno de la suma de los ángulos: \(sin(\alpha + \beta )\).

Trazamos el segmento \(m\) paralelo al segmento \(a\):

El ángulo \( \delta\) que aparece mide \( \delta = 90^\circ -\alpha\). Esto se debe a que los dos otros ángulos del triángulo miden \(\alpha\) y \(90^\circ\) y la suma de los tres ángulos debe ser \(180^\circ \):

$$ \delta = 180^\circ - \alpha - 90^\circ $$

$$ \delta = 90^\circ -\alpha $$

Teniendo en cuenta la introducción, el lado \(m\) del triángulo es

Nota: \(cos(β)\) multiplica al seno porque es la hipotenusa del triángulo.

Prolongamos el segmento \(m\) obteniendo el segmento \(p\) (el segmento \(m\) no cambia):

Observando la figura,

• El segmento \(X\) mide lo mismo que la suma de los lados \(m\) y \(p\).

• El nuevo ángulo representado mide \(\alpha\) porque junto con los ángulos \(90^\circ\) y \(90^\circ-\alpha\) debe sumar \(180^\circ \).

• Teniendo en cuenta la introducción, el lado \(p\) del triangulo superior es

  

Por tanto, el segmento \(X\) es

Como queríamos demostrar.

La demostración de esta fórmula es directa utilizando la fórmula del seno de la suma con los ángulos \(\alpha\) y \(-\beta\) y aplicando

Utilizamos la misma figura:

El segmento \(OE\) (segmento que une los puntos \(O\) y \(E\)) puede descomponerse como

Teniendo en cuenta la introducción, los segmentos implicados son

Como el lado \(b\) es \(b = sin(\beta)\),

Por tanto, la igualdad \(OE = OA+AE\) queda como

De donde, despejando,

Se demuestra utilizando la fórmula del coseno de la suma:

Y teniendo en cuenta que

Para demostrar la fórmula sólo tenemos que aplicar la definición de la tangente (seno dividido coseno).

Hacemos la demostración para la suma:

Dividimos el numerador y el denominador entre el producto \(cos(\alpha )\cdot cos(\beta )\):

---

Páginas amigas: Problemas y Ecuaciones, Ecuaciones Resueltas.