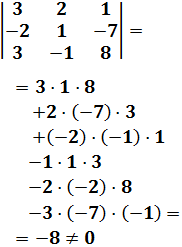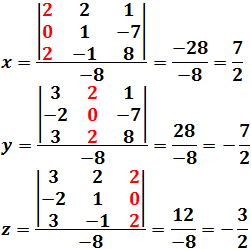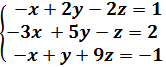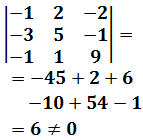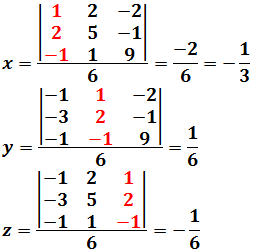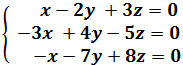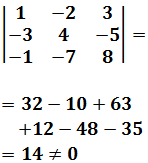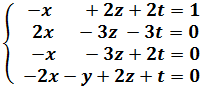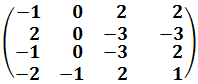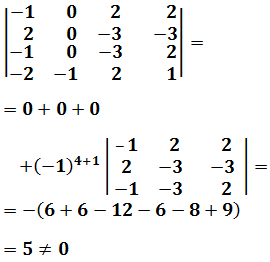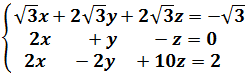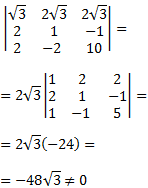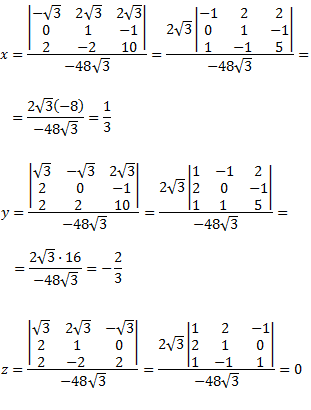Regla de Cramer
Contenido de esta página:
- Breve biografía de Gabriel Cramer
- La regla de Cramer
- Ejemplos de aplicación de la Regla de Cramer
Enlace: Calculadora online de la regla de Cramer.
Páginas relacionadas
Páginas amigas:
1. Gabriel Cramer
Gabriel Cramer, nacido en Ginebra (Suiza) en 1704, fue un matemático precoz que obtuvo el doctorado a los 18 años de edad. Fue profesor y catedrático de la Universidad de Ginebra y entre sus obras destaca Introducción al Análisis de las curvas algebraicas (1750), donde clasifica las curvas según el grado de las ecuaciones.
Es en esta obra donde reintroduce el concepto de determinantes de Leibniz (1646) y presenta el teorema ahora conocido, en su honor, como Regla de Cramer. Este teorema, la Regla de Cramer, permite, mediante la aplicación de la función determinante, la obtención inmediata de la solución de los Sistemas de Ecuaciones Compatibles Determinados, como veremos más adelante.
En 1748, dos años antes de la publicación de Cramer, Colin MacLaurin (matemático escocés) ya publicó esta regla.
La Regla de Cramer es un resultado útil y de rápida aplicación pero, sin embargo, como se ha dicho, sólo puede aplicarse en sistemas compatibles determinados.
En cambio, otro resultado mucho posterior, el Teorema de Rouché - Frobenius (del año 1875) permite la clasificación de los sitemas de ecuaciones (lineales) y los métodos de Eliminación de Gauss y de Gauss-Jordan proporcionan su solución (compatible determinado) o soluciones (compatible indeterminado).
Gabriel Cramer fallece en Bagnols-sur-Cèze (Francia) en 1752, con 46 años de edad.
2. La regla de Cramer
La regla de Cramer nos permite resolver sistemas de ecuaciones lineales (SEL) compatibles determinados, es decir, con una única solución.
El sistema tiene que ser cuadrado (tantas ecuaciones como incógnitas) y la matriz de coeficientes debe ser regular (determinante distinto de 0).
Recordad que podemos escribir el sistema de ecuaciones en forma matricial como:
$$ A·X = b $$
donde \(A\) es la matriz de coeficientes, \(X\) es la matriz columna con las incógnitas y \(b\) es la matriz columna con los términos independientes.
Bajo estas condiciones, la regla de Cramer es la siguiente:
La incógnita \(x_i\) del sistema \(AX=b\) es
$$ x_i = \frac{|A_i|}{|A|} $$
donde \(A_i\) es la matriz \(A\), pero cambiando la columna \(i\) de \(A\) por la columna de términos independientes, \(b\).
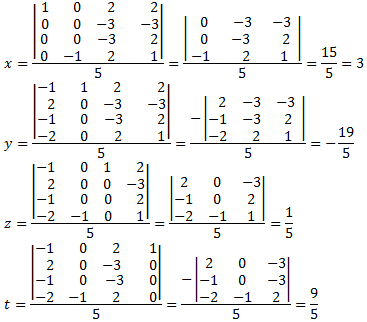
Es más fácil entender la regla viendo los ejemplos.