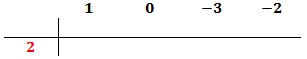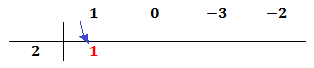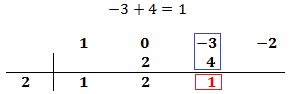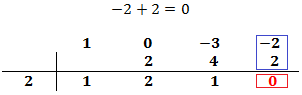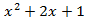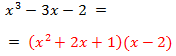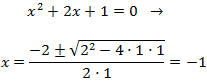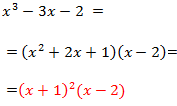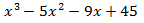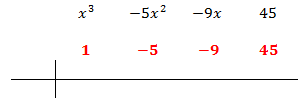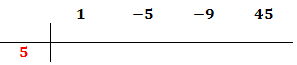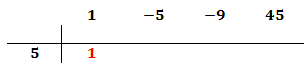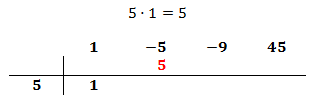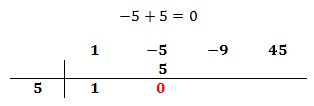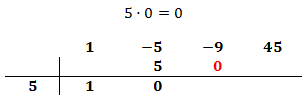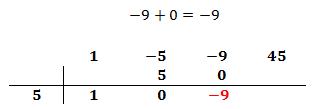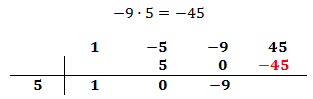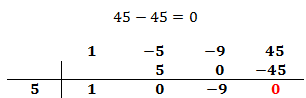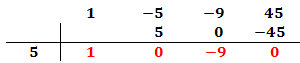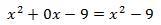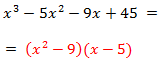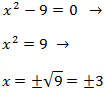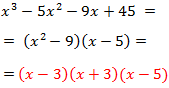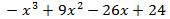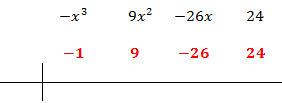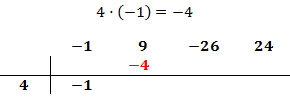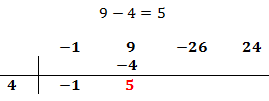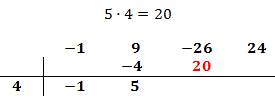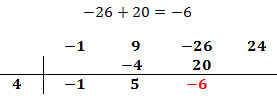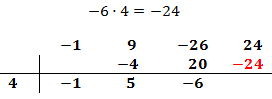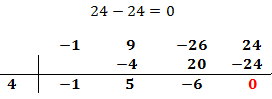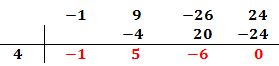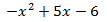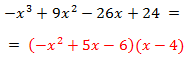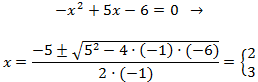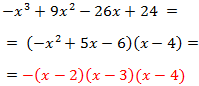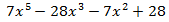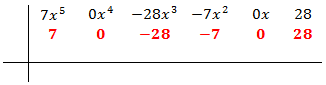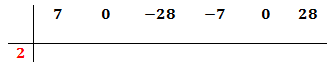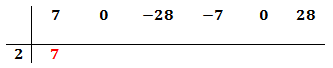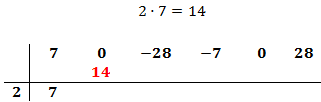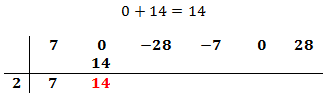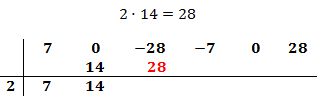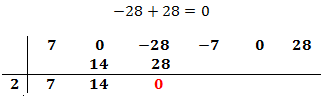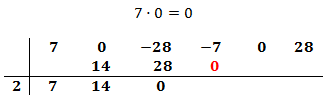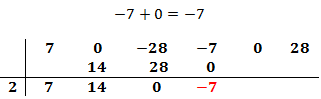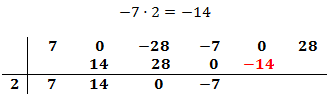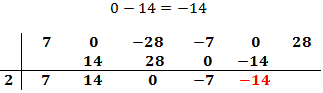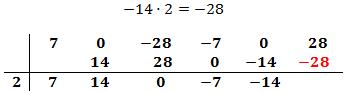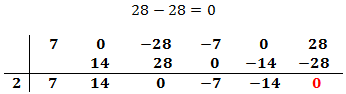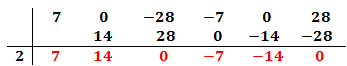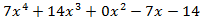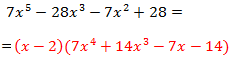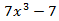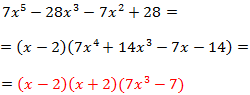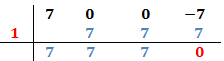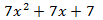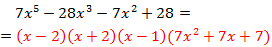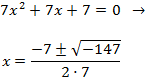Ejemplo 2
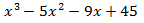
Ver solución
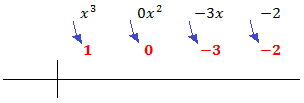
El polinomio es de grado 3.
Escribimos en la primera fila los coeficientes de cada monomio en orden decreciente de grado. Si hay algún coeficiente que sea 0 (en nuestro caso no lo hay), también hay que escribirlo.
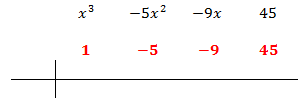
Ahora, buscamos un número que sea divisor del término independiente, es decir, del término que no tiene parte literal (ninguna x), y lo escribimos en la columna de la izquierda.
En nuestro polinomio el independiente es 45. Podemos escoger 1, -1, 3, -3, 5, -5, 9, -9.... Escogemos, por ejemplo, 5, que es divisor de 45. Si no funciona, tendremos que probar con otro hasta dar con el bueno.
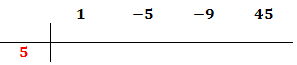
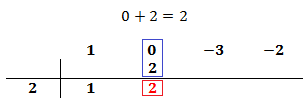
El primer coeficiente pasa a la parte inferior de la línea, sin realizar ninguna operación.
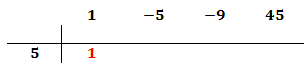
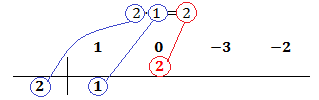
Multiplicamos el coeficiente que hemos bajado por el número de la columna izquierda y el resultado lo escribimos debajo del siguiente coeficiente, pero arriba de la línea.
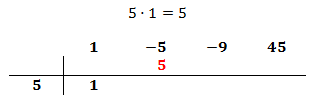
Sumamos el número que hemos escrito con el coeficiente que tiene arriba y el resultado lo escribimos debajo de la línea:
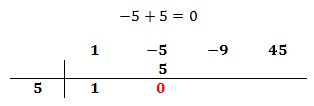
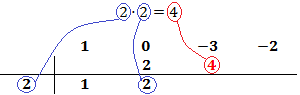
Ahora repetimos el proceso:
Multiplicamos el número obtenido por el de la columna izquierda y lo situamos debajo del siguiente coeficiente:
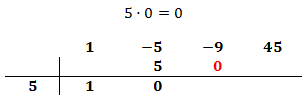
Sumamos el número que hemos escrito con el coeficiente que tiene arriba y el resultado lo escribimos debajo de la línea:
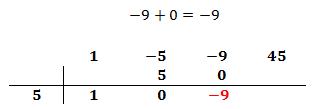
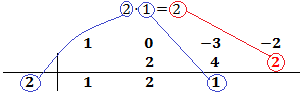
Multiplicamos el número obtenido por el de la columna izquierda y lo situamos debajo del siguiente coeficiente:
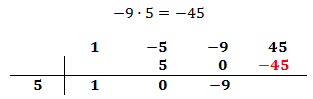
Sumamos el número que hemos escrito con el coeficiente que tiene arriba y el resultado lo escribimos debajo de la línea:
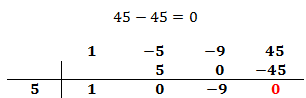
Es importante que el último número del proceso sea 0. Si no es así, significa que el número de la columna izquierda no nos sirve y debemos escoger otro.
La raíz que del polinomio que hemos calculado está en la columna izquierda.
Tenemos la raíz x = 5.
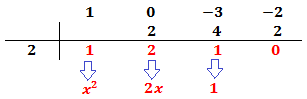
Los números de debajo de la línea son los coeficientes de un polinomio de un grado menos (en nuestro caso, de grado 2).
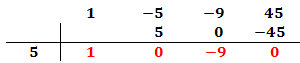
El polinomio de un grado menor es
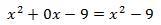
Por tanto, la primera factorización es
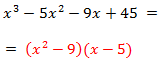
Y la raíz x = 5.
Si queremos calcular las otras raíces, aplicamos de nuevo el método al polinomio de un grado menos. En nuestro caso, como es de grado 2 e incompleto, podemos obtener las raíces inmediatamente:
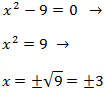
Tenemos las raíces x = -3 y x = 3.
La factorización queda
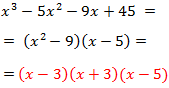
Ejemplo 3
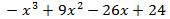
Ver solución
El polinomio es de grado 3.
Escribimos en la primera fila los coeficientes de cada monomio en orden decreciente de grado. Si hay algún coeficiente que sea 0 (en nuestro caso no lo hay), también hay que escribirlo.
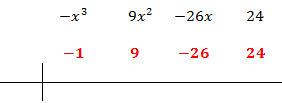
Ahora, buscamos un número que sea divisor del término independiente, es decir, del término que no tiene parte literal (ninguna x), y lo escribimos en la columna de la izquierda.
En nuestro polinomio el independiente es 24. Podemos escoger 1, -1, 2, -2, 4, -4... Escogemos, por ejemplo, 4, que es divisor de 24. Si no funciona, tendremos que probar con otro hasta dar con el bueno.
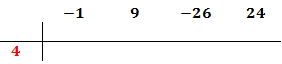
El primer coeficiente pasa a la parte inferior de la línea, sin realizar ninguna operación.
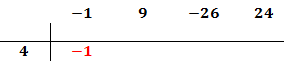
Multiplicamos el coeficiente que hemos bajado por el número de la columna izquierda y el resultado lo escribimos debajo del siguiente coeficiente, pero arriba de la línea.
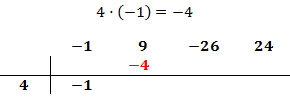
Sumamos el número que hemos escrito con el coeficiente que tiene arriba y el resultado lo escribimos debajo de la línea:
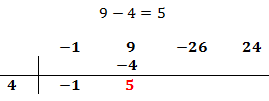
Ahora repetimos el proceso:
Multiplicamos el número obtenido por el de la columna izquierda y lo situamos debajo del siguiente coeficiente:
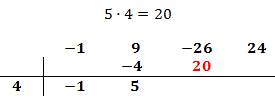
Sumamos el número que hemos escrito con el coeficiente que tiene arriba y el resultado lo escribimos debajo de la línea:
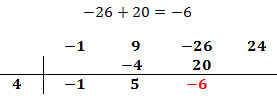
Multiplicamos el número obtenido por el de la columna izquierda y lo situamos debajo del siguiente coeficiente:
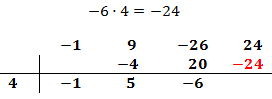
Sumamos el número que hemos escrito con el coeficiente que tiene arriba y el resultado lo escribimos debajo de la línea:
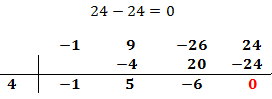
Es importante que el último número del proceso sea 0. Si no es así, significa que el número de la columna izquierda no nos sirve y debemos escoger otro.
La raíz que del polinomio que hemos calculado está en la columna izquierda.
Tenemos la raíz x = 4.
Los números de debajo de la línea son los coeficientes de un polinomio de un grado menos (en nuestro caso, de grado 2).
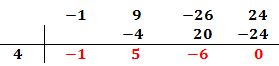
El polinomio de un grado menor es
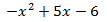
Por tanto, la primera factorización es
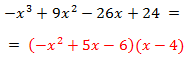
Y la raíz x = 4.
Si queremos calcular las otras raíces, aplicamos de nuevo el método al polinomio de un grado menos. En nuestro caso, como es de grado 2, usamos la fórmula para las ecuaciones cuadráticas:
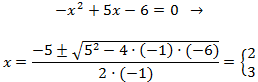
Tenemos dos raíces: x =2 y x =3.
La factorización queda
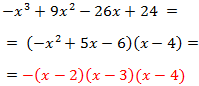
Importante: No olvidemos que al factorizar usando las raíces tenemos que multiplicar el producto de éstas por el coeficiente director del polinomio que en nuestro caso es -1.
Ejemplo 4
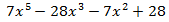
Ver solución
El polinomio es de grado 5.
Escribimos en la primera fila los coeficientes de cada monomio en orden decreciente de grado. Si hay algún coeficiente que sea 0 (en nuestro caso es el coeficiente de x4 y el de x), también hay que escribirlo.
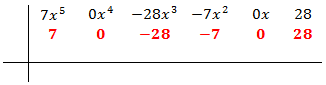
Ahora buscamos un número que sea divisor del término independiente, es decir, del término que no tiene parte literal (ninguna x), y lo escribimos en la columna de la izquierda.
En nuestro polinomio el independiente es 28. Podemos escoger 1, -1, 2, -2, 4, -4... Escogemos, por ejemplo, 2, que es divisor de 28. Si no funciona, tendremos que probar con otro hasta dar con el bueno.
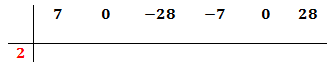
El primer coeficiente pasa a la parte inferior de la línea, sin realizar ninguna operación.
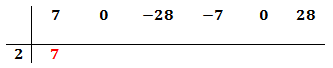
Ahora multiplicamos el coeficiente que hemos bajado por el número de la columna izquierda y el resultado lo escribimos debajo del siguiente coeficiente, pero arriba de la línea.
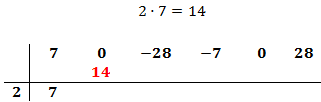
Sumamos el número que hemos escrito con el coeficiente que tiene arriba y el resultado lo escribimos debajo de la línea:
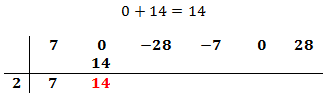
Ahora repetimos el proceso:
Multiplicamos el número obtenido por el de la columna izquierda y lo situamos debajo del siguiente coeficiente:
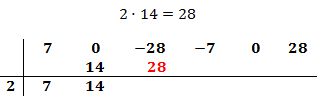
Sumamos el número que hemos escrito con el coeficiente que tiene arriba y el resultado lo escribimos debajo de la línea:
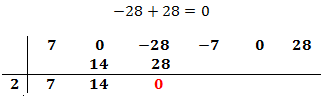
Multiplicamos el número obtenido por el de la columna izquierda y lo situamos debajo del siguiente coeficiente:
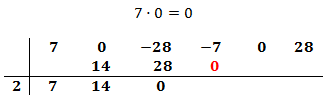
Sumamos el número que hemos escrito con el coeficiente que tiene arriba y el resultado lo escribimos debajo de la línea:
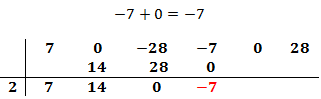
Multiplicamos el número obtenido por el de la columna izquierda y lo situamos debajo del siguiente coeficiente:
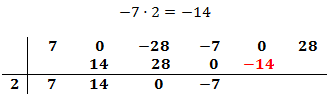
Sumamos el número que hemos escrito con el coeficiente que tiene arriba y el resultado lo escribimos debajo de la línea:
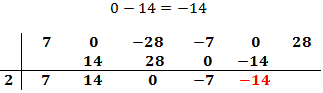
Multiplicamos el número obtenido por el de la columna izquierda y lo situamos debajo del siguiente coeficiente:
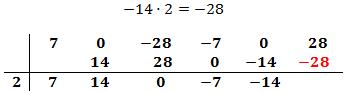
Sumamos el número que hemos escrito con el coeficiente que tiene arriba y el resultado lo escribimos debajo de la línea:
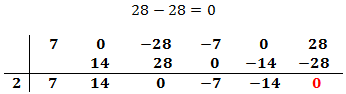
Es importante que el último número del proceso sea 0. Si no es así, significa que el número de la columna izquierda no nos sirve y debemos escoger otro.
La raíz que del polinomio que hemos calculado está en la columna izquierda.
Tenemos la raíz x = 2.
Los números de debajo de la línea son los coeficientes de un polinomio de un grado menos (en nuestro caso, de grado 4).
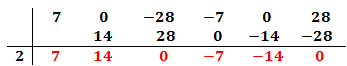
Este polinomio es
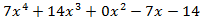
Por tanto, la primera factorización que obtenemos es
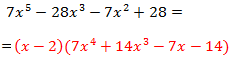
Si queremos calcular las otras raíces, aplicamos de nuevo el método al polinomio de un grado menor.

Por lo que tenemos la raíz x = -2 y el polinomio de tercer grado:
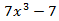
La segunda factorización es
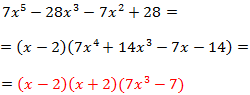
Volvemos a aplicar Ruffini:
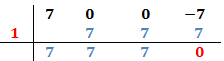
Tenemos la raíz x = 1 y el polinomio de segundo grado:
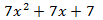
La tercera factorización es
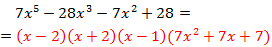
Para obtener las raíces del polinomio de segundo grado usamos la fórmula cuadrática:
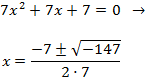
No hay raíces reales. No podemos factorizar más la expresión.