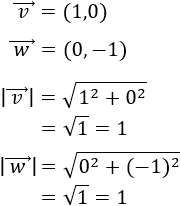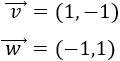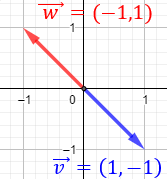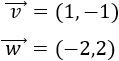Diferencias entre módulo, dirección y setido de un vector
En esta página vamos a definir y a explicar las diferencias entre el módulo, la dirección y el sentido de un vector. Como los conceptos son iguales para cualquier dimensión, trabajamos con vectores del plano real \(\mathbb{R}^2\).
Contenido de esta página:
- Introducción
- Módulo
- Sentido
- Dirección
Otros temas de vectores de \(\mathbb{R}^2\):
Páginas relacionadas
Páginas amigas:
1. Introducción
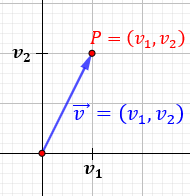
Un vector \(\vec{v}=(v_1,v_2)\) de \(\mathbb{R}^2\) es la flecha que parte del origen de coordenadas (punto \((0,0)\)) y termina en el punto \(P=(v_1,v_2)\):
Sin embargo, podemos representar el mismo vector \(\vec{v}\) partiendo de cualquier otro punto del plano, siempre y cuando tenga la misma longitud, dirección y sentido:
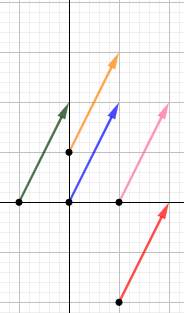
Por esta razón, es importante diferenciar estos tres conceptos: longitud (módulo), dirección y sentido.
2. Módulo
El módulo de un vector \(\vec{v}=(v_1, v_2)\) es su longitud y se denota por \(|v|\). Se calcula mediante la fórmula
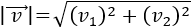
El módulo, como toda longitud, nunca puede ser negativo.
3. Sentido
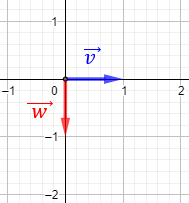
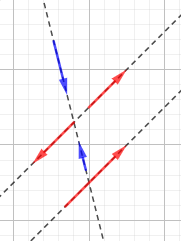
Un vector \(\vec{v}\) parte de un punto \(A\) y termina en un punto \(B\):
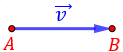
El vector \(\vec{w}\) que parte del punto \(B\) y termina en el punto \(A\) tiene sentido opuesto:
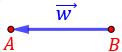
Ambos vectores unen los mismos puntos, pero en sentidos contrarios. Miden lo mismo y tienen la misma dirección.
Si el vector \(\vec{v}\) es \(\vec{v}=(v_1,v_2)\), entonces el vector \(\vec{w}\) es \(\vec{w}=(-v_1,-v_2)\). Es decir, \(\vec{w}\) es el vector opuesto de \(\vec{v}\):
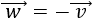
Si cambiamos el signo de las dos coordenadas de un vector, obtenemos el vector opuesto. Este vector tiene la misma dirección y el mismo módulo (longitud), pero sentido contrario.