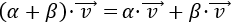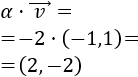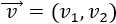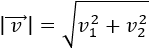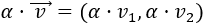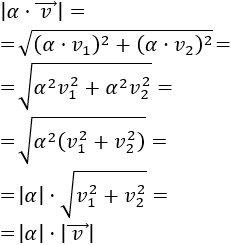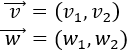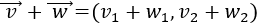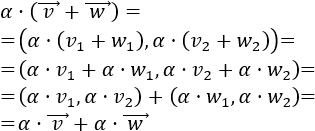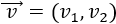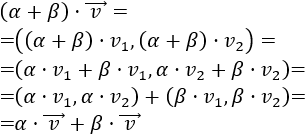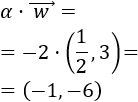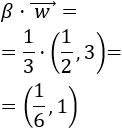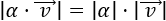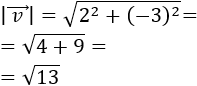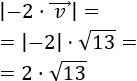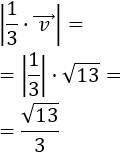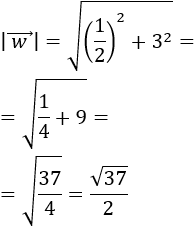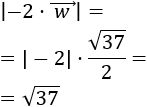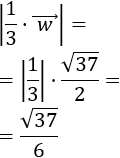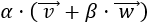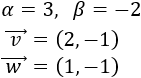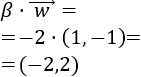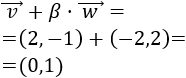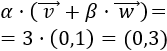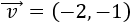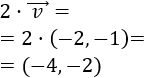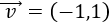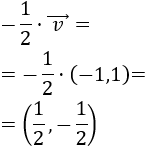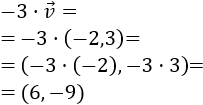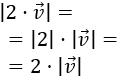Producto de un escalar por un vector del plano \(\mathbb{R}^2\)
En esta página definimos el producto de un escalar por un vector del plano \(\mathbb{R}^2\), mostramos ejemplos, demostramos las propiedades básicas y resolvemos problemas relacionados.
Nota: en esta página no vemos el producto escalar de dos vectores (ésta es otra operación).
Contenido de esta página:
- Introducción
- Definición
- Propiedades
- 9 problemas resueltos
Otros temas de vectores de \(\mathbb{R}^2\):
Páginas relacionadas
Páginas amigas:
Introducción
Recordamos que un vector \(\vec{v}\) del plano real \(\mathbb{R}^2\) es
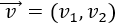
siendo \(v_1\) su primera coordenada (eje horizontal) y \(v_2\) su segunda coordenada (eje vertical):
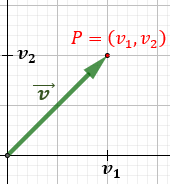
Llamamos escalar a cualquier número real \(\alpha\in\mathbb{R}\).
Definición
Dado un escalar \(\alpha \in\mathbb{R}\) y un vector \(\vec{v} = (v_1,v_2)\) de \(\mathbb{R}^2\), se define su producto como el vector
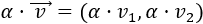
Es decir, es el vector que se obtiene al multiplicar las coordenadas del vector \(\vec{v}\) por el escalar \(\alpha\).
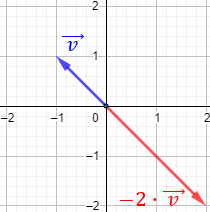
Cuando \(\alpha\neq 0\), decimos que el vector \(\alpha·\vec{v}\) es proporcional al vector \(\vec{v}\).
Propiedades
A continuación, enunciamos 7 propiedades básicas del producto de un escalar por un vector (demostramos la 5, la 6 y la 7).
Propiedad 1
Si \(\alpha > 0\), entonces el vector \(\alpha·\vec{v}\) tiene la misma dirección y sentido que \(\vec{v}\).
Propiedad 2
Si \(\alpha < 0\), entonces el vector \(\alpha·\vec{v}\) tiene la misma dirección y sentido opuesto que \(\vec{v}\).
Propiedad 3
Si \(|\alpha| > 1\), entonces la longitud del vector \(\alpha·\vec{v}\) es mayor que la de \(\vec{v}\) (tiene módulo mayor).
Propiedad 4
Si \(|\alpha| < 1\), entonces la longitud del vector \(\alpha·\vec{v}\) es menor que la de \(\vec{v}\) (tiene módulo menor).
Propiedad 5
Más exactamente, el módulo del \(\alpha·\vec{v}\) cumple
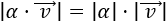
Propiedad 6
El producto es distributivo respecto de la suma de vectores:
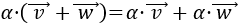
Propiedad 7
El producto es distributivo respecto de la suma de escalares: