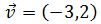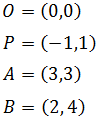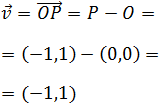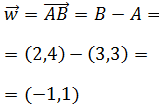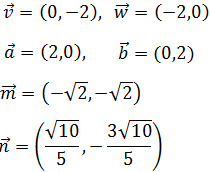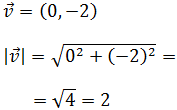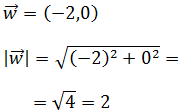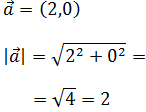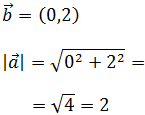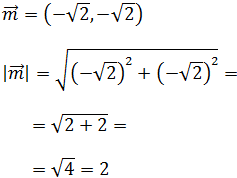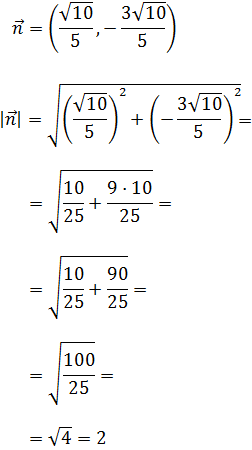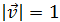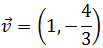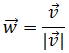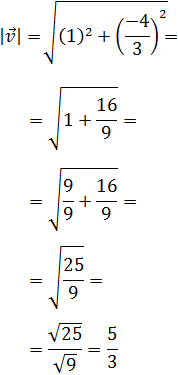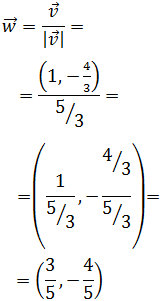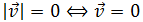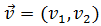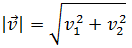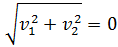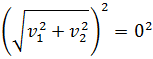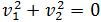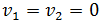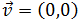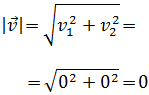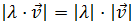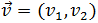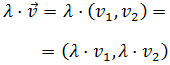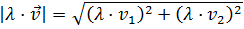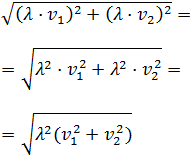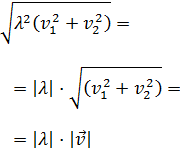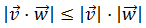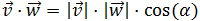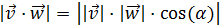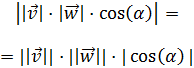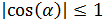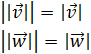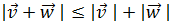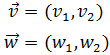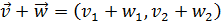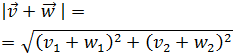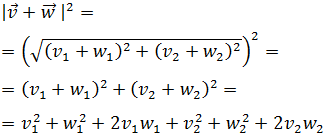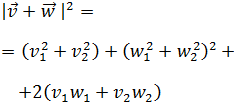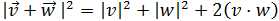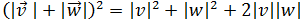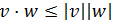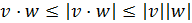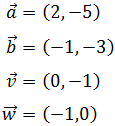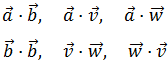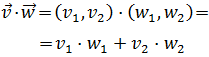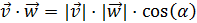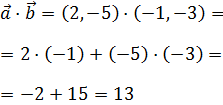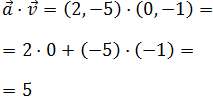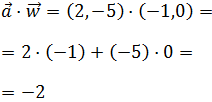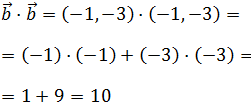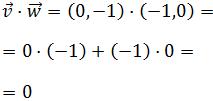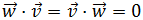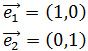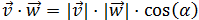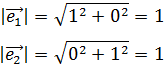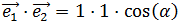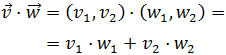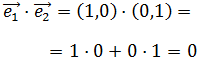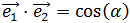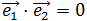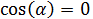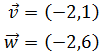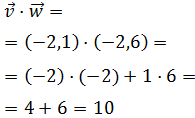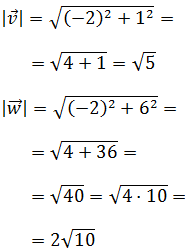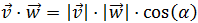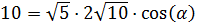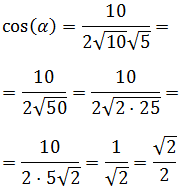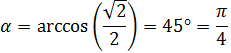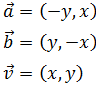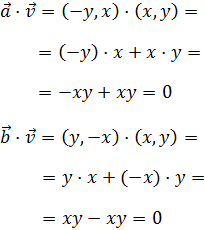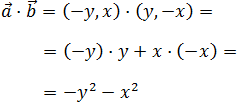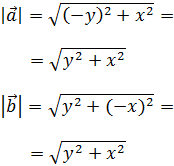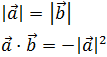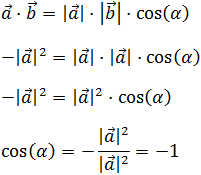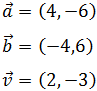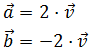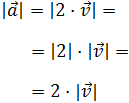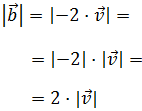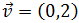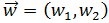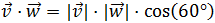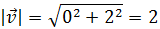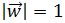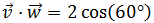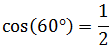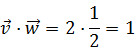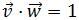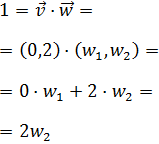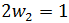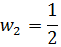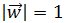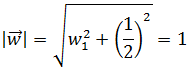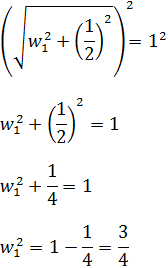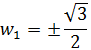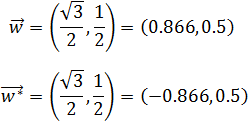Problema 1
Sean los vectores
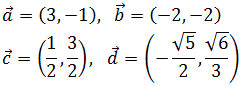
Calcular las siguientes sumas y restas:
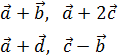
Ver solución
La suma se calcula sumando coordenada a coordenada:
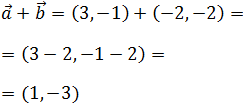
En la siguiente suma tenemos el producto de un vector por un escalar.
El escalar pasa multiplicando a las dos coordenadas del vector:
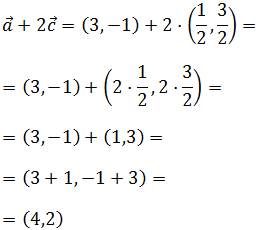
La siguiente suma es
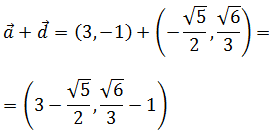
Podemos calcular la resta \(\vec{c}-\vec{b}\) como una suma de vectores:
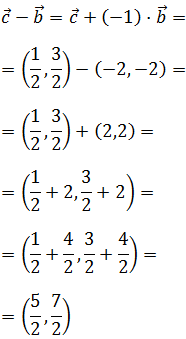
Problema 2
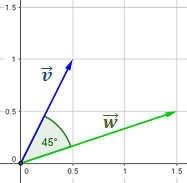
Sean los vectores
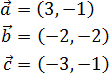
Calcular, geométricamente, las siguientes sumas y restas de vectores:
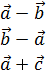
Ver solución
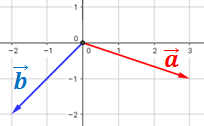
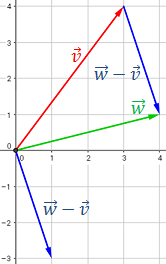
Representamos los vectores 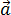 y
y
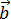 :
:
La resta 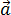 -
- 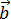 es el vector que une los extremos de los vectores con el sentido de
es el vector que une los extremos de los vectores con el sentido de
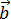 a
a 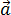 :
:
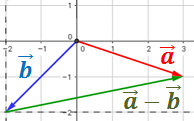
Calculamos sus coordenadas: para ello,
dibujamos unos ejes cuyo origen sea donde comienza el vector.
En el eje de las abscisas (eje horizontal) el vector ocupa 5
unidades; en el de ordenadas ocupa 1 unidad. Por tanto, el vector es
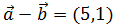
La resta
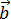 -
- 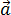 es el vector que une los extremos de los vectores con el sentido de
es el vector que une los extremos de los vectores con el sentido de
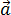 a
a 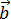 . Para calcular las coordenadas, dibujamos unos ejes cuyo origen es el origen del vector:
. Para calcular las coordenadas, dibujamos unos ejes cuyo origen es el origen del vector:
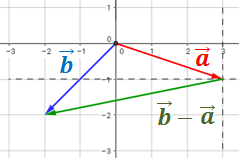
Por tanto, el vector es
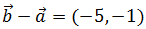
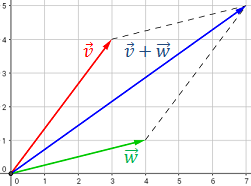
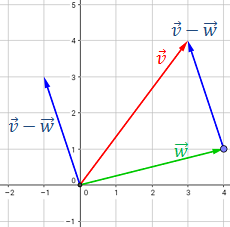
Para calcular la siguiente suma, representamos los vectores
y dibujamos segmentos paralelos a los vectores y que
pasen por los extremos de los vectores:
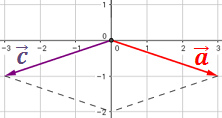
El vector suma comienza en el origen y termina en la intersección de los segmentos:
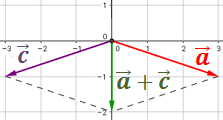
Por tanto, el vector es
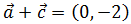
Observad que se cumple
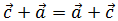
Esto se debe a que la suma de vectores es conmutativa (por serlo la suma de los reales).
Problema 3
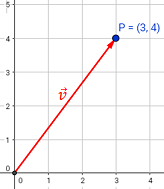
Sean los puntos
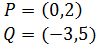
Encontrar el vector que va de P a Q y el vector que va de Q a P.
Ver solución
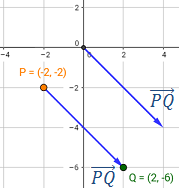
El vector que va de P a Q es
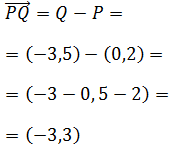
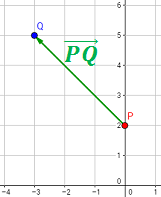
Representación:
El vector que va de Q a P es
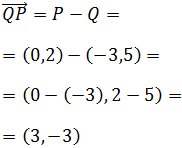
Representación:
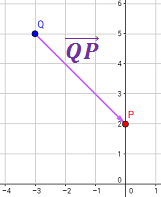
Observad que el vector \(\vec{QP}\) es el vector opuesto a \(\vec{PQ}\), es decir, \(\vec{QP} = -\vec{PQ}\). Tienen la misma dirección y la misma longitud, pero sentido opuesto.
Problema 4
Sean los puntos
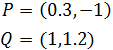
Encontrar el vector que va de P a Q y el vector que va de Q a P.
Ver solución
El vector que va de P a Q es
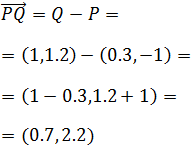
Representación:
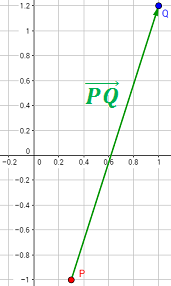
Por lo que vimos en el ejercicio anterior, para calcular el otro vector es suficiente
multiplicar el vector anterior por el escalar -1 para cambiar su sentido:
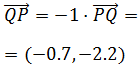
Problema 5
Sean los puntos
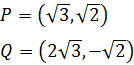
Encontrar el vector que va de P a Q y el vector que va de Q a P.
Ver solución
El vector que va de P a Q es
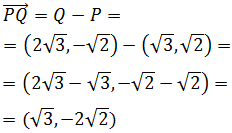
Para calcular el otro vector es suficiente
multiplicar el vector anterior por el escalar -1 para cambiar su sentido:
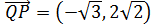
Problema 6
Sea el vector
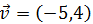
Obtener el vector igual a
 pero con sentido contrario.
pero con sentido contrario.
Ver solución
Para obtener el mismo vector pero con sentido contrario sólo tenemos
que multiplicar por el escalar -1:
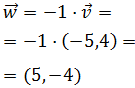
Problema 7
Sea el vector
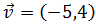
Obtener el vector simétrico de
 respecto del eje de abscisas.
respecto del eje de abscisas.
Ver solución
El eje de las abscisas es el horizontal.
Para tener una simetría respecto de este eje, la
primera coordenada debe ser la misma.
Cambiamos el signo a la segunda y tenemos el vector simétrico:
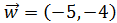
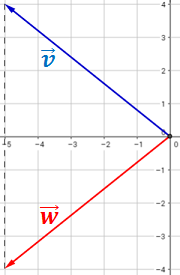
Representación:
Problema 8
Sea el vector
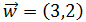
Obtener el vector simétrico de
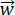 respecto del eje de ordenadas.
respecto del eje de ordenadas.
Ver solución
Como la simetría es respecto del eje vertical, tenemos que
cambiar el signo a la primera coordenada del vector:
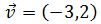
Representación:
Problema 9
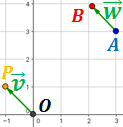
Encontrar el vector
 que va del punto
O al punto P y el vector
que va del punto
O al punto P y el vector
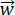 que va del punto A al punto B:
que va del punto A al punto B:
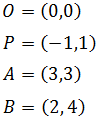
Explicar la relación existente entre ambos vectores.
Ver solución
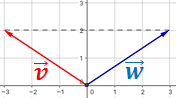
El vector que va de O a P es
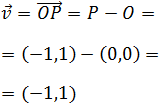
El vector que va de A a B es
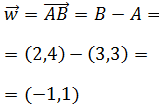
Ambos vectores son el mismo vector porque tienen las mismas coordenadas, aunque están situados en distintos lugares del plano.
Si estamos en el punto O y nos movemos una unidad a la izquierda y
una unidad hacia arriba, entonces llegamos al punto P.
Si estamos en el punto A y realizamos los mismos movimientos,
llegamos al punto B.
Problema 10
Calcular el módulo de los siguientes vectores del plano:
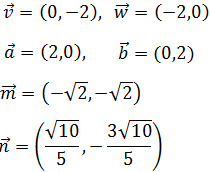
¿Un vector queda determinado por su módulo? Es decir,
si dos vectores tienen el mismo módulo, ¿son el mismo vector?
Ver solución
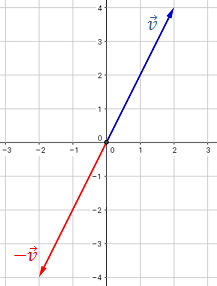
Recordemos que el módulo de un vector
\(\vec{v}=(v_1,v_2)\) es
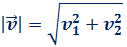
Calculamos el módulo del primer vector:
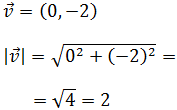
Calculamos el módulo del segundo vector:
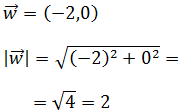
Calculamos el módulo del tercer vector:
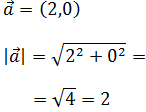
Calculamos el módulo del cuarto vector:
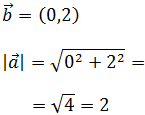
Calculamos el módulo del quinto vector:
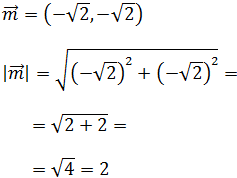
Calculamos el módulo del sexto vector:
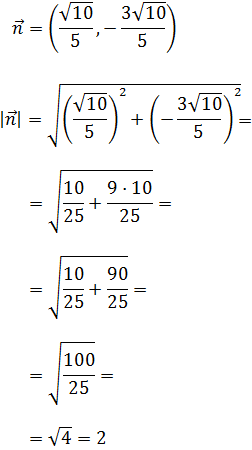
Observad que el módulo de todos los
vectores es 2. Es por ello que, al representar
los vectores partiendo desde el origen, todos terminan en la circunferencia
de radio 2:
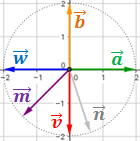
Como vemos en este ejercicio, existen muchos vectores con el mismo módulo. Hay infinitos vectores con módulo igual a 2. Por consiguiente, el módulo no es suficiente para determinar un vector.
Problema 11
¿Cuántos vectores unitarios
existen? Los vectores unitarios son los que cumplen que su módulo es 1:
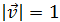
Ver solución
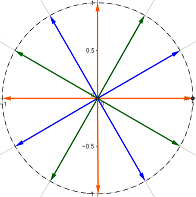
Existen infinitos vectores cuyo módulo es la unidad.
Consideremos la circunferencia de radio 1, entonces existe un vector unitario
por cada uno de sus puntos (del origen al punto):
Problema 12
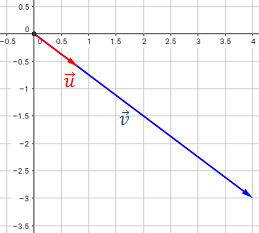
Calcular un vector que sea unitario (módulo 1) y tenga la misma dirección y
sentido que
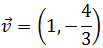
¿Existen más vectores unitarios con la misma dirección y sentido que el vector
 ?
?
Ver solución
El único vector con la misma dirección
y sentido que
 lo podemos encontrar dividiendo las
coordenadas del vector
lo podemos encontrar dividiendo las
coordenadas del vector
 por su módulo (siempre que su módulo no sea 0):
por su módulo (siempre que su módulo no sea 0):
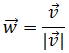
Calculamos el módulo de
 :
:
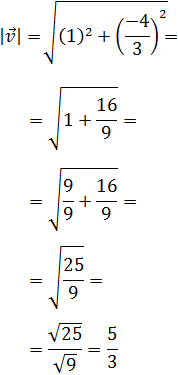
Por tanto, el vector unitario (con el mismo sentido y dirección que  ) es
) es
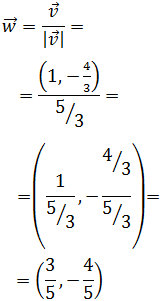
Problema 13
Sea
 un vector cualquiera, demostrar que:
un vector cualquiera, demostrar que:
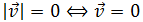
Es decir, el módulo de un vector es 0 sólo si es el vector nulo
$$ v = (0,0) $$
y si
 es el vector nulo, entonces su módulo es 0.
es el vector nulo, entonces su módulo es 0.
Ver solución
Las coordenadas del vector son
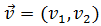
Su módulo es
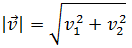
Supongamos que el módulo del vector es 0, entonces
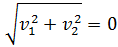
Elevamos al cuadrado:
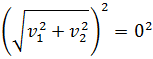
Entonces,
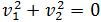
Recordad que todo número real
al cuadrado es 0 ó un número positivo.
Como tenemos que la suma de los dos cuadrados es 0,
necesariamente los dos sumandos han de ser 0, es decir,
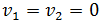
Por tanto, el vector es el vector nulo:
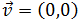
Falta demostrar que el módulo del vector nulo es 0,
pero esto es inmediato ya que
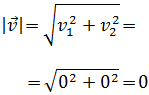
Problema 14
Sea
 un vector cualquiera y λ un número real (un escalar), demostrar que:
un vector cualquiera y λ un número real (un escalar), demostrar que:
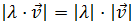
Ver solución
Si las coordenadas del vector son
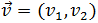
Entonces, al multiplicar por el escalar tenemos que
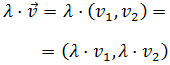
Por tanto, el módulo del producto es
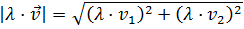
Aplicamos las propiedades de las potencias:
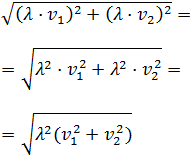
Podemos extraer el escalar de la raíz ya que está al cuadrado,
pero como no sabemos si es positivo o negativo, tenemos que
extraerlo con valor absoluto:
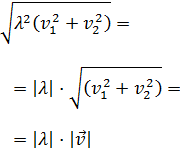
Queda demostrado que
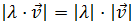
Problema 15
Sean
 y
y
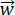 dos vectores arbitrarios. Demostrar que
dos vectores arbitrarios. Demostrar que
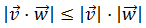
El producto de la izquierda es el producto escalar
de dos vectores; el producto de la derecha es el producto de los
números reales. En la izquierda, las barras son
un valor absoluto; en la derecha, las barras son los módulos.
Ver solución
Tenemos dos formas de calcular el producto
escalar de dos vectores: multiplicando las coordenadas
o multiplicando
los módulos y el coseno del ángulo. Usaremos la segunda:
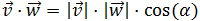
Por tanto, el valor absoluto de la expresión anterior es
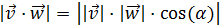
Usamos la propiedad: el valor absoluto
de un producto es el producto de los valores absolutos:
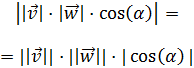
Finalmente, sabemos que el coseno está entre -1 y 1, por tanto
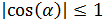
Además, como el módulo de un vector es siempre no negativo
(es una raíz cuadrada), se cumple que
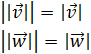
Luego queda demostrado que
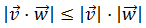
Problema 16
Sean
 y
y
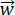 dos vectores arbitrarios. Demostrar que
dos vectores arbitrarios. Demostrar que
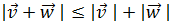
Ver solución
Sean los vectores
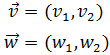
La suma de los vectores es
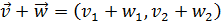
Luego el módulo de la suma es
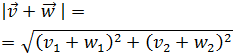
Elevamos al cuadrado:
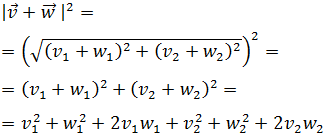
Reagrupamos los sumandos
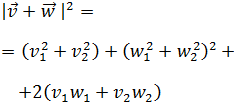
Notemos que en la expresión anterior tenemos los módulos de los vectores
al cuadrado y el producto escalar de vectores.
Así que
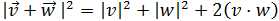
Por otro lado, la suma de los dos módulos de los vectores al cuadrado es
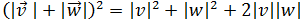
Es suficiente demostrar que
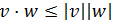
Pero esto es cierto ya que si aplicamos la propiedad del ejercicio 15,
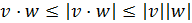
Problema 17
Sean los vectores
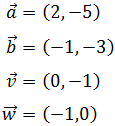
Calcular los siguientes productos escalares:
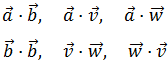
Ver solución
Recordamos que podemos calcular el producto escalar
de dos vectores de dos formas distintas: multiplicando sus coordenadas:
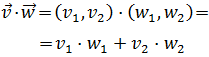
O multiplicando sus módulos por el coseno del ángulo α que forman:
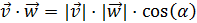
En este ejercicio, como conocemos las coordenadas,
usaremos la primera de las fórmulas.
El primer producto es
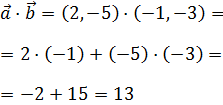
El segundo producto es
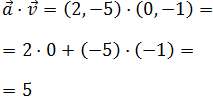
El tercer producto es
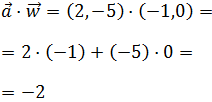
El cuarto producto es
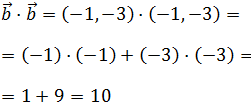
El quinto producto es
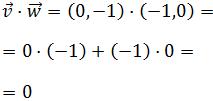
Por último, sexto producto es
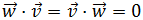
porque el producto escalar de vectores es una operación conmutativa.
Problema 18
Calcular, mediante las fórmulas del producto escalar, el ángulo que forman los vectores canónicos del plano, es decir,
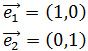
Los llamamos así porque son los vectores de la base canónica del plano.
Ver solución
Primero usaremos la siguiente fórmula del producto escalar
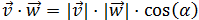
Calculamos los módulos de los vectores:
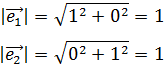
Por tanto, aplicando la fórmula del producto escalar
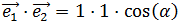
Usamos la otra fórmula del producto escalar:
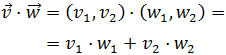
Luego
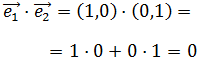
Entonces, tenemos, por un lado
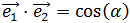
Y por otro,
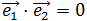
Luego, igualando,
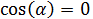
Sabemos que si el coseno del ángulo es 0, entonces el ángulo es

(expresado en grados y en radianes).
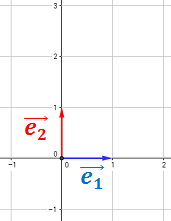
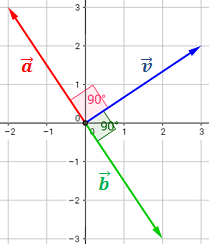
Estos vectores están situados sobre los ejes de coordenadas, es por ello que son perpendiculares:
Problema 19
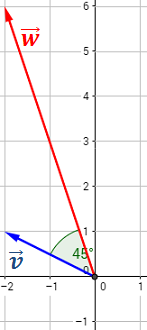
Calcular el ángulo que forman los vectores
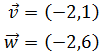
Ver solución
Por una lado, el producto escalar de los vectores es
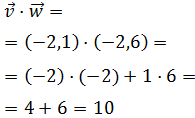
Calculamos los módulos
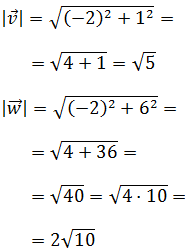
Aplicamos la fórmula del producto escalar en la que aparece el coseno:
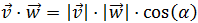
De la fórmula conocemos los módulos y el producto. Sustituyendo:
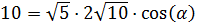
Aislamos el coseno:
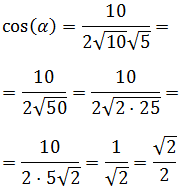
Finalmente, para calcular el ángulo tenemos que utilizar la función arcocoseno:
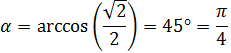
Hemos expresado el ángulo en grados y en radianes.
Problema 20
Demostrar que los vectores
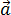 y
y
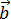 son perpendiculares a
son perpendiculares a
 :
:
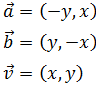
Además, demostrar que los vectores
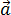 y
y
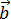 son paralelos entre sí.
son paralelos entre sí.
Se supone que
$$ x,y \neq 0 $$
Ver solución
Si los vectores son perpendiculares al vector
 ,
entonces forman un ángulo recto con dicho vector. El coseno de dicho ángulo
es 0:
,
entonces forman un ángulo recto con dicho vector. El coseno de dicho ángulo
es 0:

Entonces, los productos escalares de los vectores tienen que ser 0.
En efecto, los productos escalares son
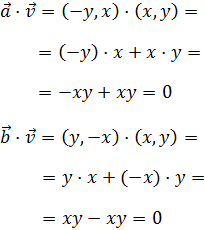
Por otro lado, el producto escalar de los vectores
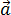 y
y
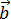 es
es
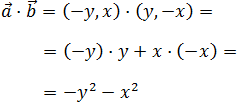
Los módulos de estos dos vectores son
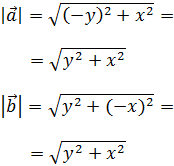
Notemos que se cumplen las siguientes igualdades:
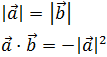
Por tanto, aplicando la fórmula del producto escalar
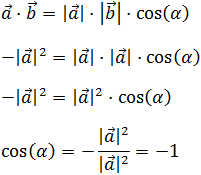
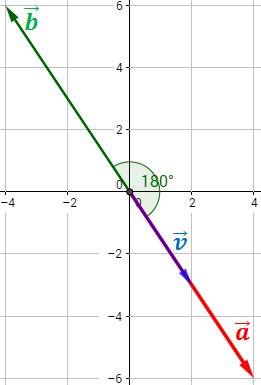
Como el coseno del ángulo es -1, entonces el
ángulo es α = 180°. Esto quiere decir que los vectores
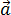 y
y
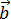 tienen la misma dirección pero sentidos opuestos. Como consecuencia, son paralelos (el
hecho de que tengan sentidos opuestos no es significante ya que lo que nos interesa
es la dirección).
tienen la misma dirección pero sentidos opuestos. Como consecuencia, son paralelos (el
hecho de que tengan sentidos opuestos no es significante ya que lo que nos interesa
es la dirección).
Problema 21
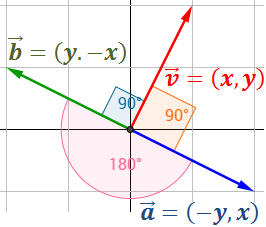
Demostrar que los vectores
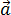 y
y
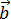 son paralelos a
son paralelos a
 :
:
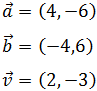
Si ambos son paralelos, ¿por qué el ángulo que forman con
 es distinto?
es distinto?
Ver solución
Si dos vectores son paralelos, el ángulo que forman
es de 0 grados ó 180 grados. Por tanto, su producto
escalar tiene que ser 1 ó -1.
En vez de calcular el producto escalar, observemos
que los tres vectores son proporcionales:
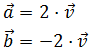
El vector
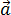 tiene la misma dirección y sentido que
tiene la misma dirección y sentido que
 .
La diferencia es que su módulo es el doble:
.
La diferencia es que su módulo es el doble:
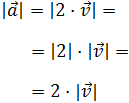
El vector
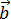 tiene la misma dirección que
tiene la misma dirección que
 pero sentido opuesto. Su módulo también es el doble:
pero sentido opuesto. Su módulo también es el doble:
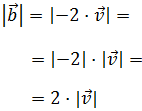
Como los tres vectores tienen la misma dirección,
son paralelos. El vector
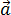 forma un ángulo de 0 grados
porque tiene el mismo sentido que
forma un ángulo de 0 grados
porque tiene el mismo sentido que
 ,
mientras que el vector
,
mientras que el vector
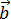 forma un ángulo de 180 grados porque tiene sentido opuesto.
forma un ángulo de 180 grados porque tiene sentido opuesto.
Problema 22
Encontrar el vector unitario que forma un ángulo de 60 grados con el vector
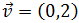
Ver solución
El vector que buscamos es
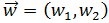
El producto escalar de los vectores es
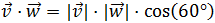
El módulo del vector
 es
es
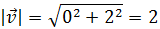
Tenemos que exigir que el vector sea unitario:
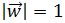
De este modo, la fórmula del producto escalar queda como
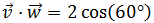
El coseno del ángulo es
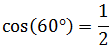
Luego la fórmula queda como
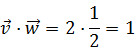
Es decir,
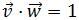
Calculamos el producto escalar multiplicando las coordenadas de los vectores:
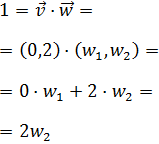
Por tanto, tenemos la ecuación de primer grado
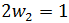
Cuya solución proporciona la segunda coordenada del vector:
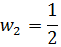
Para obtener la primera coordenada usamos la ecuación
que nos proporciona haber exigido que el vector sea unitario:
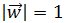
Entonces,
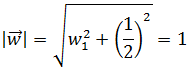
Elevamos al cuadrado ambos lados de la igualdad:
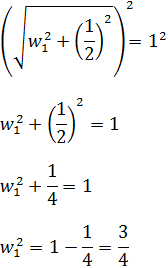
No olvidemos que al hacer la raíz cuadrada tenemos que escribir los dos signos:
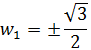
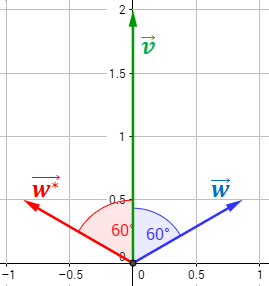
Hemos obtenido dos vectores que forman dicho ángulo (por un lado y por el otro):
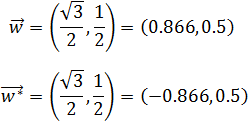


Vectores del plano real -
© matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.
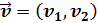
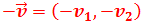
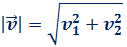
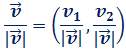
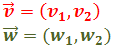
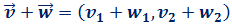
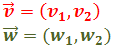

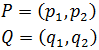
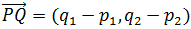
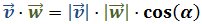
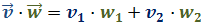

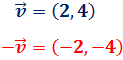
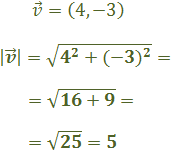
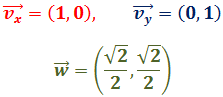
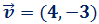
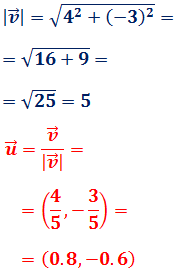
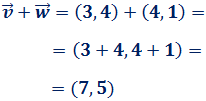
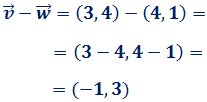
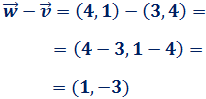
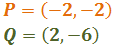
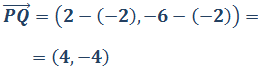
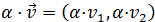
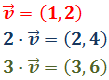
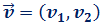
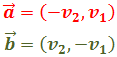
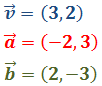
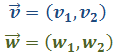
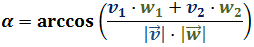
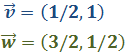
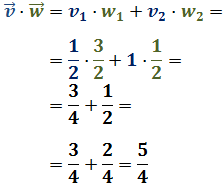
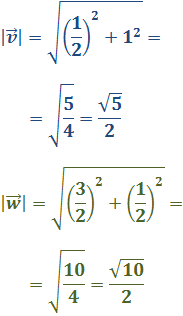
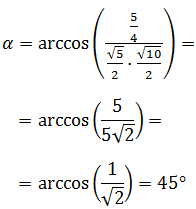
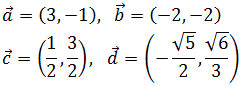
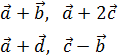
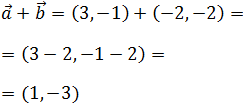
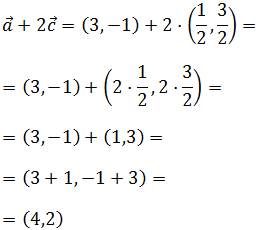
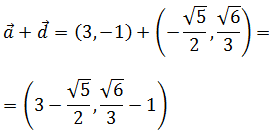
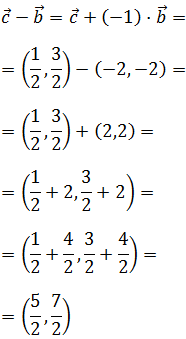
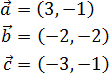
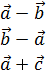
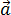 y
y
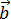 :
:

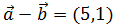

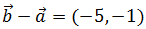


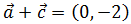
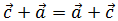
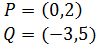
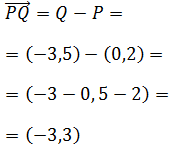

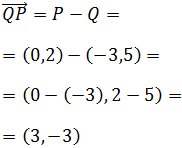

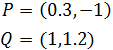
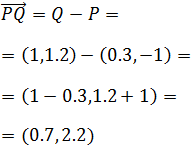

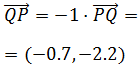
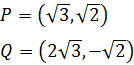
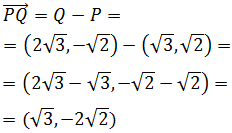
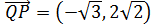
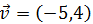
 pero con sentido contrario.
pero con sentido contrario.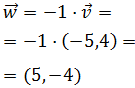
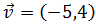
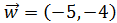

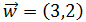
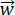 respecto del eje de ordenadas.
respecto del eje de ordenadas.