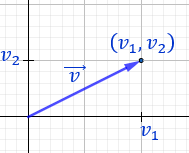
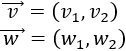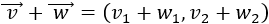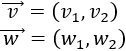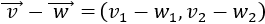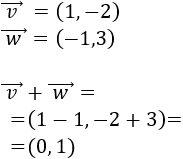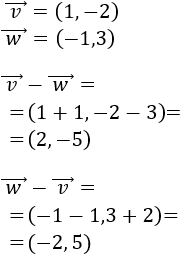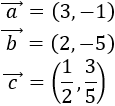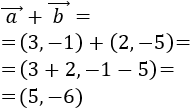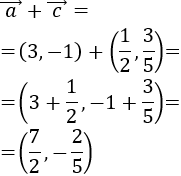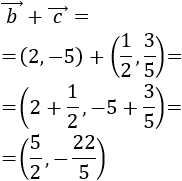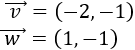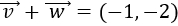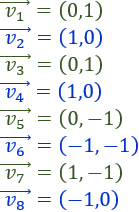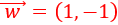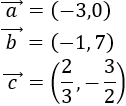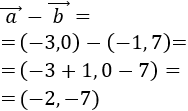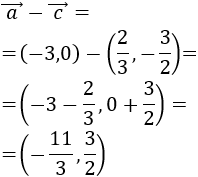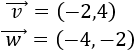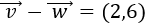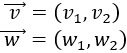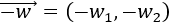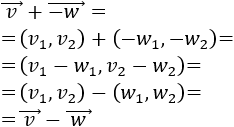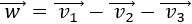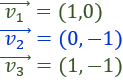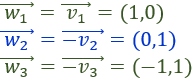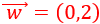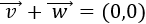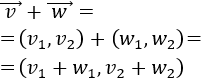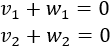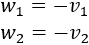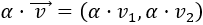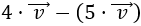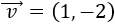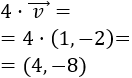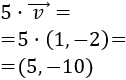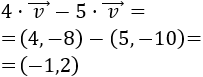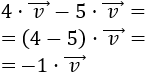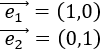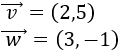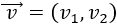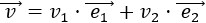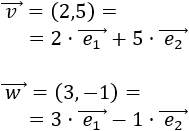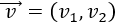Problema 1
Calcular analíticamente las sumas de vectores \(\vec{a}+\vec{b}\), \(\vec{a}+\vec{c}\) y \(\vec{b}+\vec{c}\), donde
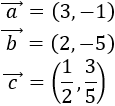
Ver solución
Calculamos la suma \(\vec{a}+\vec{b}\):
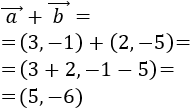
Calculamos la suma \(\vec{a}+\vec{c}\):
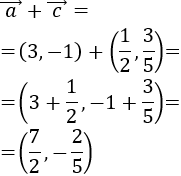
Calculamos la suma \(\vec{b}+\vec{c}\):
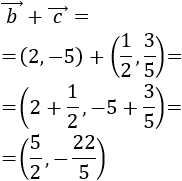
Problema 2
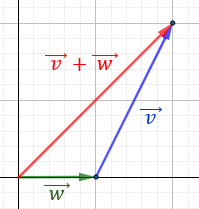
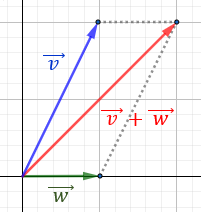
Sumar geométricamente los siguientes dos vectores:
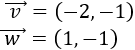
Ver solución
Representamos el vector \(\vec{w}\) partiendo desde el punto final del vector \(\vec{v}\):
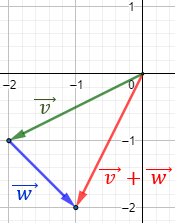
Observando la representación, el vector suma es
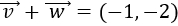
Problema 3
Calcular geométricamente la suma de los siguientes 8 vectores:
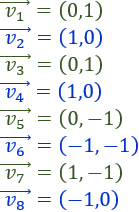
Ver solución
Representamos el vector \(\vec{v_1}\) partiendo del origen y el vector \(\vec{v_{i+1}}\) partiendo del final del vector \(\vec{v_i}\):
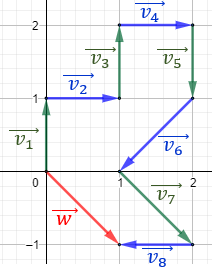
La suma de todos los vectores es el vector \(\vec{w}\) que parte del origen de \(\vec{v_1}\) y termina en el final de \(\vec{v_8}\).
A partir de la representación, la suma de los vectores es
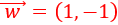
Problema 4
Calcular analíticamente las restas de vectores \(\vec{a}-\vec{b}\), \(\vec{a}-\vec{c}\) y \(\vec{b}-\vec{c}\), donde
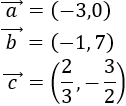
Ver solución
Calculamos la resta \(\vec{a}-\vec{b}\):
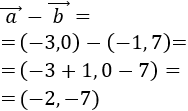
Calculamos la resta \(\vec{a}-\vec{c}\):
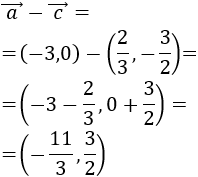
Calculamos la resta \(\vec{b}-\vec{c}\):
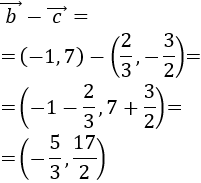
Problema 5
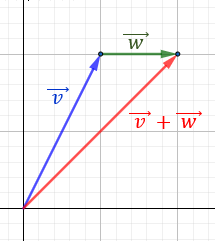
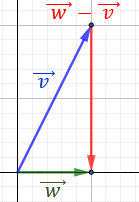
Calcular geométricamente la resta de vectores \(\vec{v}-\vec{w}\), donde
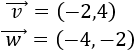
Ver solución
Representamos los dos vectores. El vector resta \(\vec{v}-\vec{w}\) es el vector va desde el final de \(\vec{w}\) hasta el final de \(\vec{v}\):
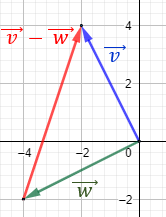
Observando la representación, el vector obtenido es
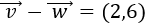
Nota: hemos representado el plano con escala de 2 unidades.
Problema 6
Sean los vectores
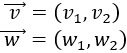
Comprobar que la resta \(\vec{v}-\vec{w}\) es igual a la suma \(\vec{v}+ \vec{-w} \), siendo \(\vec{-w} \) el vector opuesto de \(\vec{w}\), es decir,
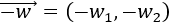
Nota: el vector \(\vec{-w}\) tiene la misma dirección y longitud que \(\vec{w}\), pero sentido contrario.
Ver solución
Calculamos la suma de los vectores \(\vec{v}+ \vec{-w} \) sumando sus coordenadas:
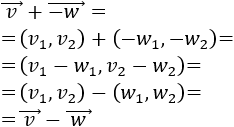
Problema 7
Calcular geométricamente la siguiente resta de vectores:
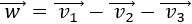
siendo los vectores
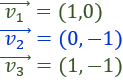
Ayuda: utilizar el problema anterior.
Ver solución
Es más sencillo sumar geométricamente que restar. Si utilizamos el problema anterior, tenemos que sumar los siguientes vectores:
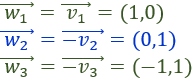
Sumamos geométricamente:
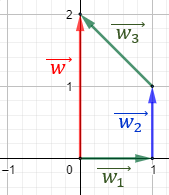
Observando la representación, la resta de vectores es
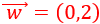
Problema 8
Dado un vector \(\vec{v}\), calcular el único vector \(\vec{w}\) que cumple
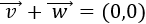
Ver solución
Supongamos que tenemos los vectores
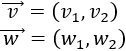
Calculamos su suma:
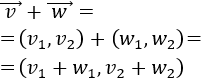
Para que la suma sea el vector de ceros, tienen que cumplirse las ecuaciones
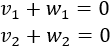
Por tanto, las coordenadas del vector \(\vec{w}\) tienen que ser
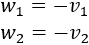
Se trata del vector opuesto a \(\vec{v}\).
Problema 9
Sea \(\alpha\) un número real cualquiera (llamado escalar) y sea \(\vec{v} = (v_1,v_2)\) un vector, se define el producto del escalar \(\alpha \) por el vector \(\vec{v}\) como el vector
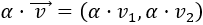
Calcular la siguiente operación:
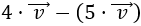
donde
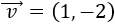
Ver solución
Calculamos el producto \(4·\vec{v}\):
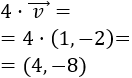
Calculamos el producto \(5·\vec{v}\):
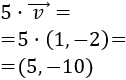
Restamos los vectores:
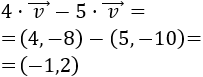
Observad que se cumple
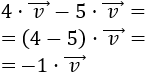
Problema 10
Todo vector del plano puede escribirse como combinación lineal de los vectores canónicos \(\vec{e_1}\) y \(\vec{e_2}\), siendo
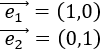
Escribir los siguientes vectores como combinación lineal de los canónicos:
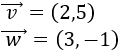
Ver solución
Un vector cualquiera del plano es
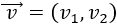
Podemos escribir este vector como
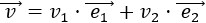
Descomponemos los vectores del problema:
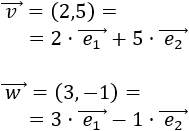
Problema 11
En este problema vamos a ver los vectores como desplazamientos.
Sea el vector
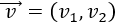
Podemos ver las coordenadas del vector como el desplazamiento de \(v_1\) unidades en dirección horizontal y \(v_2\) unidades en dirección vertical.
-
Si la primera coordenada es positiva, el desplazamiento es hacia la derecha. Si no, hacia la izquierda.
-
Si la segunda coordenada es positiva, el desplazamiento es hacia arriba. Si no, hacia abajo.
Determinar el punto en el que nos encontraremos si, partiendo del punto (2,2) del plano, realizamos los siguientes desplazamientos:
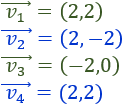
¿Qué operación vectorial hemos realizado durante el desplazamiento? ¿Cuál es el punto final si el desplazamiento comienza en el punto (-1,5)?
Ver solución
Representamos el primer vector en el punto inicial del desplazamiento y los siguientes vectores, en el final del vector que le precede:
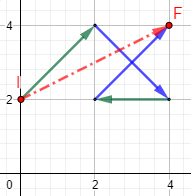
El punto final es (4,4).
La operación vectorial es la suma de los 4 vectores. El resultado de la suma es el vector (en rojo)
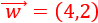
Si comenzamos en el punto (-1,5), terminamos en el punto (3,7). Lo sabemos porque es donde apunta el vector \(\vec{w}\) si lo colocamos en el punto (-1,5).


Sumar y restar vectores del plano -
© matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.