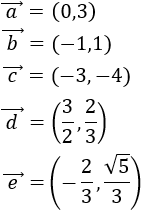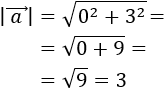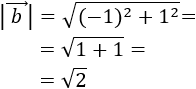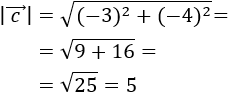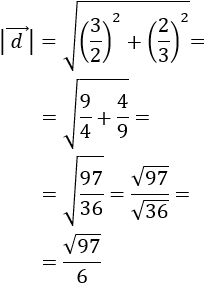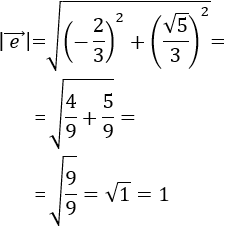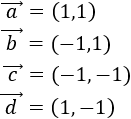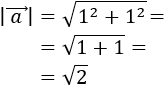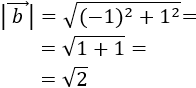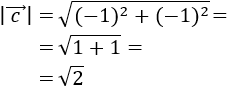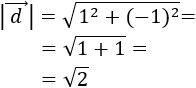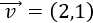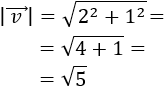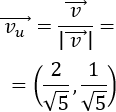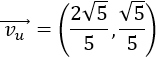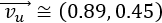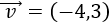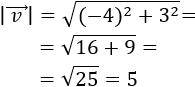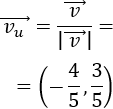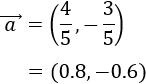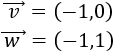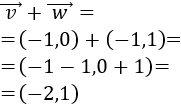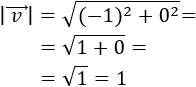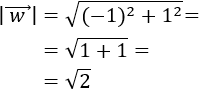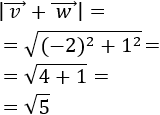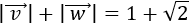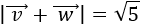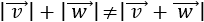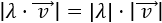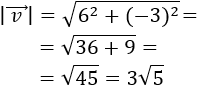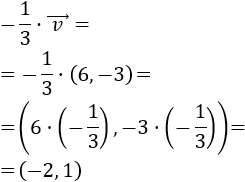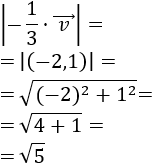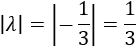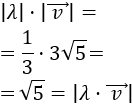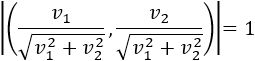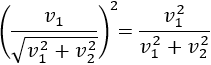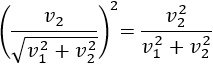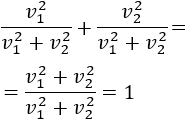Módulo de un vector del plano \(\mathbb{R}^2\)

Dedicamos esta página al módulo de los vectores del plano real \(\mathbb{R}^2\). Definimos el módulo, proporcionamos ejemplos, explicamos su significado y propiedades y resolvemos problemas relacionados.

Contenido de esta página:

1. Introducción
2. Módulo de un vector
3. Vector unitario
4. Propiedades del módulo
5. 7 problemas resueltos

Otros temas de vectores de \(\mathbb{R}^2\):

• Diferencias entre módulo, dirección y ángulo de un vector
• Sumar y restar vectores del plano real
• Vector que une dos puntos del plano
• Producto de un escalar por un vector del plano real
• Producto escalar de dos vectores del plano
• Vectores del plano real (resumen)

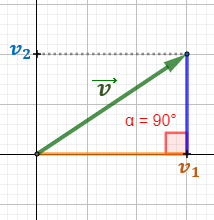
Recordad que la primera coordenada de un vector \(\vec{v} = (v_1,v_2)\) es \(v_1\) y la segunda coordenada es \(v_2\).

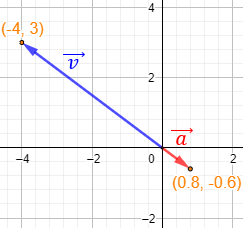
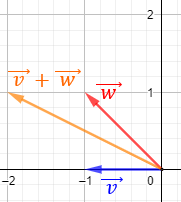
El vector \(\vec{v}\) se representa en el plano como una flecha que parte del origen (punto \((0,0)\)) y termina en el punto con las coordenadas del vector, \(P=(v_1,v_2)\):

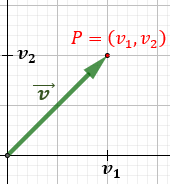
No obstante, podemos representar el vector \(\vec{v}\) en cualquier punto del plano porque lo que realmente nos importa es su longitud, su dirección y su sentido.

Sea \(\vec{v}\) el vector dado por

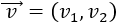
Se define su módulo como

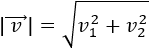
Es decir, el módulo de un vector es la raíz cuadrada (positiva) de la suma de los cuadrados de sus coordenadas.

Un vector \(\vec{v}\) es unitario cuando su módulo es 1:

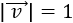
Es decir, el vector \(\vec{v}\) es unitario cuando su longitud es 1.

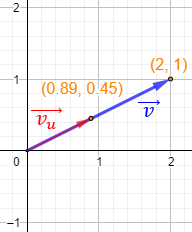
Si dividimos el módulo de un vector \(\vec{v}\) entre su módulo, obtenemos un vector unitario que tiene la misma dirección y el mismo sentido que \(\vec{v}\). Normalmente, a este vector se le denota por \(\vec{v_u}\) y se le denomina vector unitario de \(\vec{v}\). Ver el Problema 3.

---

Las propiedades básicas del módulo son las siguientes:

• El módulo de un vector \(\vec{v}\) es siempre mayor o igual que 0, siendo 0 sólo cuando \(\vec{v} = (0,0)\).
• Si \(\lambda\) es un número real y \(\vec{v}\) es un vector, entonces

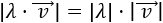
• Dados dos vectores \(\vec{v}\) y \(\vec{w}\), el módulo de su suma cumple

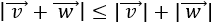
Las demostraciones se encuentran en los problemas 13, 14 y 15 de la página Vectores del plano.

Problema 1

Calcular el módulo de los siguientes 5 vectores y determinar si alguno de ellos es unitario:

Problema 2

Comprobar que los siguientes 4 vectores tienen el mismo módulo, pero representarlos para determinar cuáles tienen la misma dirección:

Problema 3

Calcular un vector que tenga la misma dirección y el mismo sentido que el vector \(\vec{v}\), y que, además, sea unitario:

Problema 4

Calcular un vector que tenga la misma dirección y sentido contario que el vector \(\vec{v}\), pero que sea unitario:

Representar ambos vectores.

Problema 5

El módulo de la suma de dos vectores no es la suma de los módulos de los vectores. Comprobarlo calculando los módulos de los vectores \(\vec{v}\) , \(\vec{w}\) y \(\vec{v}+\vec{w}\):

Representar los tres vectores.

Problema 6

Calcular el módulo del vector \(\vec{v}\) y el módulo del producto del escalar \(\lambda = -1/3\) por el vector \(\vec{v}=(6,-3)\) para comprobar que se cumple la propiedad siguiente del módulo:

Problema 7

Demostrar que el módulo del vector unitario de un vector es 1, es decir,

---