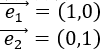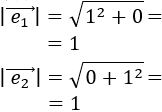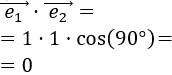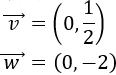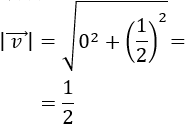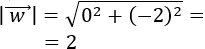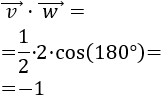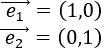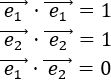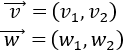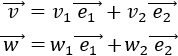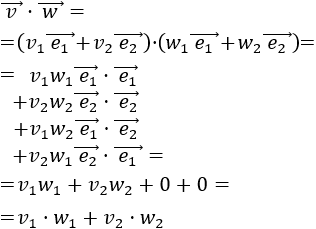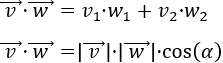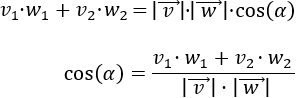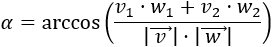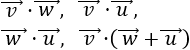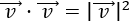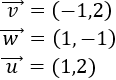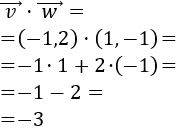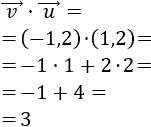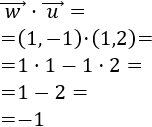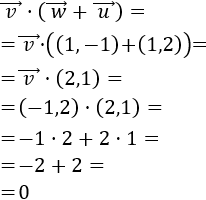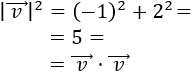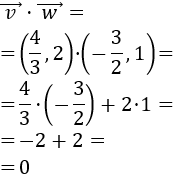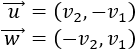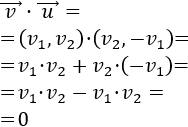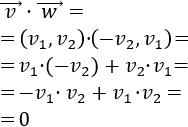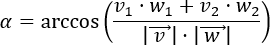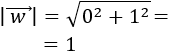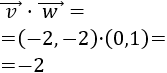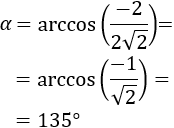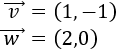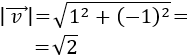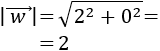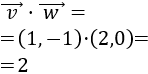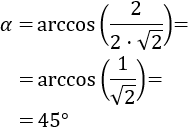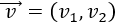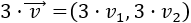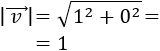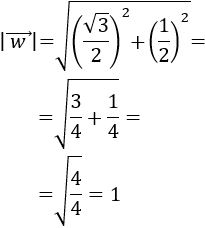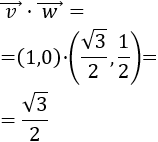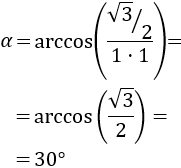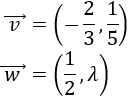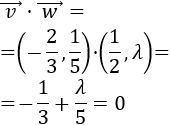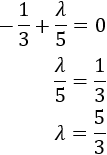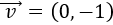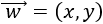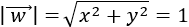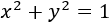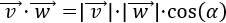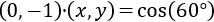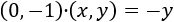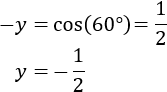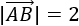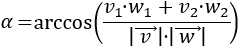Producto escalar de vectores de \(\mathbb{R}^2\)
En está pagina definimos el producto escalar de dos vectores del plano real, \(\mathbb{R}^2\), enumeramos sus propiedades y resolvemos problemas relacionados. Como aplicación, también definimos y calculamos el ángulo que forman dos vectores.
Contenido de esta página:
- Introducción
- Definición 1 del producto escalar
- Propiedades del producto escalar
- Definición 2 del producto escalar
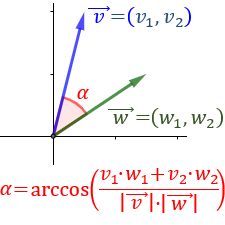
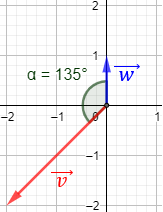
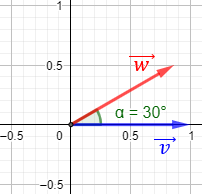
- Ángulo entre dos vectores
- 10 problemas resueltos
Otros temas de vectores de \(\mathbb{R}^2\):
Páginas relacionadas
Páginas amigas:
1. Introducción
Recordamos algunos conceptos necesarios:
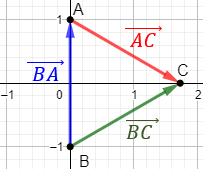
Un vector del plano \(\mathbb{R}^2\) es \(\vec{v} = (v_1, v_2)\), siendo \(v_1\) y \(v_2\) números reales, llamados primera y segunda coordenada de \(\vec{v}\).
Dado un escalar \(\alpha\) (un número real), el producto \(\alpha ·\vec{v}\) se calcula multiplicando las coordenadas del vector \(\vec{v}\) por \(\alpha\):
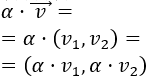
El módulo del vector \(\vec{v} = (v_1, v_2)\) es la raíz cuadrada de la suma de los cuadrados de sus coordenadas:
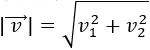
Hay dos formas de calcular el producto escalar de dos vectores y debemos conocer ambas.
2. Definición 1 del producto escalar
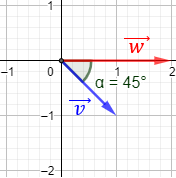
Sean los vectores del plano \(\vec{v}\) y \(\vec{w}\), se define su producto escalar como
$$ \vec{v}·\vec{w} = |v|·|w|·cos(\alpha) $$
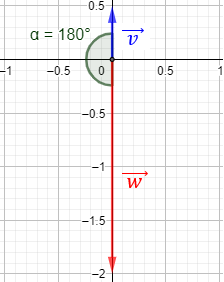
donde \(\alpha\) es el ángulo que forman los vectores \(\vec{v}\) y \(\vec{w}\) entre sí, comprendido en el intervalo \(\left[0, \pi \right]\).
Es decir, el producto vectorial de \(\vec{v}\) y \(\vec{w}\) es el producto de sus módulos por el coseno del ángulo que forman.
Recordad que un escalar es cualquier número real \(k\) de \(\mathbb{R}\).
El producto escalar de dos vectores se denomina escalar porque su resultado es un número real.
3. Propiedades del producto escalar
-
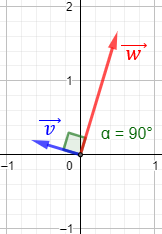
Si uno de los dos vectores \(\vec{v}\) ó \(\vec{w}\) es 0, su producto escalar es 0. El recíproco no es cierto: el producto puede ser 0 sin que ninguno de los vectores sea 0 (como en el ejemplo 1).
-
El producto escalar es conmutativo, es decir,
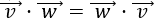
-
El producto escalar es distributivo respecto de la suma de vectores:
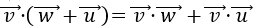
-
Extracción de un escalar \(\lambda\in\mathbb{R}\):
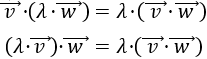
-
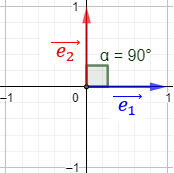
Si los vectores \(\vec{v}\) y \(\vec{w}\) son ortogonales (perpendiculares), entonces su producto escalar es 0.
-
El producto de un vector por sí mismo es el cuadrado de su módulo:
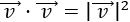
-
El módulo de un vector es igual a la raíz cuadrada de su cuadrado:
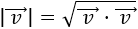
4. Definición 2 del producto escalar
El producto escalar de los vectores \( \vec{v} = (v_1, v_2)\) y \(\vec{w} = (w_1, w_2)\) es
$$\vec{v} ·\vec{w} = v_1·w_1 + v_2·w_2 $$
La definición 1 y la definición 2 son equivalentes (el resultado del producto es el mismo).