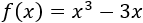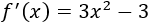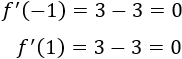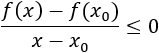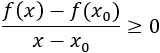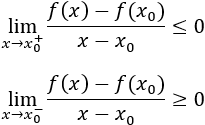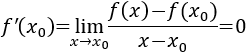Derivada 0 en los extremos relativos

En esta página demostramos que la derivada nula en un punto es una condición necesaria para ser un extremo relativo.

Contenido de esta página:

1. Enunciado
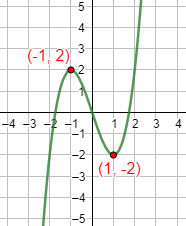
2. Ejemplo
3. Demostración

Enlace: problemas de máximos y mínimos.

Sea la función de variable real \(f:]a,b[\to \mathbb{R}\) derivable en el punto \(x_0 \in ]a,b[\).

Recordatorio de extremo relativo:

• El punto \(x_0\) es un mínimo relativo si existe \(\varepsilon >0\) tal que \(f(x_0) \leq f(x)\) para todo \(x\in ]x_0-\varepsilon , x_0+\varepsilon [\).
• El punto \(x_0\) es un máximo relativo si existe \(\varepsilon >0\) tal que \(f(x_0) \geq f(x)\) para todo \(x\in ]x_0-\varepsilon , x_0+\varepsilon [\).

Sea la función

Su gráfica es

Podemos ver en su gráfica que tiene un máximo en \(x=-1\) y un mínimo en \(x=1\).

La derivada de la función es

Comprobamos que se anula en los extremos vistos:

La aplicación de este resultado es obvia: los puntos que anulan la primera derivada (llamados puntos críticos) son posibles extremos relativos de la función.

Para asegurar si un punto crítico es un extremo, podemos aplicar los criterios de la primera o segunda derivada.

Supongamos que \(x_0\) es un máximo local (si es un mínimo, la demostración es análoga).

Por la definición de máximo local, existe un intervalo \( ]x_0-\varepsilon , x_0+\varepsilon [\) entorno de \(x_0\) donde \(f(x) \leq f(x_0)\) para todo \(x\) del entorno.

Para \(x \in ]x_0, x_0+\varepsilon [\) se tiene

Para \(x \in ]x_0-\varepsilon , x_0 [\) se tiene

Como consecuencia, los límites laterales de la definición de derivada en \(x_0\) son

Pero como la función es derivable en el punto \(x_0\), los límites anteriores existen y coinciden, por lo que

---

---