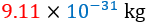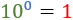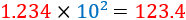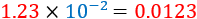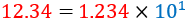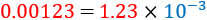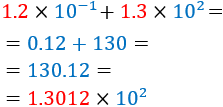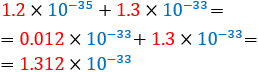Pregunta 0 (introductoria) 
Al multiplicar un número decimal por una potencia de 10,
la coma decimal (o punto decimal) se desplaza...
|
|
Hacia la derecha si el exponente es negativo y hacia la izquierda si el exponente es positivo.
|
|
|
Hacia la derecha si el exponente es positivo y hacia la izquierda si el exponente es negativo.
|
Pregunta 1 
El número 347.1 puede escribirse en notación científica como...
|
|
$$ 3471 \times 10^{-2}$$
|
|
|
$$ 3.471 \times 10^{2}$$
|
|
|
$$ 3471 \times 10^{-1}$$
|
Pregunta 2 
El número 0.0005 en notación científica es...
|
|
$$ 5\cdot 10^{3}$$
|
|
|
$$ 5 \cdot 10^{-3}$$
|
|
|
$$ 5 \cdot 10^{-4}$$
|
Pregunta 3 
El número 0,3232 en notación científica es...
|
|
$$ 3.232\cdot 10^{3}$$
|
|
|
$$ 3\text{,}232 \cdot 10^{-1}$$
|
|
|
$$ 3\text{,}232 \times 10^{-2}$$
|
Pregunta 4 
El número \(5.9\times 10^{-2}\) es el número decimal...
|
|
$$ 0\text{,}0059$$
|
|
|
$$ 0\text{,}059 $$
|
|
|
$$ 590 $$
|
Pregunta 5 
El número \(0.174\times 10^2\)...
|
|
Tiene mantisa 0.174 y orden de magnitud 102.
|
|
|
Tiene mantisa 102 y orden de magnitud 0.174.
|
|
|
No está escrito correctamente en notación científica.
|
Pregunta 6 
El número 0,111·10-2 ...
|
|
Está escrito en notación científica.
|
|
|
Es el número decimal 0.00111.
|
|
|
En notación científica es el número \(1.11\times 10^{-4}\).
|
Pregunta 7 
El número 36,003 escrito en notación científica es...
|
|
$$ 36003\cdot 10^{-3}$$
|
|
|
$$ 3.6003 \cdot 10$$
|
|
|
$$ 360\text{,}03 \times 10^{-1}$$
|
Pregunta 8 
El número \(58.013\times 10^{-4}\)...
|
|
Está escrito correctamente en notación científica.
|
|
|
En notación científica es \(5.8013 \times 10^{-5}\).
|
|
|
Es el número decimal 0.0058013.
|
Pregunta 9 
El número decimal 3.0002 en notación científica es...
|
|
$$ 30\text{,}002\times 10^{-1}$$
|
|
|
$$ 3.0002 \times 10^0$$
|
|
|
$$ 3\text{,}0002 \times 10^1$$
|
Pregunta 10 
El número \(7.012\cdot 10^2\)...
|
|
Está escrito correctamente en notación científica.
|
|
|
Es el número decimal 0.07012.
|
|
|
Es el número decimal 7012.
|
Pregunta 11 
El número \(0.0101\cdot 10^{-2}\)...
|
|
No está escrito correctamente en notación científica y es el número decimal 0,000101.
|
|
|
En notación científica es el número \(1.01 \times 10^{-2}\).
|
|
|
No puede escribirse en notación científica.
|
Pregunta 12 
El número 3000·10-3 ...
|
|
Es el número 3.
|
|
|
Está escrito en notación científica.
|
|
|
No puede escribirse en notación científica.
|
Pregunta 13 
El número 11,11·103 ...
|
|
Es el número 1111000.
|
|
|
Es el número 1111,00.
|
|
|
En notación científica es \(1.111 \times 10^{4}\).
|
Pregunta 14 
El número 0.0001203 en notación científica es...
|
|
$$ 0.1203\times 10^{-3}$$
|
|
|
$$ 1.203\times 10^{3}$$
|
|
|
$$ 1.203\times 10^{-4}$$
|
Pregunta 15 
El número 1,3010·103 ...
|
|
Es el número decimal 13010.
|
|
|
En notación científica es el número \(1.301\times 10^{3}\).
|
|
|
En notación científica es el número \(1.301\times 10^{-3}\).
|
Pregunta 16 
El número 0.000093 en notación científica es...
|
|
$$ 0.93\times 10^{-4}$$
|
|
|
$$ 93\text{,}00 \cdot 10^{-6}$$
|
|
|
$$ 9.3\times 10^{-5}$$
|
Pregunta 17 
El número \(1.23\times 10^{2}\)...
|
|
Es el número natural 123.
|
|
|
Es el número decimal 0.00123.
|
|
|
No está escrito correctamente en notación científica.
|
Pregunta 18 
Si la masa del electrón es \(9.11\times 10^{-31}\) kg y la masa del protón es \(1.67\times 10^{-27}\) kg, entonces...
|
|
El electrón tiene más masa que el protón.
|
|
|
El electrón tiene menos masa que el protón.
|
|
|
No se pueden comparar las masas porque el orden de magnitud es distinto.
|
Pregunta 19 
Si el orden de magnitud de un número escrito en notación científica es 10 elevado a un número negativo, entonces...
|
|
Se trata de un número menor que 1.
|
|
|
Puede ser un número menor o mayor que 1 porque depende de la mantisa.
|
|
|
Es un número negativo.
|
Pregunta 20 
El número negativo -0.00078...
|
|
En notación científica es \(-7.8\times 10^{-4}\).
|
|
|
En notación científica es \(7.8\times 10^{-4}\).
|
|
|
No se puede escribir en notación científica porque es negativo.
|