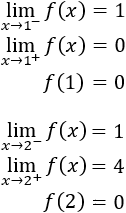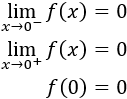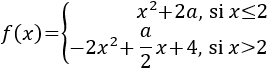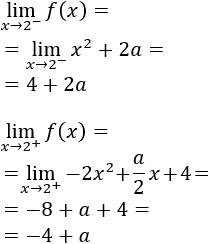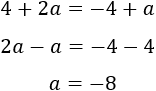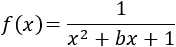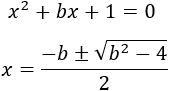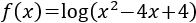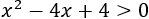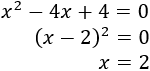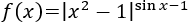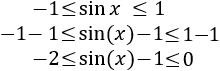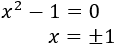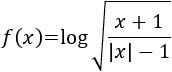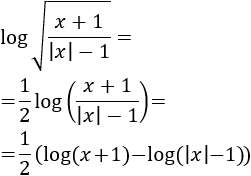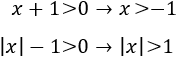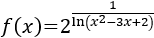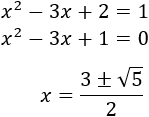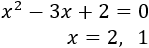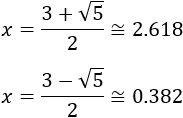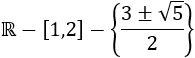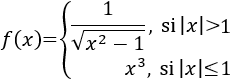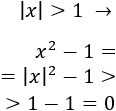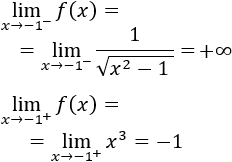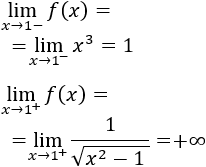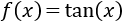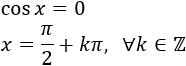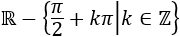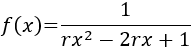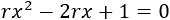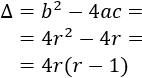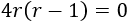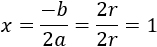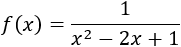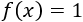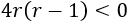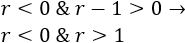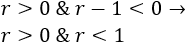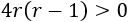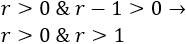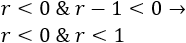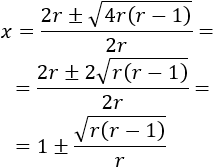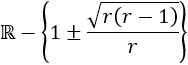Estudiar la continuidad de las siguientes funciones \(f:\mathbb{R}\to\mathbb{R}\).
Ejercicio 1
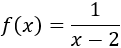
Solución
Como es una función racional, el dominio es el conjunto de los reales excepto los valores para los que se anula en denominador (no se puede dividir entre 0), es decir, el dominio es \(\mathbb{R}-{2}\):
$$ Dom(f) = \mathbb{R}- \{2\} $$
La función es continua en todo su dominio.
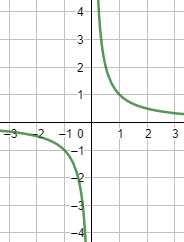
Gráfica:
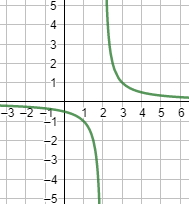
Observad que la función crece (o decrece) indefinidamente cuando \(x\) se acerca a 2 por su derecha (o su izquierda):
$$ \lim_{x \to 2^-} f(x) = -\infty $$
$$ \lim_{x \to 2^+} f(x) = +\infty $$
Esto es debido a que cada vez el denominador es más pequeño y, por tanto, el cociente es cada vez mayor (o menor, si el denominador tiene signo negativo).
Ejercicio 2
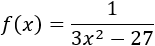
Solución
Como es una función racional, el dominio es el conjunto de los reales excepto donde se anula el denominador. Para hallar estos puntos, igualamos el denominador a 0 y resolvemos la ecuación:
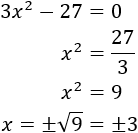
Por tanto, el dominio es el conjunto de los reales excepto \(-3\) y \(3\):
$$ Dom(f) = \mathbb{R}- \{-3,3\} $$
La función es continua en todo su dominio.
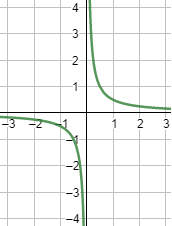
Gráfica:
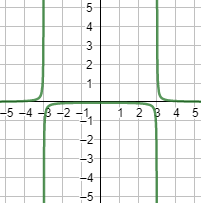
Cuando \(x\)
se aproxima a los puntos de discontinuidad, la función crece/decrece indefinidamente:
$$ \lim_{x \to -3^-} f(x) = +\infty $$
$$ \lim_{x \to -3^+} f(x) = -\infty $$
$$ \lim_{x \to 3^-} f(x) = -\infty $$
$$ \lim_{x \to 3^+} f(x) = +\infty $$
Ejercicio 3
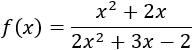
Solución
Lo primero que tenemos que hacer es simplificar la expresión de la función. Para ello, factorizamos los polinomios del numerador y del denominador.
Numerador:
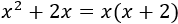
Denominador:
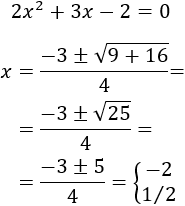
Por tanto,
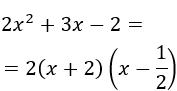
Con lo que podemos escribir la función como
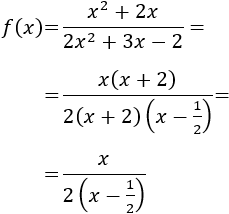
Esto nos permite simplificar la expresión de la función y, podemos observar que, de este modo,
para \(x = -2\) el denominador no se anula.
El dominio es el conjunto de los reales excepto 1/2:
$$ Dom(f) = \mathbb{R}- \{1/2\} $$
La función es continua en todo su dominio por ser racional.
Gráfica:
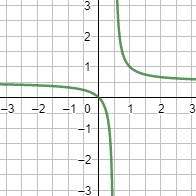
Ejercicio 4
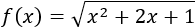
Solución
Como la raíz es cuadrada, hay que asegurarse de que el radicando es no negativo.
Podemos factorizar el radicando:
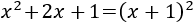
Como un cuadrado es siempre no negativo, el radicando no es negativo, así que el dominio es el conjunto de los reales:
$$ Dom(f) = \mathbb{R} $$
Además, podemos simplificar la función:
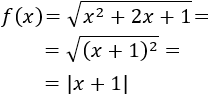
Nota: no debemos olvidar el valor absoluto al cancelar una raíz cuadrada con
un cuadrado.
La función es continua en todo su dominio.
Gráfica:
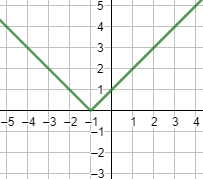
El ángulo que aparece en \(x = -1\) es debido al cambio del signo del argumento del valor absoluto.
Escribimos la función como una función a trozos:
$$ f(x) =
\begin{cases}
x+1 & \quad \text{si } x \geq -1\\
-x-1 & \quad \text{si } x < -1\\
\end{cases} $$
El ángulo es donde conectan ambas rectas de la función.
Ejercicio 5
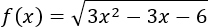
Solución
Como tenemos una raíz cuadrada, hay que asegurarse de que el radicando sea no negativo.
Resolvemos la ecuación de segundo grado:
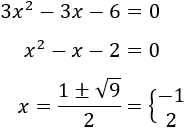
Las soluciones nos proporcionan 3 intervalos donde el signo del radicando se mantiene constante:
![intervalos ]-∞ -1[, ]-1,2[ y ]2,+∞[ Explicamos el concepto de continuidad de una función (especialmente en el caso de las funciones continuas, por lo que usamos límites laterales). Proporcionamos ejemplos y resolvemos ejercicios de calcular el dominio y la continuidad. Ejercicios resueltos. Matemáticas. Bachillerato. Análisis.](https://www.matesfacil.com/BAC/continuidad/conti5-2b.png)
Como el signo no cambia en los intervalos, podemos dar un valor cualquiera a \(x\) para determinar el signo en cada intervalo:
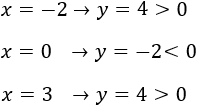
En el intervalo \(]-1,2[\), el radicando es negativo.
Nota: En realidad, como se trata de una parábola cuyo vértice es un mínimo, podemos deducir directamente que sólo es negativa en el intervalo central.
Por tanto, el dominio es el conjunto de los reales menos el intervalo \(]-1,2[\):
$$ Dom(f) = \mathbb{R}-]-1,2[ $$
O bien,
$$ Dom(f) = ]-\infty,-1[\cup [2,+\infty[ $$
La función es continua en su dominio.
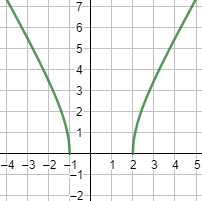
Gráfica:
Ejercicio 6
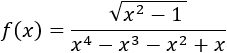
Solución
-
El radicando de la raíz debe ser no negativo.
-
El denominador tiene que ser distinto de 0.
Igualamos el radicando a 0:
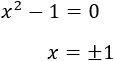
Hay que estudiar el signo del radicando los intervalos siguientes:
![intervalos ]-∞-1[, ]-1,1[ y ]1,+∞[ Explicamos el concepto de continuidad de una función (especialmente en el caso de las funciones continuas, por lo que usamos límites laterales). Proporcionamos ejemplos y resolvemos ejercicios de calcular el dominio y la continuidad. Ejercicios resueltos. Matemáticas. Bachillerato. Análisis.](https://www.matesfacil.com/BAC/continuidad/conti6-2b.png)
Dando valores, el radicando es no negativo en el primer y tercer intervalo.
Factorizamos el denominador:
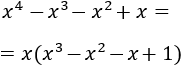
Aplicamos Ruffini para hallar las soluciones del polinomio de tercer grado:
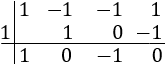
Por tanto,
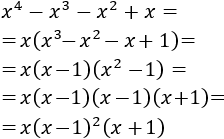
Tenemos que excluir los puntos 0, 1 y -1.
El dominio es
$$ Dom(f) = \mathbb{R}-[-1,1] $$
La función es continua en su dominio.
Gráfica:
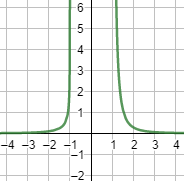
Ejercicio 7
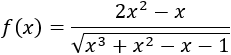
Solución
El radicando tiene que ser positivo (no puede ser 0 porque está en el denominador).
Igualamos a 0 el radicando:
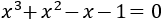
Aplicamos Ruffini para obtener las raíces de la ecuación de tercer grado:
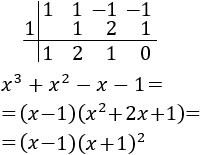
Estudiamos el signo en los siguientes tres intervalos que definen las raíces:
![intervalos ]-∞-1[, ]-1,1[ y ]1,+∞[. Si x=-2, y=-4; si x=0, y=-1; si x=2, y=9 Explicamos el concepto de continuidad de una función (especialmente en el caso de las funciones continuas, por lo que usamos límites laterales). Proporcionamos ejemplos y resolvemos ejercicios de calcular el dominio y la continuidad. Ejercicios resueltos. Matemáticas. Bachillerato. Análisis.](https://www.matesfacil.com/BAC/continuidad/conti7-3b.png)
Por tanto, el dominio es
$$ Dom(f) = ]1,+\infty [ $$
Nota: no incluimos el extremo para que no se anule el denominador.
La función es continua en su dominio.
Gráfica:
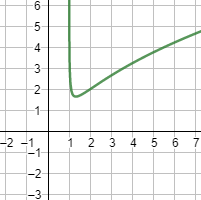
Ejercicio 8
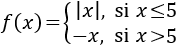
Solución
El dominio es todos los reales.
Podemos reescribir la función como
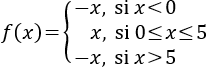
Tenemos que estudiar la continuidad en los puntos donde cambia la definición.
Límites laterales en 0:
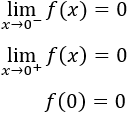
La función es continua en \(x=0\).
Límites laterales en 5:
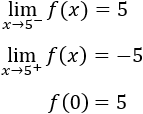
Como no coinciden, la función no es continua en \(x=5\).
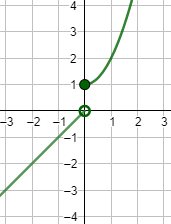
Gráfica:
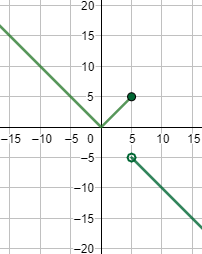
Ejercicio 9
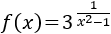
Solución
El dominio es el conjunto de los reales excepto aquellos puntos que anulan el denominador del exponente, que son 1 y -1:
$$ Dom(f) = \mathbb{R}-\{-1,1\} $$
Podemos considerar la función como una raíz cuyo radicando (la base de la potencia) es siempre positivo. Por tanto, la función es continua en su dominio.
Gráfica:
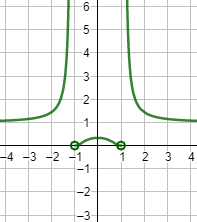
Ejercicio 10
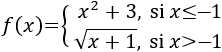
Solución
Observad que el radicando es positivo si \(x>-1\), así que el dominio es el conjunto de los reales.
- Si \(x < -1\), la función es continua por ser polinómica.
- Si \(x > -1\), la función es continua por ser una raíz cuadrada con radicando positivo.
Tenemos que estudiar la continuidad en -1.
Calculamos los límites laterales en dicho punto:
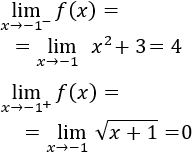
Como los límites laterales no coinciden, no existe el límite de la función en dicho punto:
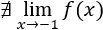
Luego la función es continua en \(\mathbb{R}-\{-1\}\).
Gráfica:
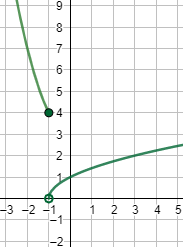
Ejercicio 11
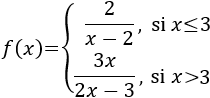
Solución
-
En el intervalo \(x\leq 3\), la función es racional. Tenemos que excluir \(x=2\) porque anula al denominador.
-
En el intervalo \(x> 3\), también es racional.El denominador se anula en \(x = 3/2 < 3\), así que no hay que excluir ningún punto.
El dominio de la función es \(\mathbb{R}-\{2\}\).
Tenemos que estudiar la continuidad en el punto \(x=3\).
Calculamos los límites laterales
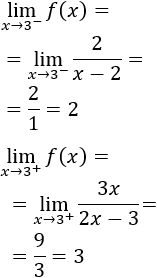
Como no coinciden, la función no es continua en \(x=3\).
La función es continua en \(\mathbb{R}-\{2,3\}\).
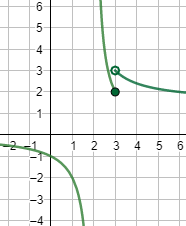
Gráfica:
Ejercicio 12
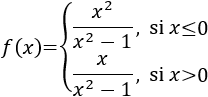
Solución
Los denominadores se anulan cuando \(x =\pm 1\). El negativo anula el denominador de la primera fracción y el positivo anula el de la segunda. Por tanto, el dominio es
$$ Dom(f) = \mathbb{R}-\{-1,1\} $$
Calculamos los límites laterales en \(x=0\):
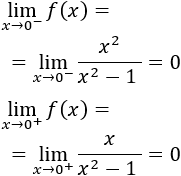
Los límites coinciden y, además, coinciden con \(f(0)\).
Por tanto, la función es continua en \(\mathbb{R}-\{-1,1\}\).
Gráfica:
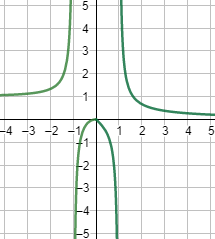
Ejercicio 13
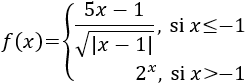
Solución
En el intervalo \(x< -1\), la función es continua: el radicando es positivo y, por tanto, el denominador no se anula.
En el intervalo \(x>-1\), la función es continua por ser una exponencial.
El dominio es el conjunto de los reales.
Hay que estudiar la continuidad en el punto \(x=-1\).
Calculamos límites laterales:
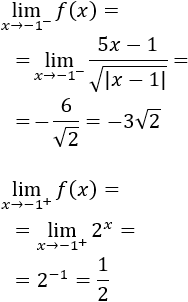
Como los límites no coinciden, la función no es continua en \(x=-1\).
La función es continua en \(\mathbb{R}-\{-1\}\).
Gráfica:
Ejercicio 14
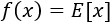
Solución
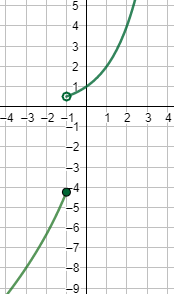
La función \(f(x) = E[x]\) es la parte entera de \(x\)
:
- Si \(x
> 0\) , es el número a la izquierda de la coma decimal y,
- si \(x
< 0\), es el número a la izquierda de la coma decimal restándole 1.
Por ejemplo,
![E[3.1]=3 , E[2.1]=2, E[-0.21]=-1 y E[-3.5]=-4 Explicamos el concepto de continuidad de una función (especialmente en el caso de las funciones continuas, por lo que usamos límites laterales). Proporcionamos ejemplos y resolvemos ejercicios de calcular el dominio y la continuidad. Ejercicios resueltos. Matemáticas. Bachillerato. Análisis.](https://www.matesfacil.com/BAC/continuidad/conti14-1b.png)
El dominio de la función es todos los reales.
La función es constante en los intervalos de longitud 1 con extremos enteros. En los positivos:
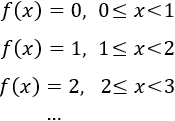
En los negativos:
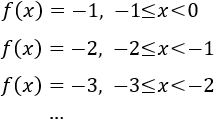
En cada uno de los intervalos (considerándolos abiertos), la función es continua por ser constante.
No es necesario que calculemos los límites laterales en cada extremo de los intervalos, ya que es evidente que estos nunca van a coincidir.
La función es, pues, continua en todos los reales excepto en los enteros, es decir, es continua en \(\mathbb{R}-\mathbb{Z}\).
Gráfica:
Ejercicio 15
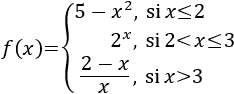
Solución
El dominio es todos los reales.
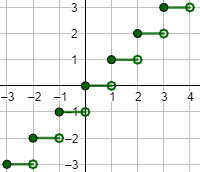
En cada intervalo (abierto) de definición, la función es continua. Tenemos que ver qué ocurre en los puntos \(x=2\) y \(x=3\).
Límites laterales en 2:
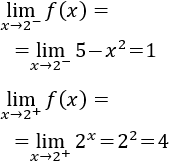
Como los límites son distintos, no hay continuidad en \(x
= 2\).
Límites laterales en 3:
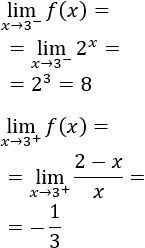
Como los límites son distintos, no hay continuidad en \(x
= 3\).
Por tanto, la función es continua en el conjunto \(\mathbb{R}-\{2,3\}\).
Gráfica:
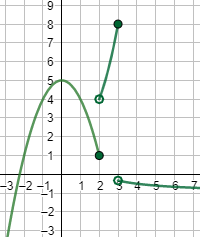
Ejercicio 16 (dificultad alta)
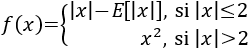
Solución
En el ejercicio 14 ya vimos cómo funciona la función parte entera, \(E[x]\).
El dominio es todos los reales.
Observad que para \(|x|\leq 2\),
![f(-x) = |-x| -E[|x|] = f(x) Explicamos el concepto de continuidad de una función (especialmente en el caso de las funciones continuas, por lo que usamos límites laterales). Proporcionamos ejemplos y resolvemos ejercicios de calcular el dominio y la continuidad. Ejercicios resueltos. Matemáticas. Bachillerato. Análisis.](https://www.matesfacil.com/BAC/continuidad/P16-1.png)
Y para \(|x|> 2\),
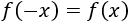
Esto significa que hay simetría respecto del eje de ordenadas y como consecuencia, si \(f\) es continua en un punto \(a\), también es continua en \(-a\).
Estudiaremos la continuidad en los positivos (y en 0) y sabremos también la continuidad en los negativos.
a) Intervalo \(0< x \leq 2\)
En los enteros, la función es 0:
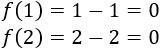
En los decimales,
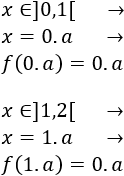
Es decir,
![f(x)=x si x está en ]0,1[, f(x)=0 si x=1, f(x)=x-1 si x está en ]1,2[ y f(x)=0 si x=2 Explicamos el concepto de continuidad de una función (especialmente en el caso de las funciones continuas, por lo que usamos límites laterales). Proporcionamos ejemplos y resolvemos ejercicios de calcular el dominio y la continuidad. Ejercicios resueltos. Matemáticas. Bachillerato. Análisis.](https://www.matesfacil.com/BAC/continuidad/P16-5.png)
La función no es continua en \(x=1\) ni en \(x=2\) ya que los límites laterales no coinciden:
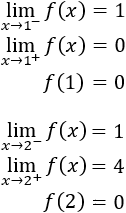
Por la simetría, \(f\) tampoco es continua en \(x=-1\) ni en \(x=-2\).
b) Si \(x=0\), la función es continua:
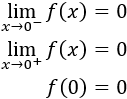
c) Intervalo \(x > 2\)
La función es continua por ser un monomio.
Por la simetría, también lo es en \(x < -2\).
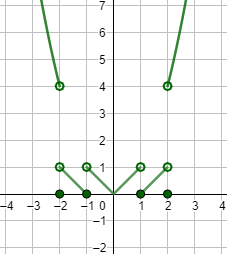
Por tanto, \(f\) es continua en el conjunto
$$ \mathbb{R}-\{-2, -1, 1, 2\} $$
Gráfica:
Ejercicio 17
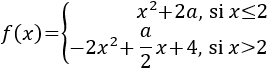
siendo \(a\in\mathbb{R}\) un parámetro.
Solución
La continuidad es clara para \(x\neq 2\) por tratarse de funciones polinómicas, independientemente del valor de \(a\).
Tenemos que estudiar la continuidad en \(x=2\) y ésta dependerá, seguramente, del valor que tome \(a\).
Calculamos los límites laterales en el punto \(x=2\):
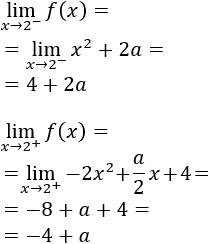
Para que sea continua, los límites deben ser iguales a \(f(2) = 4+2a\). Igualamos:
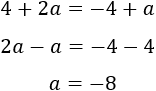
Por tanto,
-
Si \(a=-8\), la función es continua en todo \(\mathbb{R}\).
-
Si \(a\neq -8\), la función es continua en \(\mathbb{R}-\{a\}\).
Gráfica (\(a=-8\)):
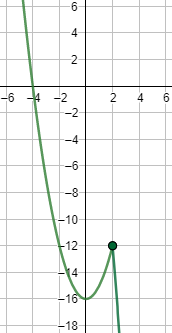
Ejercicio 18 (dificultad alta)
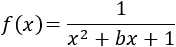
donde \(b\in\mathbb{R}\) es un parámetro.
Solución
Hay que excluir del dominio las raíces del polinomio del denominador.
Resolvemos la ecuación de segundo grado:
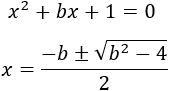
Estudiamos la continuidad según el valor del discriminante:
-
Si \(b^2-4 < 0\), la ecuación no tiene soluciones reales y la función es continua.
Esto ocurre cuando \(|b|<2\).
-
Si \(b^2-4 = 0\), la ecuación tiene única solución: \(x = -b/2\). Esto ocurre cuando \(b=\pm 2\). En este caso, la función no es continua en \(x =1\) ó \(x = -1\).
-
Si \(b^2-4 > 0\), la ecuación tiene dos soluciones. Esto ocurre cuando \(|b|>2\). La función es discontinua en las raíces.
Resumiendo,
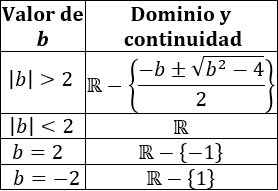
Gráfica (\( b =2.1\)):
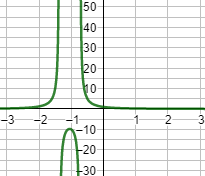
Gráfica (\( b =-1.9\)):
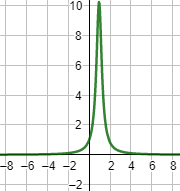
Gráfica (\( b =2\)):
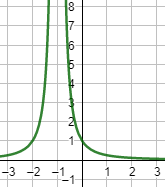
Gráfica (\( b =-2\)):
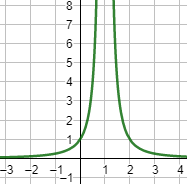
Ejercicio 19
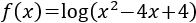
Solución
Como es una función logarítmica, su argumento (lo de dentro del logaritmo) debe ser positivo.
Por tanto, debemos excluir del dominio las soluciones de la inecuación
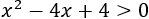
Resolvemos la ecuación de segundo grado asociada:
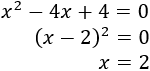
Tenemos que estudiar el signo en los intervalos \((-\infty ,2)\) y \((2,+\infty)\).
En ambos intervalos el polinomio es positivo (se trata de una parábola con vértice sobre el eje de abscisas).
El único punto a excluir del dominio es \(x = 2\).
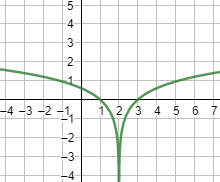
La función es continua en todo su dominio, es decir, en \(\mathbb{R}-\{2\}\).
Gráfica:
Ejercicio 20
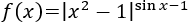
Solución
La función es una potencia con base mayor o igual que 0 (porque es un valor absoluto), así que el único problema que puede surgir es que cuando el exponente sea negativo, la base sea 0.
Estudiamos el signo del exponente:
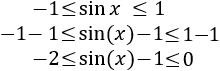
Luego el exponente siempre es menor o igual que 0.
Calculamos los puntos donde se anula la base:
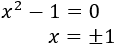
El dominio es todos los reales excepto \(x=\pm 1\):
$$ Dom(f) = \mathbb{R}-\{-1,+1\}$$
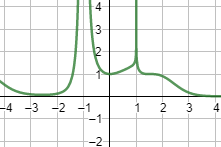
La función es continua en todo su dominio, \(\mathbb{R}-\{-1,+1\}\).
Gráfica:
Ejercicio 21
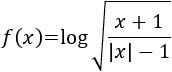
Solución
-
El argumento del logaritmo debe ser positivo.
-
El radicando debe ser no negativo.
-
El denominador debe ser no nulo.
Aplicando las propiedades de los logaritmos,
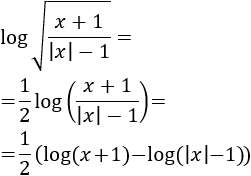
De este modo, es fácil ver que deben cumplirse las siguientes inecuaciones:
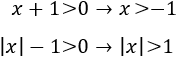
Se cumplen ambas sólo si \(x>1\).
Así, pues, el dominio de la función es \(]1,+\infty [\).
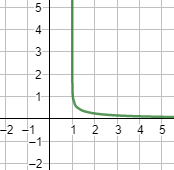
La función es continua en su dominio, \(]1,+\infty [\).
Gráfica:
Ejercicio 22
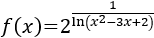
Solución
El denominador del exponente debe ser distinto de 0 y, además, el argumento del logaritmo debe ser positivo.
El denominador se anula cuando el argumento del logaritmo es 1, es decir, cuando
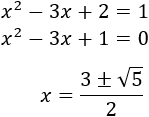
Calculamos las raíces del argumento:
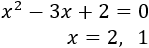
Tenemos que estudiar el signo del polinomio en los intervalos \(]-\infty, 1[\), \(]1,2[\) y \(]2,+\infty[\): es positivo en el primer y tercer intervalo.
Hemos visto que los puntos donde se anula el denominador son:
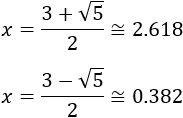
Ambos pertenecen al primer o al tercer intervalo.
Por tanto, el dominio y la coninuidad de la función es
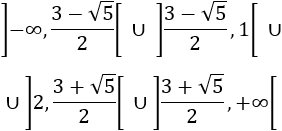
O bien,
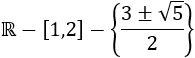
Gráfica:
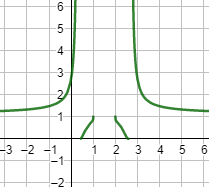
Ejercicio 23
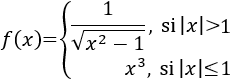
Solución
El radicando siempre es positivo:
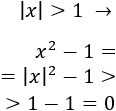
Calculamos los límites laterales en \(x=-1\):
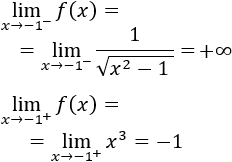
Calculamos los límites laterales en \(x=1\):
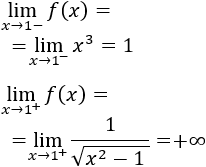
Como los límites laterales no coinciden, la función no es
continua en \(x=-1\) ni en \(x = 1\).
Gráfica:
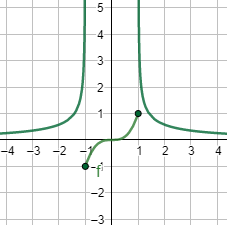
Ejercicio 24
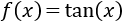
Solución
Podemos escribir la función como un cociente:
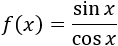
El denominador se anula cuando en infinitos puntos:
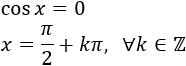
Por tanto, el dominio es
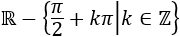
La función es continua en su dominio.
Gráfica:
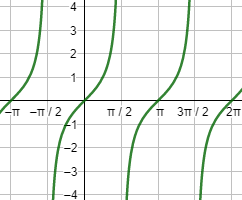
Ejercicio 25
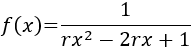
siendo \(r\in\mathbb{R}\) un parámetro.
Solución
Vamos a estudiar la continuidad en función del parámetro \(r\).
Igualamos el denominador a 0:
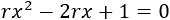
El discriminante de la ecuación es
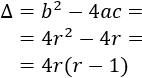
El discriminante nos indica el número de soluciones de la ecuación:
-
Si \(\Delta = 0\), sólo hay una solución.
-
Si \(\Delta < 0\), no hay soluciones.
-
Si \(\Delta > 0\), hay dos soluciones distintas.
Primer caso
Supongamos que \(\Delta = 0\):
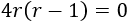
Esto ocurre cuando \(r=0\) ó \(r = 1\).
La solución de la ecuación cuadrática es
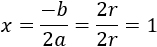
Si \(r = 1\), se trata de la función
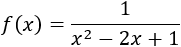
Esta función es continua excepto en \(x = 1\).
Si \(r=0\), se trata de la función constante
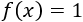
Es una función continua en los reales.
Segundo caso
Supongamos que \(\Delta <0\):
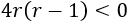
Para ello, debe cumplirse
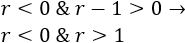
O bien,
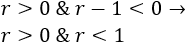
La primera opción es imposible (\(r\) no puede ser negativo y mayor que 1 simultáneamente).
La segunda opción es posible si \(0<r<1\). La función es continua en los reales.
Tercer caso
Supongamos que \(\Delta >0\):
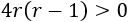
Hay dos opciones:
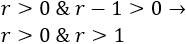
O bien,
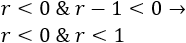
La primera opción es posible si \(r> 1\).
La segunda opción es posible si \(r< 0\).
En ambas opciones, la función es continua en los reales excepto en las dos soluciones de la ecuación cuadrática:
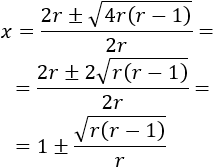
La función es continua en
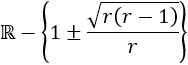
Tabla resumen:

Gráficas (\(0≤ r < 1\)):
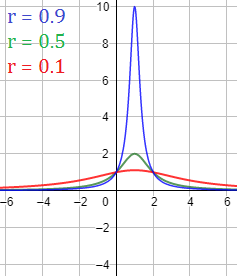
Gráfica (\( r =1\)):
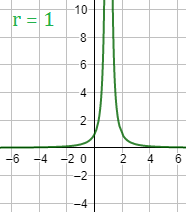
Gráficas (\( r> 1\)):
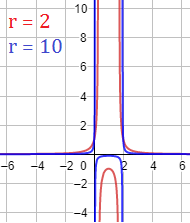
Gráficas (\( r < 0\)):
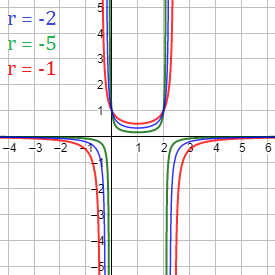


Continuidad de funciones (ejercicios) - © matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.

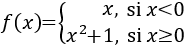
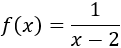

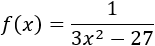
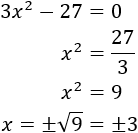

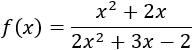
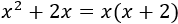
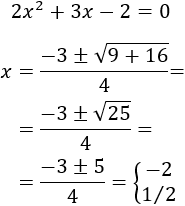
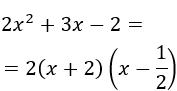
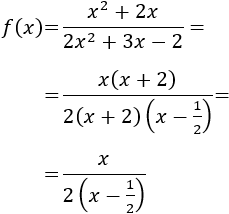

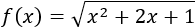
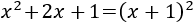
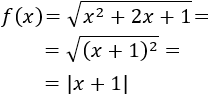

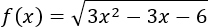
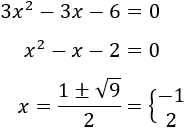
![intervalos ]-∞ -1[, ]-1,2[ y ]2,+∞[ Explicamos el concepto de continuidad de una función (especialmente en el caso de las funciones continuas, por lo que usamos límites laterales). Proporcionamos ejemplos y resolvemos ejercicios de calcular el dominio y la continuidad. Ejercicios resueltos. Matemáticas. Bachillerato. Análisis.](https://www.matesfacil.com/BAC/continuidad/conti5-2b.png)
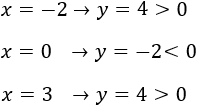

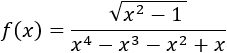
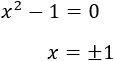
![intervalos ]-∞-1[, ]-1,1[ y ]1,+∞[ Explicamos el concepto de continuidad de una función (especialmente en el caso de las funciones continuas, por lo que usamos límites laterales). Proporcionamos ejemplos y resolvemos ejercicios de calcular el dominio y la continuidad. Ejercicios resueltos. Matemáticas. Bachillerato. Análisis.](https://www.matesfacil.com/BAC/continuidad/conti6-2b.png)
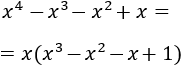
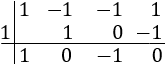
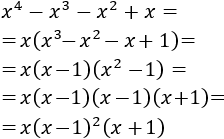

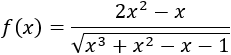
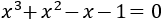
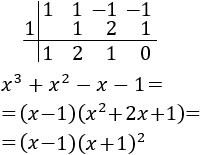
![intervalos ]-∞-1[, ]-1,1[ y ]1,+∞[. Si x=-2, y=-4; si x=0, y=-1; si x=2, y=9 Explicamos el concepto de continuidad de una función (especialmente en el caso de las funciones continuas, por lo que usamos límites laterales). Proporcionamos ejemplos y resolvemos ejercicios de calcular el dominio y la continuidad. Ejercicios resueltos. Matemáticas. Bachillerato. Análisis.](https://www.matesfacil.com/BAC/continuidad/conti7-3b.png)

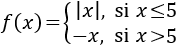
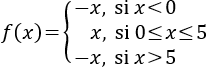
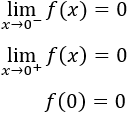
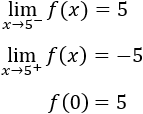

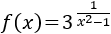

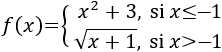
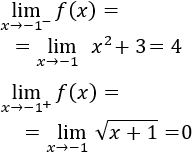
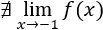

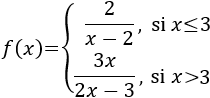
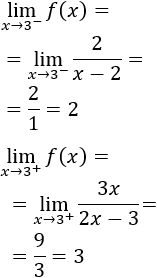

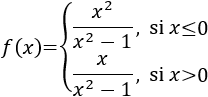
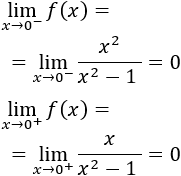

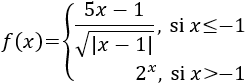
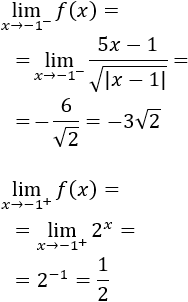

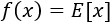
![E[3.1]=3 , E[2.1]=2, E[-0.21]=-1 y E[-3.5]=-4 Explicamos el concepto de continuidad de una función (especialmente en el caso de las funciones continuas, por lo que usamos límites laterales). Proporcionamos ejemplos y resolvemos ejercicios de calcular el dominio y la continuidad. Ejercicios resueltos. Matemáticas. Bachillerato. Análisis.](https://www.matesfacil.com/BAC/continuidad/conti14-1b.png)
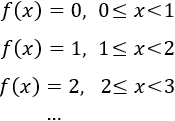
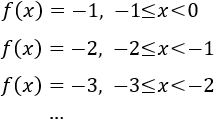

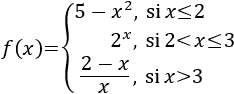
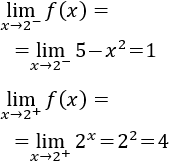
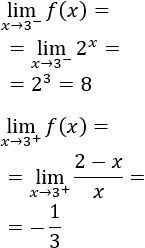

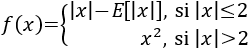
![f(-x) = |-x| -E[|x|] = f(x) Explicamos el concepto de continuidad de una función (especialmente en el caso de las funciones continuas, por lo que usamos límites laterales). Proporcionamos ejemplos y resolvemos ejercicios de calcular el dominio y la continuidad. Ejercicios resueltos. Matemáticas. Bachillerato. Análisis.](https://www.matesfacil.com/BAC/continuidad/P16-1.png)
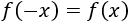
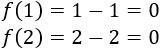
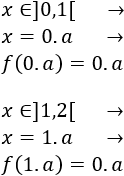
![f(x)=x si x está en ]0,1[, f(x)=0 si x=1, f(x)=x-1 si x está en ]1,2[ y f(x)=0 si x=2 Explicamos el concepto de continuidad de una función (especialmente en el caso de las funciones continuas, por lo que usamos límites laterales). Proporcionamos ejemplos y resolvemos ejercicios de calcular el dominio y la continuidad. Ejercicios resueltos. Matemáticas. Bachillerato. Análisis.](https://www.matesfacil.com/BAC/continuidad/P16-5.png)