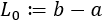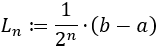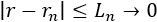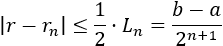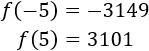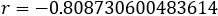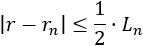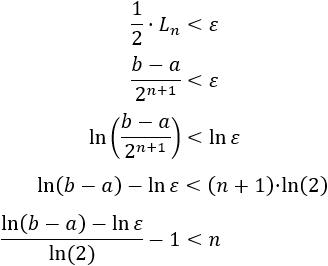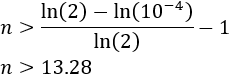Método de bisección
En esta página explicamos el método de bisección, demostramos su convergencia, proporcionamos una cota para el error y resolvemos tres problemas (dos problemas de aplicación y otro más teórico).
Contenido de esta página:
- Introducción
- Método de bisección
- Convergencia y error
- Pseudocódigo
- 3 problemas resueltos
1. Introducción
El método de bisección es un algoritmo de búsqueda de raíces de funciones continuas en un intervalo.
Si una función \(f: \mathbb{R} \rightarrow \mathbb{R} \) es continua en el intervalo \([a,b]\) y cumple que \(f(a)\cdot f(b) < 0\), por el teorema de Bolzano, existe al menos una raíz \(r\) de \(f\) en dicho intervalo (es decir, \(f(r)=0\)).
En el método de bisección, se divide el intervalo \([a,b]\) en dos subintervalos y se escoge el que contiene la raíz para repetir el proceso hasta hallar una aproximación de la misma. Para saber cuál de los dos subintervalos contiene la raíz, se comprueba el signo del producto de las imágenes de sus extremos.
2. Método de bisección
Sea \(f\) una función continua en el intervalo \([a,b]\) tal que \(f(a)·f(b) < 0\).
Definimos las siguientes sucesiones:
-
Sucesión \(\{a_n\}_{n\in\mathbb{N}}\):
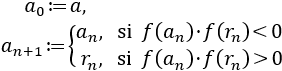
-
Sucesión \(\{b_n\}_{n\in\mathbb{N}}\):
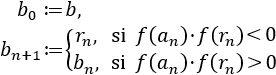
-
Sucesión \(\{r_n\}_{n\in\mathbb{N}}\):
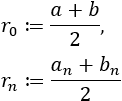
Observad que se cumple \(a_n\leq r_n \leq b_n\).
La aproximación a alguna raíz \(r\) en \([a,b]\) de \(f\) es el valor \(r_n\) (también, podrían servir \(a_n\) y \(b_n\)). Las tres sucesiones convergen a la misma raíz \(r\) de \(f\). Si se escoge \(r_n\) como aproximación, el error cometido es menor o igual que \((b-a)/2^{n+1}\).
Nota 1: definimos \(b_{n+1}\) con las mismas condiciones que \(a_{n+1}\) para tener que hacer sólo una comprobación de signo.
Nota 2: no están definidos los términos \(n+1-\)ésimos si \(f(a_n)·f(r_n) = 0\) porque esto ocurre sólo si \(f(r_n)=0\), con lo que el método habrá hallado la raíz exacta y, por tanto, no se requiere construir más intervalos.
3. Convergencia y error
Bajo las condiciones anteriores, se cumple que las sucesiones convergen a una raíz \(r\) en \([a,b]\) de \(f\):
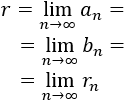
Y, además, una cota para el error es
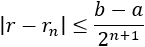
Nota: en el problema 3 se demuestra que el número de iteraciones \(n\) que se precisan para lograr una aproximación \(r_n\) con un error menor que \(\varepsilon\) es
$$ n> \frac{\ln (b-a) -\ln (\varepsilon)}{\ln (2)} - 1 $$
4. Pseudocódigo
A continuación, proporcionamos un pseudocódigo básico del método de bisección. Los argumentos a y b son los extremos del intervalo inicial, max es el número máximo de iteraciones y tol es la cota para el error.
a ← a
b ← b
L ← (b-a)/2 //Longitd del intervalo inicial
N ← 0
Mientras que (L>=tol y N<max)
L ← (b-a)/2 //Longitud del intervalo actual
r ← (a+b)/2 //Punto medio del intervalo actual
Si f(r)=0
Terminar //Porque r es la raíz exacta
Si no,
Si f(a)·f(r)< 0
b ← r //El siguiente intervalo será [a,r]
Si no,
a ← r //El siguiente intervalo será [r,b]
Fin
Fin
N ← N+1
Fin
Mostrar r
5. Problemas resueltos
Problema 1
Aproximar la única raíz real \(r\) de la siguiente función polinómica sabiendo que \(-5\leq r \leq 5\):
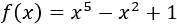
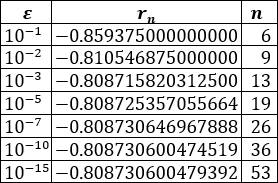
Determinar el número de iteraciones y una cota de error.
Problema 2
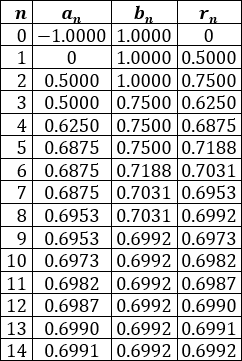
Aproximar la única raíz real \(r\) de la siguiente función polinómica sabiendo que \(-1 \leq r \leq 1\) con una cota de error de \(10^{-4}\):
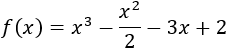
Determinar los extremos \(a_n\) y \(b_n\) de cada intervalo y sus puntos medios \(r_n\).
Problema 3
Dada una cota de error de \(\varepsilon\), deducir una fórmula en función de \(\varepsilon\) y de los extremos del intervalo inicial para determinar el número \(n\) de iteraciones necesarias para hallar la aproximación de la raíz.
Aplicar la fórmula obtenida para la función del problema anterior.
Método de bisección - © matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.