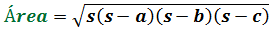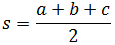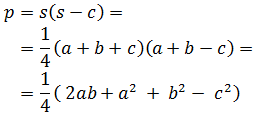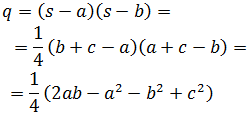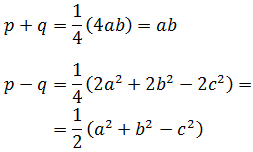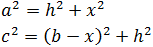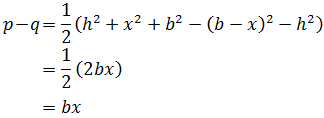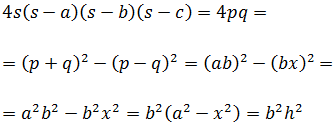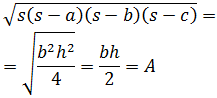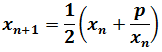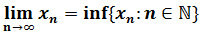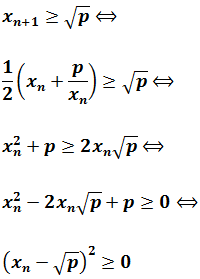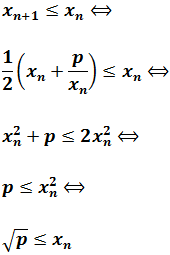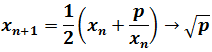Herón de Alejandría

En esta página proporcionamos una breve biografía de Herón de Alejandría y la fórmula de Herón (para calcular áreas de triángulos) y el método de Herón (para la aproximación de raíces cuadradas). Se incluyen ejemplos, demostraciones y un código MatLab del método.

Contenido de esta página:

1. Breve biografía de Herón de Alejandría
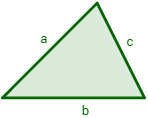
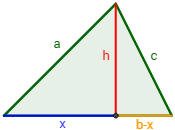
2. Fórmula de Herón (demostración por Pitágoras)
3. Método de Herón (aproximación de la raíz cuadrada):
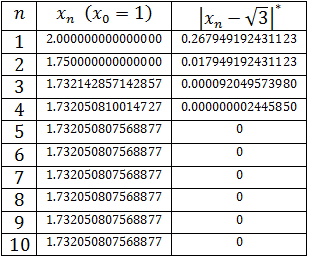
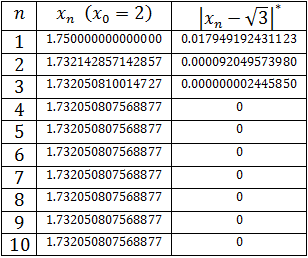
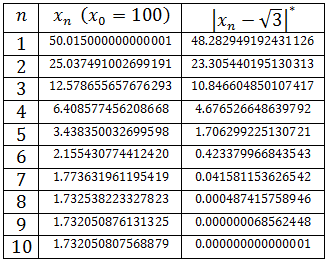
• 3.1. Presentación del método y ejemplos
• 3.2. Demostración de la convergencia

Herón (o Hero) de Alejandría vivió aproximadamente entre los siglos I y II d. C. en Alejandría (norte de Egipto). Fue ingeniero y matemático, inventor de la primera máquina a vapor (conocida por el nombre de Eolípila). Los textos que se le atribuyen tratan sobre todo de mecánica y matemáticas.

En la obra Métrica, compuesta por tres libros, proporciona fórmulas y métodos bastante rigurosos, para calcular áreas de polígonos regulares, triángulos, cuadriláteros y elipses, así como para calcular volúmenes de esferas, cilindros y conos.

Es en el primer libro de Métrica donde presenta la fórmula conocida hoy como la Fórmula de Herón, que veremos a continuación. También mostraremos el Método de Herón para aproximar raíces cuadradas, cuya autoría también se atribuye a Herón. Este método se utiliza todavía en computación.

El área del triángulo de lados a, b y c es

donde s es el semiperímetro de triángulo:

Ejemplo:

Antes de la demostración, veamos un ejemplo de aplicación de la Fórmula. Supongamos que queremos calcular el área del triángulo equilátero de lado 1:

Puesto que el triángulo es equilátero, sus tres lados miden lo mismo: 1.

Por tanto, el semiperímetro es

$$ s = \frac{1+1+1}{2} = \frac{3}{2} $$

Aplicando la Fórmula de Herón, el área es

$$ Área = \sqrt{\frac{1}{2}\cdot \frac{1}{2}\cdot \frac{1}{2}\cdot \frac{3}{2}} = $$

$$ =\frac{1}{2} \cdot \sqrt{\frac{1}{2}\cdot \frac{3}{2}} =$$

$$ =\frac{1}{2} \cdot \sqrt{\frac{3}{4}} =$$

$$ =\frac{1}{4} \cdot \sqrt{3}$$

Demostración:

La siguiente demostracón de la fórmula de Herón es moderna y sólo requiere la aplicación del Teorema de Pitágoras y un poco de cálculo.

Sabemos de antemano que el área del triángulo es

siendo h la altura y b la base.

Para simplificar los cálculos, usaremos la siguiente identidad:

Definimos p y q como

Escribiendo la definición del semiperímetro s, en las expresiones anteriores obtenemos que p es

y q es

Por tanto, la suma y la resta de p y q son:

Consideremos la siguiente descomposición del triángulo en dos triángulos rectángulos:

La base b la hemos dividido en los dos segmentos x y b-x, determinados por la altura h.

Como la altura forma un ángulo recto, aplicando Pitágoras:

Sustituimos en la expresión de p-q:

Entonces, por la identidad que vimos y los cálculos anteriores, sabemos que

(la última igualdad es por Pitágoras).

Por tanto, dividiendo entre 4 y tomando raíces,

Es decir, la fórmula de Herón nos proporciona el área del triángulo de base b y altura h.

El Método de Herón consiste en calcular los términos de la sucesión definida por recurrencia como sigue:

siendo p el número cuya raíz cuadrada queremos aproximar.

El primer término, x₀, debe ser una aproximación a la raíz que buscamos.

3.1. Presentación del método y ejemplos

Se trata de un método que converge muy rápidamente: en unas pocas iteraciones se obtienen aproximaciones con bastantes decimales exactos, incluso cuando se toma como x₀ un número alejado del que se quiere aproximar.

Además, el método es muy simple a la hora de implementar computacionalmente (ver función MatLab).

Veamos un ejemplo: aproximación de la raíz de 3 con diferentes términos iniciales:

$$ \sqrt{3} \simeq 1.732050807568877 $$

Comenzaremos inicialmente con x₀ = 1, x₀ = 2 y x₀ = 100. Realizaremos 10 iteraciones:

Para x₀ = 1:

*Nota: como el error (tercera columna) se ha calculado computacionalmente, el error es 0 cuando se supera la precisión del computador.

Para x₀ = 2:

Para x₀ = 100:

El código utilizado es:

1   function x=raiz(p,a,n)
2   % aproximación de la raíz de p
3   % a es el término x_0
4   % n es el número de iteraciones
5   % x es una columna con el formato de 
6   % las tablas anteriores
7   x=zeros(n,2);
8   x0=a;
9   x(1,1)=0.5*(x0+p/x0);
10  x(1,2)=abs(x(1,1)-sqrt(p));
11  for i = 2:n
12    x(i,1)=0.5*(x(i-1)+p/x(i-1));
13    x(i,2)=abs(x(i,1)-sqrt(p));
14  end
15  end

3.2. Demostración de la convergencia

Vamos a demostrar que, en efecto, la sucesión

converge precisamente a la raíz cuadrada de p.

Usaremos el Teorema de la Convergencia Monótona, que dice así:

Necesitamos demostrar que

1. la sucesión está acotada (inferiormente),
2. y que es decreciente.

a) La sucesión está acotada inferiormente por la raíz de p:

Como la última desigualdad siempre se cumple, la primera también.

b) La sucesión es monótona decreciente:

Sabemos que la última desigualdad es cierta (por el apartado anterior), por tanto, la primera también.

Finalmente, aplicando el Teorema de la Convergencia Monótona, la sucesión converge a la raíz cuadrada de p: