Cantor dust (Polvo de Cantor)

En esta página vamos a generar el fractal Cantor dust por la técnica de string rewriting que explicamos en la página String rewriting: Alfombra de Sierpiński. También, calcularemos la dimensión de Hausdorff de este fractal.
Otros fractales generados por string rewriting:
El fractal Cantor dust es la versión bidimensional del conjunto de Cantor (también, existe la versión tridimensional). Al igual que el conjunto de Cantor, Cantor dust tiene medida cero.
Reglas
Las dos reglas que utilizamos para generar Cantor dust son las siguientes:
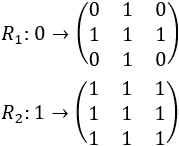
Recordamos que representamos el símbolo 1 como un cuadrado blanco y el símbolo 0 como un cuadrado negro.
Cantor dust (Polvo de Cantor)
Comenzamos con el símbolo 0 (iteración \(n=0\)), que es un cuadrado negro de lado 1:

Iteración \(n=1\):

Iteración \(n=2\):

Iteración \(n=3\):

Iteración \(n=4\):

Iteración \(n=5\):

Dimensión de Hausdorff
Sean \(N_n\) el número de cuadrados negros y \(L_n\) el lado de los cuadrados en la iteración \(n\). Entonces, la dimensión de Hausdorff del fractal es el siguiente límite:
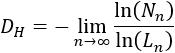
Observando las figuras:
Por tanto, deducimos
La dimensión de Hausdorff del fractal es
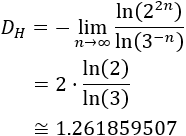
El área del fractal es nula ya que el área en cada iteración es
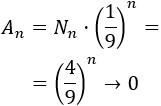
Referencias
-
Mandelbrot, B. B. The Fractal Geometry of Nature. New York: W. H. Freeman, p. 80, 1983.
-
Ott, E. Chaos in Dynamical Systems. New York: Cambridge University Press, pp. 103-104, 1993.
Cantor dust (Polvo de Cantor) - © matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.


