Fractal de Vicsek (Box fractal)


En esta página vamos a generar el fractal de Vicsek (o box fractal) por la técnica de string rewriting que explicamos en la página String rewriting: Alfombra de Sierpiński. También, calcularemos el área, la dimensión de Hausdorff-Besicovitch y el perímetro de este fractal.
Otros fractales generados por string rewriting:
Para generar el fractal de Vicsek, comenzamos con el cuadrado unidad (de color negro). En cada iteración, el/los cuadrados los dividimos en otros 5 cuadrados iguales siguiendo un patrón. Los lados de los cuadrados en cada iteración miden una tercera parte de lo que miden en la iteración anterior.
Reglas
Para la primera versión del fractal utilizamos las siguientes reglas de sustitución:
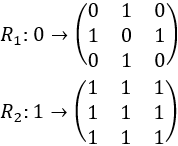
Recordamos que representamos el símbolo 1 como un cuadrado blanco y el símbolo 0 como un cuadrado negro.
Fractal de Vicsek
Comenzamos con el símbolo 0 (iteración \(n=0\)), que es un cuadrado negro de lado 1:

Iteración \(n=1\):

Iteración \(n=2\):

Iteración \(n=3\):

Iteración \(n=4\):

Iteración \(n=5\):

Dimensión de Hausdorff
Sean \(N_n\) el número de cuadrados negros y \(L_n\) el lado de los cuadrados en la iteración \(n\). Entonces, la dimensión de Hausdorff del fractal es el siguiente límite:
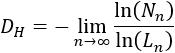
Observando las figuras:
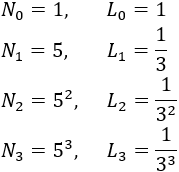
Por tanto, deducimos
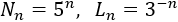
La dimensión de Hausdorff del fractal es
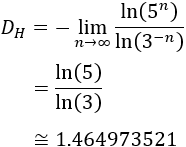
Área y perímetro
El área del fractal es nula ya que el área en cada iteración es
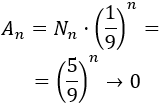
El perímetro del fractal es infinito ya que el perímetro en cada iteración es
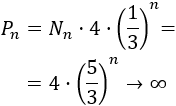
Fractal de Vicsek (2)
Para la primera versión del fractal utilizamos las siguientes reglas de sustitución:
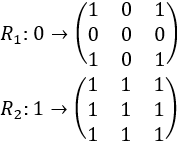
Comenzamos con el símbolo 0 (iteración \(n=0\)), que es un cuadrado negro de lado 1:

Iteración \(n=1\):

Iteración \(n=2\):

Iteración \(n=3\):

Iteración \(n=4\):

Iteración \(n=5\):

Referencias
-
Sloane, N. J. A. Sequences A000351/M3937 and A113209 in The On-Line Encyclopedia of Integer Sequences.
Fractal de Vicsek (box fractal)- © matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.


