logotipo matesfacil

String Rewriting: Alfombra de Sierpiński

Explicamos el método de String Rewriting para generar las sucesivas iteraciones de fractales. Generamos, a modo de ejemplo, la alfombra de Sierpinski (Sierpinski carpet) y calculamos su dimensión de Hausdorff. Fractal. Fractales.

En esta página vamos a ver una forma sencilla de generar fractales bidimensionales llamada String rewriting. Este método consiste en sustituir cadenas según una o varias reglas de sustitución. Generaremos la alfombra de Sierpiński y calcularemos su dimensión de Hausdorff. Otros ejemplos:

El método

Sea el alfabeto de dos símbolos \(\Sigma = \{0,1\}\). Trabajaremos con matrices cuadradas sobre \(\Sigma\).

Las dos únicas matrices dimensión 1 posibles son

Explicamos el método de String Rewriting para generar las sucesivas iteraciones de fractales. Generamos, a modo de ejemplo, la alfombra de Sierpinski (Sierpinski carpet) y calculamos su dimensión de Hausdorff. Fractal. Fractales.

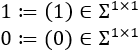
Un ejemplo de matriz de dimensión 2 sobre \(\Sigma\) es

Explicamos el método de String Rewriting para generar las sucesivas iteraciones de fractales. Generamos, a modo de ejemplo, la alfombra de Sierpinski (Sierpinski carpet) y calculamos su dimensión de Hausdorff. Fractal. Fractales.

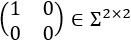
Una matriz de dimensión 1 la representamos como un cuadrado de lado \(L\). Si es la matriz 0, el cuadrado es de color negro. Si es la matriz 1, el cuadrado es blanco.

Una matriz de dimensión \(n\) la representamos como una cuadrícula de lado \(L\) formada por \(n×n\) cuadrados. Es decir, cada cuadrado es de lado \(L/n\).

Cada cuadrado de la cuadrícula lo identificamos con un elemento de la matriz. Por ejemplo, para una matriz de dimensión 3, la correspondencia entre los cuadrados y los elementos de la matriz es

Explicamos el método de String Rewriting para generar las sucesivas iteraciones de fractales. Generamos, a modo de ejemplo, la alfombra de Sierpinski (Sierpinski carpet) y calculamos su dimensión de Hausdorff. Fractal. Fractales.

Si el elemento \((i,j)\) de la matriz es 0, el cuadrado es de color negro. Si es 0, el cuadrado es blanco.


La alfombra de Sierpiński

Para generar la alfombra de Sierpinski, utilizamos dos reglas siguientes:

Explicamos el método de String Rewriting para generar las sucesivas iteraciones de fractales. Generamos, a modo de ejemplo, la alfombra de Sierpinski (Sierpinski carpet) y calculamos su dimensión de Hausdorff. Fractal. Fractales.

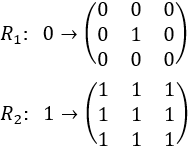
Al aplicar la regla \(R_1\), cada cuadrado negro de lado \(L_i\) se divide en una cuadrícula de 3x3 cuadrados de lado \(L_{i+1}=L_i/3\). El color de cada cuadrado viene dado por los elementos de la matriz.

Al aplicar la regla \(R_2\), cada cuadrado blanco de lado \(L_i\) se divide en una cuadrícula de 3x3 cuadrados de lado \(L_{i+1}=L_i/3\). El color de todos estos cuadrados es blanco.

Construimos el fractal

Iteración \(n=0\):

Comenzamos representado la matriz 0 como un cuadrado de lado \(L_0=1\) de color negro:

Explicamos el método de String Rewriting para generar las sucesivas iteraciones de fractales. Generamos, a modo de ejemplo, la alfombra de Sierpinski (Sierpinski carpet) y calculamos su dimensión de Hausdorff. Fractal. Fractales.

Iteración \(n=1\):

Aplicamos la regla \(R_1\) sobre la matriz anterior. Obtenemos una matriz 3x3:

Explicamos el método de String Rewriting para generar las sucesivas iteraciones de fractales. Generamos, a modo de ejemplo, la alfombra de Sierpinski (Sierpinski carpet) y calculamos su dimensión de Hausdorff. Fractal. Fractales.

Nota: no hemos aplicado R_2 porque no tenemos la matriz 1.

Iteración \(n=2\):

Aplicamos las reglas \(R_1\) y \(R_2\) sobre la matriz anterior:

Explicamos el método de String Rewriting para generar las sucesivas iteraciones de fractales. Generamos, a modo de ejemplo, la alfombra de Sierpinski (Sierpinski carpet) y calculamos su dimensión de Hausdorff. Fractal. Fractales.

Iteración \(n=3\):

Explicamos el método de String Rewriting para generar las sucesivas iteraciones de fractales. Generamos, a modo de ejemplo, la alfombra de Sierpinski (Sierpinski carpet) y calculamos su dimensión de Hausdorff. Fractal. Fractales.

Iteración \(n=4\):

Explicamos el método de String Rewriting para generar las sucesivas iteraciones de fractales. Generamos, a modo de ejemplo, la alfombra de Sierpinski (Sierpinski carpet) y calculamos su dimensión de Hausdorff. Fractal. Fractales.

Iteración \(n=5\):

Explicamos el método de String Rewriting para generar las sucesivas iteraciones de fractales. Generamos, a modo de ejemplo, la alfombra de Sierpinski (Sierpinski carpet) y calculamos su dimensión de Hausdorff. Fractal. Fractales.

Dimensión de Hausdorff

Sean \(N_n\) el número de cuadrados negros y \(L_n\) el lado de los cuadrados en la iteración \(n\). Entonces, la dimensión de Hausdorff del fractal es el siguiente límite:

Explicamos el método de String Rewriting para generar las sucesivas iteraciones de fractales. Generamos, a modo de ejemplo, la alfombra de Sierpinski (Sierpinski carpet) y calculamos su dimensión de Hausdorff. Fractal. Fractales.

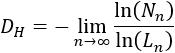
Observando las figuras:

Explicamos el método de String Rewriting para generar las sucesivas iteraciones de fractales. Generamos, a modo de ejemplo, la alfombra de Sierpinski (Sierpinski carpet) y calculamos su dimensión de Hausdorff. Fractal. Fractales.

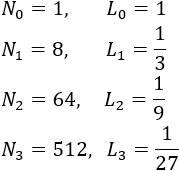
Por tanto, deducimos

Explicamos el método de String Rewriting para generar las sucesivas iteraciones de fractales. Generamos, a modo de ejemplo, la alfombra de Sierpinski (Sierpinski carpet) y calculamos su dimensión de Hausdorff. Fractal. Fractales.

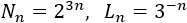
La dimensión de Hausdorff del fractal es

Explicamos el método de String Rewriting para generar las sucesivas iteraciones de fractales. Generamos, a modo de ejemplo, la alfombra de Sierpinski (Sierpinski carpet) y calculamos su dimensión de Hausdorff. Fractal. Fractales.

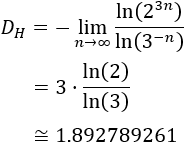
Ya calculamos en dimensiones de semejanza y de Hausdorff la dimensión de Hausdorff de este fractal.


Área

El área de la alfombra de Sierpinski es nula:

El área en la iteración \(n\) es

$$ A_n = \left( \frac{8}{9}\right)^n \rightarrow 0$$


Referencias

  • Reiter, C. A. Sierpiński Fractals and GCDs. Computers and Graphics 18, 885-891, 1994.

  • Sierpiński, W. On Curves Which Contain the Image of Any Given Curve. Mat. Sbornik 30, 267-287, 1916. Reprinted in Oeuvres Choisies, Vol. 2, pp. 107-119.




acceso al foro

ejercicios interactivos de matemáticas


String Rewriting: Alfombra de Sierpiński - © matesfacil.com

Creative Commons License
Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.