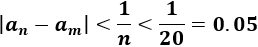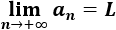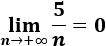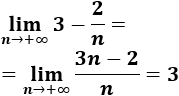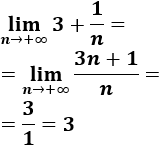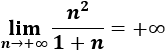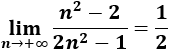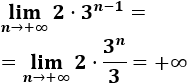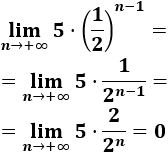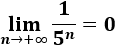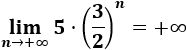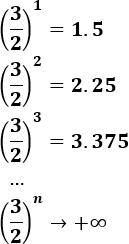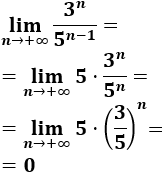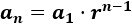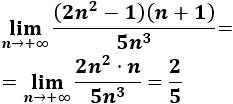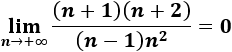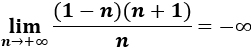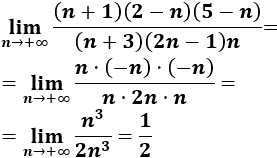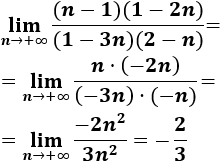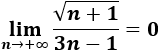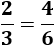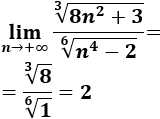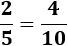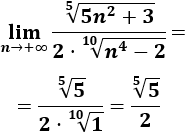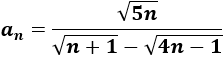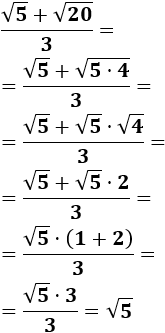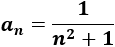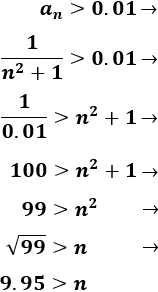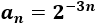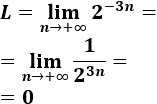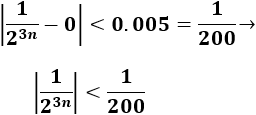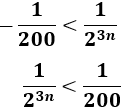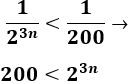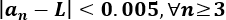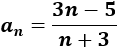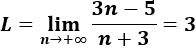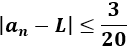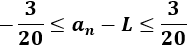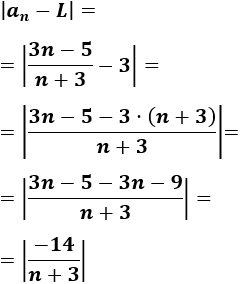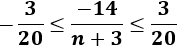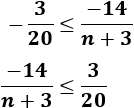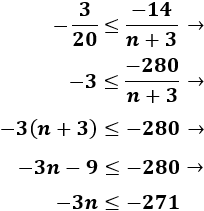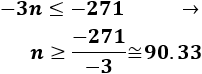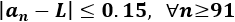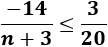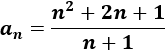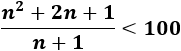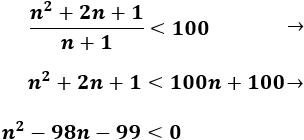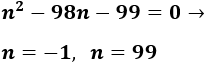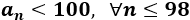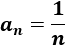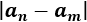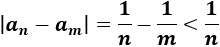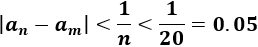Problema 1
Calcular, si existe, el límite de las siguientes sucesiones de cocientes polinomiales:
-
\( a_n= 5/n \)
-
\( a_n= 3 - \frac{2}{n}\)
-
\( a_n= 3 + \frac{1}{n}\)
-
\( a_n= \frac{n^2}{1+n}\)
-
\( a_n = \frac{n^2-2}{2n^2-1} \)
Ver solución
-
\( a_n= 5/n \)
El límite de la sucesión es 0 porque el grado del denominador es mayor que el del numerador:
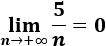
-
\( a_n= 3 - \frac{2}{n}\)
El límite de la sucesión es el cociente de los coeficientes directores del numerador y del denominador (porque tienen el mismo grado):
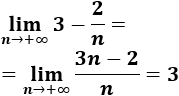
-
\( a_n= 3 + \frac{1}{n}\)
El límite de la sucesión es el cociente de los coeficientes directores del numerador y del denominador (porque tienen el mismo grado):
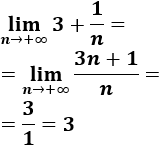
-
\( a_n= \frac{n^2}{1+n}\)
El límite de la sucesión es infinito porque el grado del numerador es mayor que el del denominador:
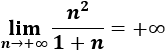
-
\( a_n = \frac{n^2-2}{2n^2-1} \)
El límite de la sucesión es el cociente de los coeficientes directores del numerador y del denominador (porque tienen el mismo grado):
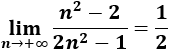
Problema 2
Determinar si las siguientes sucesiones geométricas convergen y calcular su límite:
-
\( a_n = 2\cdot 3^{n-1} \)
-
\( a_n = 5\cdot \left(1/2 \right)^{n-1} \)
-
\( a_n = \frac{1}{5^n} \)
-
\( a_n = 5\cdot \left(3/2 \right)^n \)
-
\( a_n = \frac{3^n}{5^{n-1}} \)
Ver solución
-
\( a_n = 2\cdot 3^{n-1} \)
La sucesión diverge:
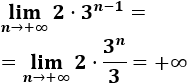
-
\( a_n = 5\cdot \left(1/2 \right)^{n-1} \)
La sucesión converge a 0:
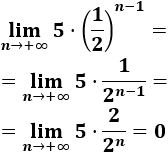
-
\( a_n = \frac{1}{5^n} \)
La sucesión converge a 0:
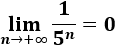
-
\( a_n = 5\cdot \left(3/2 \right)^n \)
La sucesión diverge:
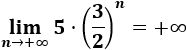
El límite es infinito porque 3/2 es mayor que 1 y, por tanto, sus potencias crecen:
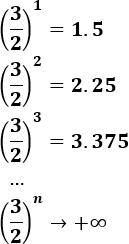
-
\( a_n = \frac{3^n}{5^{n-1}} \)
La sucesión converge a 0:
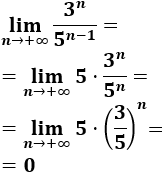
El límite es 0 porque 3/5 es menor que 1.
Problema 3 (dificultad alta)
Teniendo en cuenta el término general
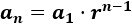
¿Cuándo es convergente una progresión geométrica?
Ayuda: considerar los siguientes casos:
-
Si \(r > 1\).
-
Si \(r=1\).
-
Si \(0< r < 1\).
-
Si \(r=0\).
-
Si \(-1 < r < 0\).
-
Si \(-1 ≤ r\).
Ver solución
El término general de una sucesión geométrica es
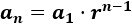
siendo \(r\) la razón de la sucesión, que es un valor constante.
El límite depende de la convergencia del factor \(r^{n-1}\):
-
Si \(r > 1\), el límite de \(r^{n-1}\) es \(+\infty \). La sucesión \(a_n\) diverge.
Por ejemplo, \(a_n=-(2^n)\rightarrow -\infty \).
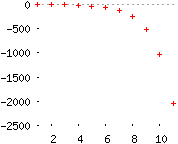
-
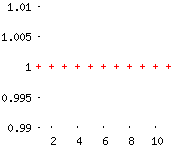
Si \(r=1\), la sucesión \(a_n\) converge por ser constante.
Por ejemplo, \(a_n=1^n\rightarrow 1\).
-
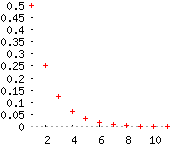
Si \(0< r < 1\), el límite de \(r^{n-1}\) es 0. La sucesión \(a_n\) converge a 0.
Por ejemplo, \(a_n=\left(1/2\right)^n\rightarrow 0\).
-
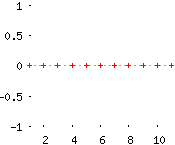
Si \(r=0\), la sucesión \(a_n\) converge a 0 por ser la sucesión constante \(a_n=0\).
-
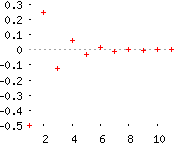
Si \(-1 < r < 0\), el límite de \(r^{n-1}\) es 0. La sucesión \(a_n\) es alternada y convergente a 0.
Por ejemplo, \(a_n=\left(-1/2\right)^n\rightarrow 0\).
-
Si \(-1 ≤ r\), el límite de \(r^{n-1}\) no existe. La sucesión \(a_n\) es alternada y divergente.
Por ejemplo, \(a_n=(-2)^n\rightarrow \pm \infty \).
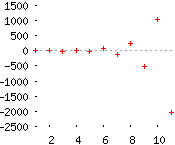
Problema 4
Calcular, si existe, el límite de las siguientes sucesiones:
-
\( a_n=\frac{(2n^2-1)(n+1)}{5n^3} \)
-
\( a_n = \frac{(n+1)(n+2)}{(n-1)n^2} \)
-
\( a_n = \frac{(1-n)(n+1)}{n} \)
-
\( a_n = \frac{(n+1)(2-n)(5-n)}{(n+3)(2n-1)n} \)
-
\( a_n = \frac{(n-1)(1-2n)}{(1-3n)(2-n)} \)
Ver solución
Para calcular el límite, tenemos que estudiar el grado de los polinomios del numerador y del denominador. Recordamos que cuando el grado es el mismo, el límite depende de los coeficientes directores de los polinomios.
-
\( a_n=\frac{(2n^2-1)(n+1)}{5n^3} \)
Como el grado del numerador y del denominador es 3, el límite es el cociente de los coeficientes directores:
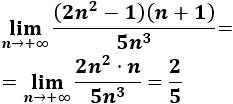
-
\( a_n = \frac{(n+1)(n+2)}{(n-1)n^2} \)
El límite es 0 porque el grado del denominador es mayor:
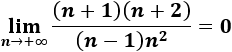
-
\( a_n = \frac{(1-n)(n+1)}{n} \)
La sucesión diverge porque el grado del numerador es mayor:
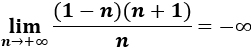
-
\( a_n = \frac{(n+1)(2-n)(5-n)}{(n+3)(2n-1)n} \)
La sucesión converge porque el grado del numerador y el del denominador es el mismo. Calculamos el límite:
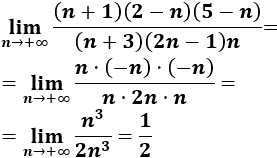
-
\( a_n = \frac{(n-1)(1-2n)}{(1-3n)(2-n)} \)
La sucesión converge porque el grado del numerador y el del denominador es el mismo. Calculamos el límite:
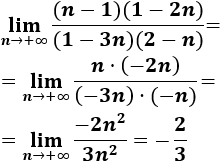
Problema 5
Calcular los límites de las siguientes sucesiones con raíces:
-
\( a_n = \frac{\sqrt{n+1}}{3n-1} \)
-
\( a_n = \frac{\sqrt[3]{8n^2+3}}{\sqrt[6]{n^4-2}} \)
-
\( a_n = \frac{\sqrt[5]{5n^2+3}}{2\cdot\sqrt[10]{n^4-2}} \)
Ver solución
-
\( a_n = \frac{\sqrt{n+1}}{3n-1} \)
El grado del numerador es 1/2 y el del denominador es 1. Por tanto, converge a 0:
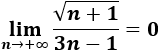
-
\( a_n = \frac{\sqrt[3]{8n^2+3}}{\sqrt[6]{n^4-2}} \)
El grado del numerador y el del numerador son el mismo:
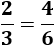
Por tanto,
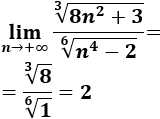
-
\( a_n = \frac{\sqrt[5]{5n^2+3}}{2\cdot\sqrt[10]{n^4-2}} \)
El grado del numerador y el del numerador son el mismo:
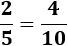
Por tanto,
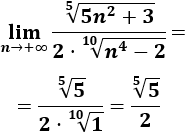
Problema 6
Hallar el límite de la siguiente sucesión:
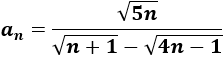
Ver solución
El grado del numerador y el del denominador son el mismo, pero tal y como está escrita la sucesión, no sabemos cuál es el coeficiente director del denominador. Tenemos que operar un poco (multiplicar y dividir por el conjugado del denominador):

En la última igualdad hemos simplificado el resultado:
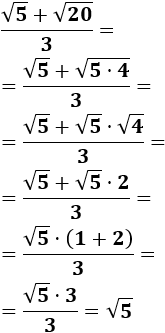
Problema 7
¿Cuántos términos de la sucesión \(a_n\) son mayores que 0.01?
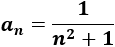
Ver solución
Tenemos que resolver la siguiente inecuación:
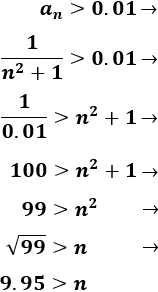
Los 9 primeros términos de la sucesión son mayores que 0.01.
Problema 8
¿A partir de qué \(n\) natural se cumple que la distancia entre los términos de la sucesión \(a_n\) y su límite \(L\) es menor que 0.005?
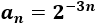
Nota: la distancia entre \(a_n\) y \(L\) es \(d= |a_n - L|\).
Ayuda: Inecuaciones con valor absoluto.
Ver solución
El límite de la sucesión es
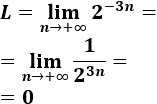
Tenemos que resolver la inecuación
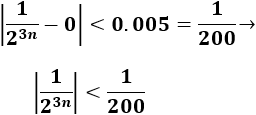
Como hay un valor absoluto, tenemos dos inecuaciones:
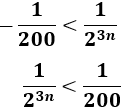
La primera siempre se cumple porque el término de la derecha es positivo para todo \(n\). Resolvemos la segunda:
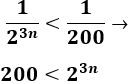
La solución de la inecuación es \(n\geq 3\). Por tanto,
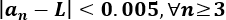
Problema 9 (dificultad alta)
¿A partir de qué natural se cumple que la distancia entre los términos de la sucesión \(a_n\) y su límite \(L\) es menor o igual que 0.15?
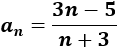
Ver solución
Calculamos el límite:
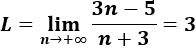
La distancia entre el término \(a_n\) y \(L\) es \(|a_n-L|\). Como queremos que esta distancia sea menor o igual que \(0.15=3/20\), tenemos que resolver la inecuación
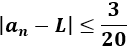
Recordad que para eliminar el valor absoluto podemos escribir
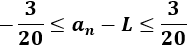
Calculamos la distancia entre \(a_n\) y \(L\):
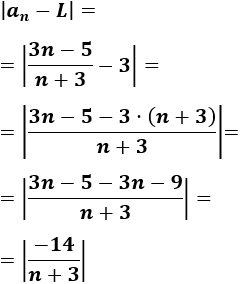
Por tanto, la inecuación del problema es
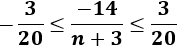
Descomponemos la inecuación en otras dos:
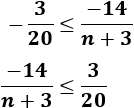
Resolvemos la primera:
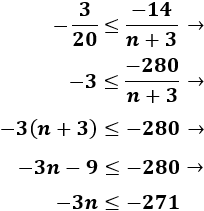
Al pasar el coeficiente -3 al otro lado tenemos que cambiar el signo de la desigualdad (porque es negativo):
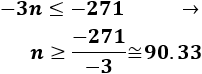
El primer natural mayor que 90.33 es \(n=91\). Por tanto,
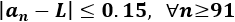
Resolvemos la segunda inecuación:
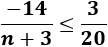
Como el lado izquierdo es negativo y el derecho es positivo, la igualdad siempre se cumple. Esta inecuación no nos aporta nada.
Por tanto, a partir de \(n=91\), la distancia entre el término \(a_n\) y el límite de la sucesión \(L=3\) es menor o igual que 0.15.
Problema 10 (dificultad alta)
¿Cuántos términos de la sucesión \(a_n\) son menores que 100?
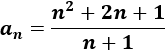
Nota: debe resolverse una inecuación de segundo grado.
Ver solución
Los términos que son menores que 100 son los que cumplen
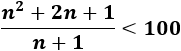
Resolvemos la inecuación:
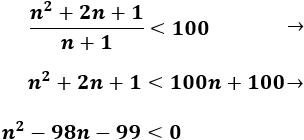
Resolvemos la ecuación de segundo grado asociada:
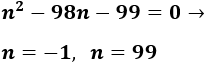
Al estudiar el signo, se obtiene que la solución de la inecuación es \(-1< n < 99\). Por tanto, los términos de la sucesión que son menores que 100 son los 98 primeros:
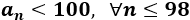
Problema 11 (dificultad alta)
Sea la sucesión
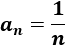
Comprobar que si \(n\) y \(m\) son mayores que 20, entonces la diferencia entre los términos \(a_n\) y \(a_m\) es menor que 0.05.
Nota: esta propiedad de las sucesiones tiene nombre: sucesión de Cauchy.
Ver solución
La diferencia entre los términos \(a_n\) y \(a_m\) es
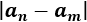
Vamos a suponer que \(m> n\) para eliminar el valor absoluto (porque \(a_m< a_n\)):
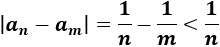
Por tanto, sabemos que la diferencia entre los términos \(a_n\) y \(a_m\) es menor que \(1/n\). Si \(n\) y \(m\) son mayores que 20, entonces