Curvas de von Koch

Esta página está dedicada a la curva de von Koch. Explicamos cómo construir este fractal y calculamos su dimensión fractal. Posteriormente, realizamos modificaciones para obtener fractales similares.
Contenido de esta página:
- Introducción
- Construcción de la curva de Koch
- Dimensión de Hausdorff de la curva
- Variantes de la curva
- Fractal de Cesàro
- (n,c)-curvas de von Koch
- La salchicha de Minkowski
- Copos y anticopos
Páginas relacionadas
Páginas amigas:
1. Introducción
La curva de von Koch fue descrita por el matemático sueco Helge von Koch en 1904 en [1] con la finalidad de proporcionar un ejemplo intuitivo de una función continua no diferenciable en ningún punto (demostración geométrica de la no diferenciabilidad en [2]).
Recordad que, intuitivamente, una función no es diferenciable en los puntos que forman codos (ángulos), como ocurre con la función valor absoluto, \(f(x)=|x|\), en el punto \(x=0\):
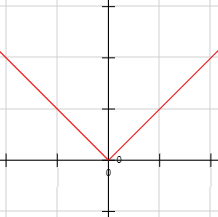
La curva de Koch se construye precisamente creando codos en todos los puntos para conseguir la no diferenciabilidad. En cada paso de su construcción (en cada iteración), se crea un codo en cada uno de los segmentos rectos:

2. Construcción de la curva de von Koch
Como se explica en Fractales autosemejantes, la curva de von Koch es un fractal autosemejante y es el atractor de un sistema de cuatro funciones iteradas contractivas con razón 1/3.
El conjunto inicial es un segmento de longitud L (iteración \(n=0\)):

En el primero paso (iteración \(n=1\)), se divide el segmento del paso anterior en tres segmentos de longitud L/3 y se sustituye el segmento central por los dos lados de un triángulo equilátero de lado L/3 (sin la base):
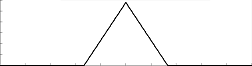
En los siguientes pasos, se repite el proceso del paso anterior en cada uno de los segmentos. Con tan solo 5 pasos ya se observa la estructura del fractal:
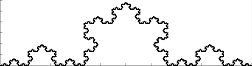
3. Dimensión de Hausdorff de la curva
En la primera iteración, el conjunto está formado por 4 segmentos. Estos segmentos son copias a escala 1/3 del conjunto del paso anterior (segmento de longitud L), situadas en distintos puntos del plano.
Del mismo modo, en las siguientes iteraciones, el conjunto está formado por cuatro copias a escala 1/3 del conjunto de la iteración anterior.
En los fractales autosemejantes en los que cada iteración se construye con \(N\) copias a escala \(1/r\) con \(0<r< 1\), la dimensión de Hausdorff-Besicovitch es
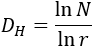
Por tanto, la dimensión de Hausdorff-Besicovitch de la curva de Koch es
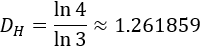
4. Variantes de la curva
El conjunto inicial para construir la curva de Koch es el segmento de longitud L=1 (normalmente, se utiliza L=1). En la primera iteración, dos de las cuatro copias a escala 1/3 constituyen un codo. Este codo forma ángulos de 60 grados con las otras copias:
Si variamos el ángulo, se obtienen otros fractales.
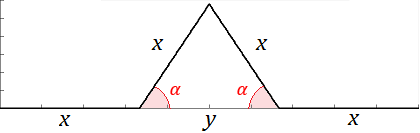
Si cambiamos el ángulo, tenemos que cambiar la longitud del segmento intermedio que se elimina (para que los lados del triángulo midan lo mismo que los segmentos laterales). Observad que, entonces, el trángulo que se forma es isósceles no equilátero. A continuación, construimos varias curvas variando el ángulo \(\alpha\) y calculamos su dimensión de Hausdorff-Besicovitch.
Observando la figura, obtenemos las siguientes relaciones:

Aplicando trigonometría básica,
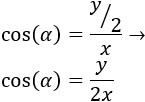
Sustituyendo,
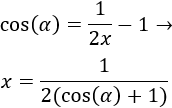
Como \(x\) es la razón de contracción en cada iteración, ya sabemos que la dimensión de Hausdorff de la variante del fractal con ángulo \(\alpha\) es
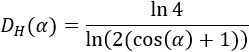
5. Fractal de Cesàro

El fractal de Cesàro es una de las variantes más conocidas de la curva de Koch. Se construye con ángulo \(60^\circ < \alpha < 90^\circ\). Por tanto, la dimensión de Hausdorff es
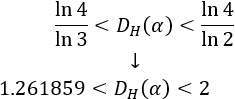
Por ejemplo, para 85°, la dimensión de Hausdorff del fractal es
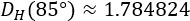
Animación con 7 iteraciones:

6. (n,c)-curvas de von Koch
Los fractales de los que hemos estado hablando se construyen sustituyendo un segmento central por un triángulo (sin la base). En [2], se define la (n,c)-curva de Koch, siendo \(0<c<1\) y \(n\) un natural, como el fractal que se construye comenzando por un segmento de longitud \(L\) (por comodidad, \(L=1\)) y que en cada iteración se sustituye el segmento central de longitud \(c·L\) por un polígono regular de \(n\) lados con lado \(c·L\).
Por ejemplo, la (4,1/3)-curva de Koch (curva de Koch cuadrática de tipo 1) se construye formando un cuadrado de lado 1/3:

La dimensión de Hausdorff de este fractal es
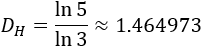
Según los parámetros \(n\) y \(c\), puede ocurrir que el fractal presente auto-intersecciones. En [2], se demuestra que la (n,c)-curva de von Koch no presenta auto-intersecciones si

cuando \(n\) es par o si
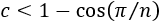
si \(n\) es impar.
Si la (n,c)-curva no tiene auto-intersecciones, como los dos segmentos laterales se contraen con razón \((1-c)/2\), la dimensión del fractal es el valor positivo \(s\) tal que
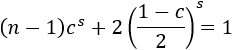
Por ejemplo, la (5,0.2)-curva de von Koch con 5 iteraciones es

La dimensión de Hausdorff de este fractal es, aproximadamente, 1.37898.
7. La salchicha de Minkowski
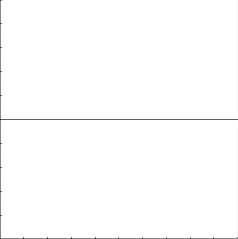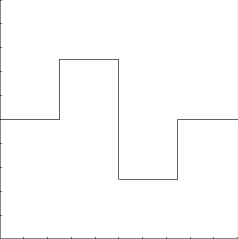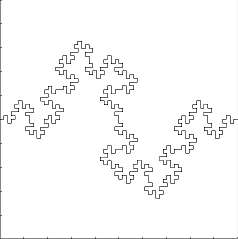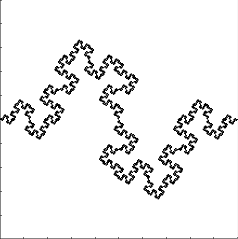
La salchicha de Minkowski (curva de Koch cuadrática de tipo 2) es una variante de la curva de von Koch. Para construirla, se divide cada segmento en otros cuatro y se sustituyen los dos segmentos centrales por dos cuadrados (sin base) con distinta orientación.
Animación con las 4 primeras iteraciones:
La dimensión de Hausdorff de este fractal es
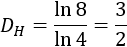
8. Copos y anticopos de von Koch
El copo de nieve de Koch (Koch snowflake) y el anticopo de nieve de Koch (Koch antisnowflake) son fractales que se construyen como las curvas de von Koch, pero con un polígono regular como conjunto inicial, en lugar de un segmento.
En los anticopos, el polígono que se forma en cada iteración está orientado hacia el centro del polígono, mientras que en los copos es al contrario.
De forma análoga a las curvas de von Koch, los llamamos (n,c)-copo y (n,c)-anticopo, siendo el conjunto inicial un polígono de \(n\) lados. En cada iteración, los segmentos cambian como lo hacen en las (n,c)-curvas.
Primeras iteraciones del (3,1/3)-von Koch snowflake:

Primeras iteraciones del (3,1/3)-von Koch antisnowflake:
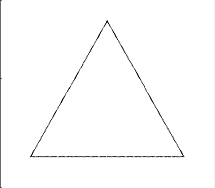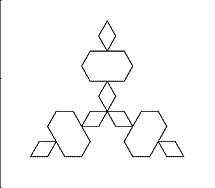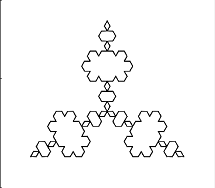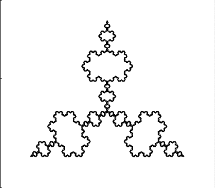
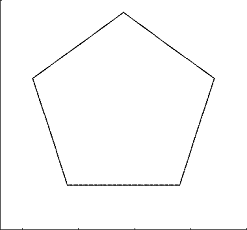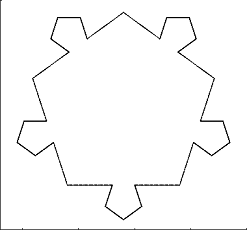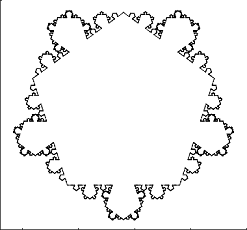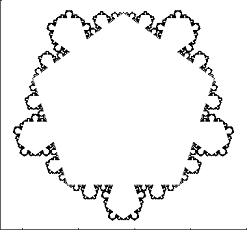
Primeras iteraciones del (5,0.2)-von Koch snowflake:
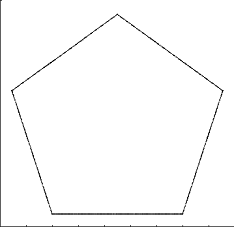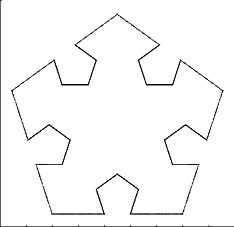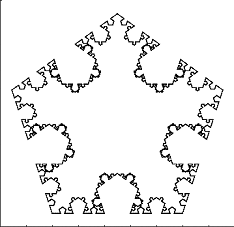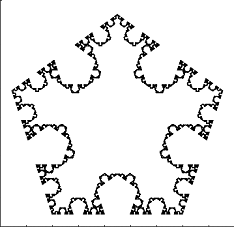
Primeras iteraciones del (5,0.2)-von Koch antisnowflake:
Referencias
- Koch, H. von. Sur une courbe continue sans tangente, obtenue par une construction géometrique élémentaire. Arkiv för Matematik Astronomi och Fysik 1 (1904) 681-704.
- Ungar, Sime. The Koch Curve: A Geometric Proof. The American Mathematical Monthly, Vol. 114, No. 1 (January 2007), 61-66.
Curvas de Koch - © matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.


