María Gaetana Agnesi y la bruja de Agnesi

En esta página proporcionamos una breve biografía de María Gaetana Agnesi y explicamos cómo se construye y una parametrización de la Bruja de Agnesi.

Contenido de esta página:

1. Biografía de María Gaetana Agnesi
2. Historia de la curva de Agnesi
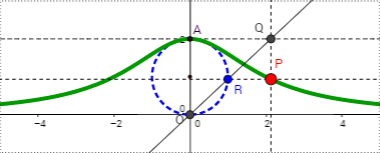
3. Construcción de la curva de Agnesi

María Gaetana Agnesi (1718-1799) nació en Milán (Italia) y fue la primera mujer en escribir un tratado de matemáticas como profesora de una universidad Es conocida por su obra Instituzioni analitiche ad uso della gioventù italiana publicada en 1748, cuya edición tuvo que costear ella misma.

El padre de María Agnesi, Pietro Agnesi, tuvo 21 hijos con sus tres esposas, de los cuales Agnesi era la mayor. Se dice que antes de sus quince años, Agnesi dominaba cinco idiomas (alemán, español, francés, griego y latín) además de italiano. Hay constancia de que el papa Benedicto XIV había elogiado la obra de Agnesi y que fue designada por éste para ocupar una cátedra en la Universidad de Bolgna.

En realidad, la Curva de Agnesi fue estudiada con anterioridad por el francés Pierre de Fermat (1607-1665) en el año 1630, aunque fue el italiano Luigi Guido Grandi (1671-1742) quien dio una construcción de la misma en 1703.

El nombre de "Bruja de Agnesi" se debe a María Agnesi, quien la estudió en su obra Instituzioni analitiche ad uso della gioventù italiana (1748). En este tratado, la curva es llamada la versiera (del latín verteré que significa girar o virar). Sin embargo, John Colson (1680-1760), Profesor Lucasiano de la Universidad de Cambridge, tradujo el tratado al inglés y confundió el término versiera con avversiera, cuyo significado es Adversario de Dios, sinónimo de bruja.

La curva está formada el conjunto de puntos \(P\) definidos como sigue:

1. \( R \) es un punto cualquiera de la circunferencia de radio 1 y centro \((0,1)\).

La curva parametrizada de la circunferencia de radio 1 y centro \( (0,1)\) es

$$ \alpha (t) = (sin(t), 1+cos(t)),$$

$$ t\in(-\pi ,\pi ).$$

Como \(R \) es un punto de \( \alpha\) su coordenadas son

$$ R = (sin(t),1+cos(t)) $$

2. El punto \( Q \) es el punto de intersección de la recta horizontal que pasa por el punto \( A =(1,2) \) y de la recta \( r\) que une al punto \(O = (0,0) \) con \( R\).

La recta \( r\) está formada por los puntos \( \lambda\cdot R\):

$$ r(t) = (\lambda\cdot sin(t), \lambda\cdot (1+cos(t))) $$

Como \( R\) está en \( r\), \( R \) será de la forma

$$ R = (\lambda\cdot sin(t), \lambda\cdot (1+cos(t))) $$

El punto intersección de \(r\) con la recta horizontal que pasa por \(A\) debe tener su segunda coordenada igual a 2. Luego

$$ 2 = \lambda\cdot (1+cos(t))) \rightarrow $$

$$ \rightarrow \lambda = \frac{2}{1+cos(t)} $$

Con lo que las coordenadas de \( Q\) son

$$ Q = \left( \frac{2sin(t)}{1+cos(t)}, 2\right) $$

3. El punto \( P \) es la intersección de la recta horizontal que pasa por el punto \( R\) y de la recta vertical que pasa por \( Q\).

La primera coordenada de \( P\) debe coincidir con la de \( Q\) y la segunda coordenada debe coincidir con la de \( R\). Por tanto,

$$ P = \left( \frac{2sin(t)}{1+cos(t)}, 1+cos(t)\right) $$

Por tanto, la ecuación paramétrica de la Bruja de Agnesi es

$$ \beta (t) = \left( \frac{2sin(t)}{1+cos(t)}, 1+cos(t)\right), $$

$$ t\in (-\pi, \pi )$$