Euclides y el quinto postulado
En esta página proporcionamos una breve biografía de Euclides de Alejandría y enunciamos sus cinco postulados. También, comentamos la importancia del quinto postulado y presentamos las geometrías que no lo consideran como axioma: las geometrías no euclídeas y las absolutas.
Contenido de esta página:
- Biografía de Euclides de Alejandría
- Quinto postulado de Euclides
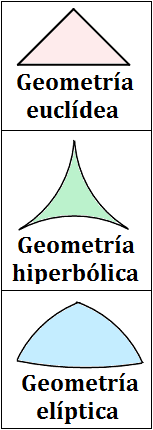
- Geometrías no euclídeas
- Geometrías absolutas
- Referencias
Páginas relacionadas
Otras páginas:
1. Biografía de Euclides de Alejandría
Euclides (o Euclides de Alejandría) fue un matemático griego que vivió, aproximadamente, entre los años 325 a. C. y 265 a. C. Es considerado el padre de la geometría, auqnue no se sabe exactamente si fue el autor real de todos sus textos o simplemente fueron firmados con su nombre por alguna razón desconocida.
Algunos investigadores piensan que no existió y que sus obras fueron firmadas con el nombre de Euclides en referencia al personaje histórico Euclides de Megara. Sin embargo, no existen suficientes evidencias para aceptar esta hipótesis.
Quizás la labor de Euclides no fue más que la de recopilar los numerosos resultados de la Antigüedad. Lo más sorprendente es que desarrolló la geometría por rigurosa deducción a partir de los axiomas y las definiciones.
Su obra más conocida, Elementos, es el segundo libro con más ediciones publicadas (después de la Biblia). Consta de 13 libros y el primero de ellos contiene 10 axiomas (5 postulados y 5 nociones) y 23 definiciones, a partir de los cuales se deducen 48 proposiciones entre las que se encuentra el famoso teorema de Pitágoras.