Producto de Matrices
En esta página vamos a ver cómo se define el producto de matrices.
Contenido de esta página:
- Introducción
- Recordatorio del producto de matrices y de sus propiedades
- 10 Ejercicios Resueltos: productos de matrices
Calculadoras de matrices:
Páginas relacionadas:
Páginas amigas:
Introducción
Probablemente, las matrices son el primer contacto que se tiene con elementos matemáticos cuyo producto no es conmutativo. Es decir, si \(A\) y \(B\) son dos matrices, no siempre se cumple \( A\cdot B = B \cdot A \). Como consecuencia, se pierden algunos resultados como, por ejemplo, la fórmula de Newton para el cuadrado de un binomio, que establece que para números reales
$$ (a+b)^2 = a^2+2ab+b^2 $$
Como para poder calcular el producto de matrices \(A\cdot B \) se requiere el número de columnas de \(A\) sea el mismo que el número de filas de \(B\), en ocasiones ni siquiera podemos considerar el producto \( B\cdot A\) .
En la sección se define la operación producto de matrices y se enumeran las propiedades básicas de la misma. Posteriormente, se plantean y resuelven problemas del producto de matrices (reales) de diferente dimensión y de matrices cuadradas.
Recordatorio
Definición del producto
Dadas dos matrices \(A\) y \( B \) de dimensiones \(m \times n\) y \(n \times p\), respectivamente, se define su producto \( A\cdot B \) como la matriz de dimensión \( m \times p\) tal que el elemento de la posición fila \(i\) y columna \( j \) es el resultado del producto de los vectores fila \(i\) de \(A\) y columna \(j\) de \(B\).
Matemáticamente, si las matrices son
$$ A = (a_{i,j})^{1\leq i \leq m}_{1\leq j \leq n}$$
$$ B = (b_{i,j})^{1\leq i \leq n}_{1\leq j \leq p} $$
entonces el producto \(A\cdot B\) es
$$ A\cdot B := ( m_{i,j})^{1\leq i \leq m}_{1\leq j \leq p} $$
siendo
$$ m_{i,j} := \sum_{k=1}^n {a_{i,k}\cdot b_{k,j}} $$
Consideraciones a tener en cuenta y propiedades:
-
Para poder efectuar el producto de matrices \( A\cdot B\), el número de columnas de \( A\) y el número de filas de \( B \) tiene que ser el mismo.
-
El producto de matrices no es necesariamente conmutativo, es decir, no siempre se cumple \(A \cdot B = B\cdot A\).
-
El producto de matrices es asociativo, es decir,
$$A \cdot ( B\cdot C ) = ( A\cdot B )\cdot C$$
El producto de matrices es distributivo respecto de la suma, es decir,
$$A \cdot ( B + C ) = A\cdot B + A\cdot C$$
-
El producto tiene elemento neutro, \( I_n\), que es la identidad de dimensión que corresponda y es el elemento neutro por derecha e izquierda (si la matriz es cuadrada, si no, el neutro por derecha e izquierda tiene distinta dimensión). Es decir,
$$ A\cdot I_n = I_m\cdot A$$
siendo \(m \times n\) la dimensión de \( A\).
Otras propiedades (como el producto de matrices diagonales o triangulares) en: ejercicios teóricos de matrices.
Temas similares: potencias de matrices.

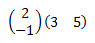
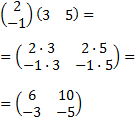
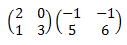
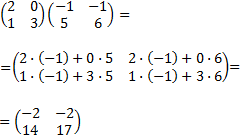
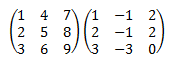
![calculamos el producto de dos matrices cuadradas de dimensión 3:
[1,4,7;2,5,8;3,6,9][1,-1,2;2,-1,2;3,-3,0] =
[30, -26, 10; 36, -31, 14; 42, -36, 18] definición del producto de matrices, propiedades y
ejemplos (ejercicios resueltos)](producto3-3.png)
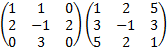
![calculamos el producto de dos matrices cuadradas de dimensión 3:
[1,1,0;2,-1,2;0,3,0][1,2,5;3,-1,3;5,2,1]=
[4, 1, 8; 9, 9, 9; 9, -3, 9] definición del producto de matrices, propiedades y
ejemplos (ejercicios resueltos)](producto4-3.png)
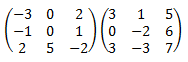
![calculamos el producto de dos matrices cuadradas de dimensión 3:
[-3,0,2;-1,0,1;2,5,-2][3,1,5;0,-2,6;3,-3,7]=
[-3, -9, -1; 0, -4, 2; 0, -2, 26] definición del producto de matrices, propiedades y
ejemplos (ejercicios resueltos)](producto5-3.png)
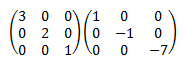
![calculamos el producto de dos matrices diagonales cuadradas de dimensión 3:
[3,0,0;0,2,0;0,0,1][1,0,0;0,-1,0;0,0,-7]=
[3, 0, 0; 0, -2, 0; 0, 0, -7] definición del producto de matrices, propiedades y
ejemplos (ejercicios resueltos)](producto6-3.png)
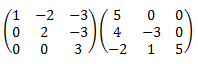
![calculamos el producto de dos matrices cuadradas de dimensión 3:
[1,0,0;0,-1,0;0,0,3][0,0,2;0,-1,0;1,0,0]=
[0, 0, 2; 0, 1, 0; 3, 0, 0] definición del producto de matrices, propiedades y
ejemplos (ejercicios resueltos)](producto7-3.png)
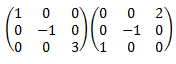
![calculamos el producto de dos matrices cuadradas de dimensión 3:
[1,0,0;0,-1,0;0,0,3][0,0,2;0,-1,0;1,0,0]=
[0, 0, 2; 0, 1, 0; 3, 0, 0] definición del producto de matrices, propiedades y
ejemplos (ejercicios resueltos)](producto8-3.png)
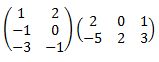
![calculamos el producto de las matrices de dimensiones (distintas) 3x2 y 2x3:
[1,2;-1,0;-3,-1][2,0,1;-5,2,3]=
[-8, 4, 7; -2, 0, -1; -1, -2, -6] definición del producto de matrices, propiedades y
ejemplos (ejercicios resueltos)](producto9-3.png)
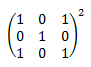
![calculamos el cuadrado de la matriz cuadrada de dimensión 3 calculando el producto de la matriz multiplicada consigo misma:
[1,0,1;0,1,0;1,0,1]^2=
[2, 0, 2; 0, 1, 0; 2, 0, 2] definición del producto de matrices, propiedades y
ejemplos (ejercicios resueltos)](producto10-3.png)

