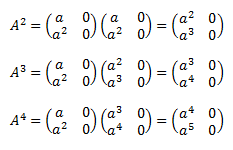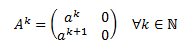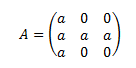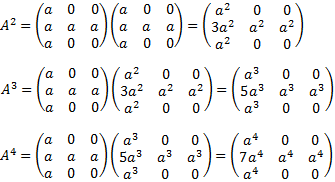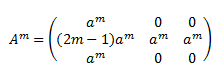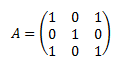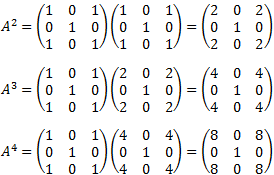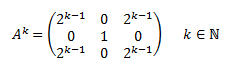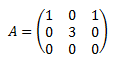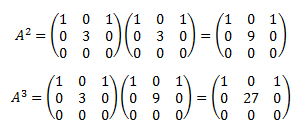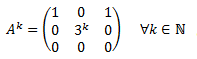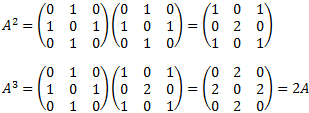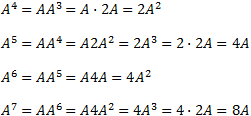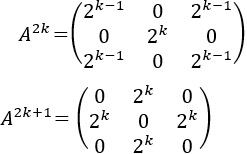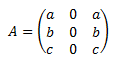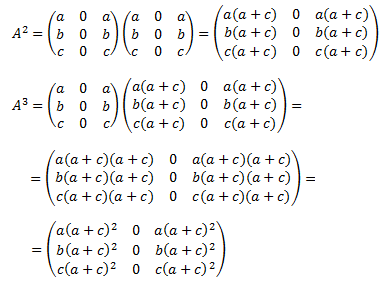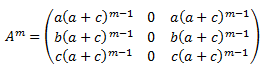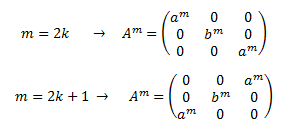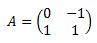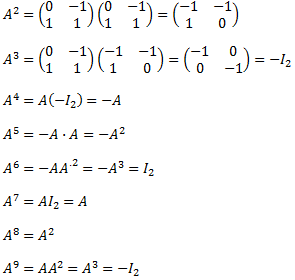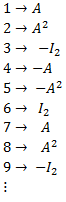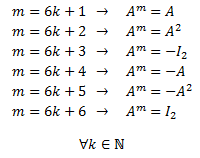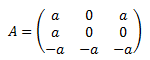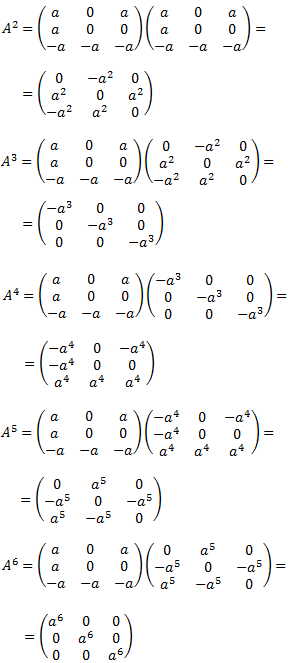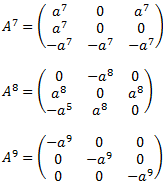Potencias de matrices
Contenido de esta página:
- Introducción
- 10 problemas resueltos
Páginas relacionadas
Páginas amigas:
Introducción
Antes que nada, debemos recordar que la potencia de una matriz no siempre se puede calcular. Sólo es posible cuando la matriz es cuadrada, es decir, cuando tiene el mismo número de filas que de columnas.
La peculiaridad de la potenciación de las matrices es que, en muchas matrices, las potencias siguen un patrón. Por ejemplo, las potencia \(n\)-ésima de una matriz diagonal \(A\) es también una matriz diagonal cuyos elementos de la diagonal son las potencias \(n\)-ésimas de los elementos de la diagonal de la matriz \(A\):
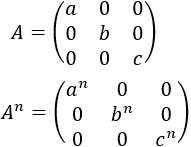
Por tanto, para muchas matrices, podemos encontrar una fórmula que nos proporcione la potencia \(n\)-ésima sin la necesidad de calcular todas las potencias.
Para encontrar esta fórmula, tenemos que fijarnos en:
-
La relación entre el exponente de la potencia y los elementos de la matriz. Por ejemplo, puede que algún elemento de la matriz sea el propio exponente.
-
La paridad del exponente. Por ejemplo, puede ocurrir que las potencias pares sean de una forma y las impares de otra.
-
Si hay distintos patrones. Por ejemplo, los exponentes múltiplos de un número pueden tener un patrón distinto a los que son múltiplos de otro.
La variación de los signos. Por ejemplo, las potencias pares y las impares pueden cambiar de signos.
- Repetición. Por ejemplo, puede haya varias matrices que se repiten consecutivamente.
En definitiva, para obtener la fórmula tenemos que observar las primeras potencias y emplear nuestra intuición. Normalmente, con el cálculo de las primeras 3 ó 5 potencias, podremos deducir la fórmula.