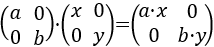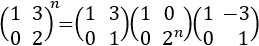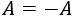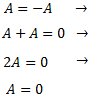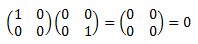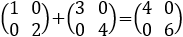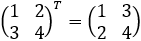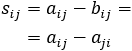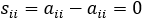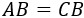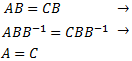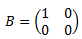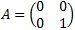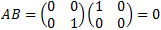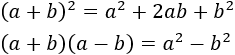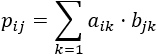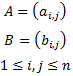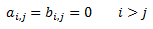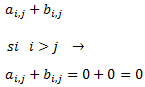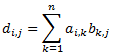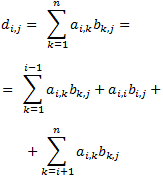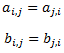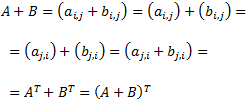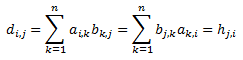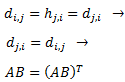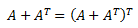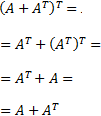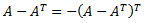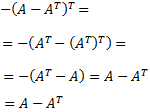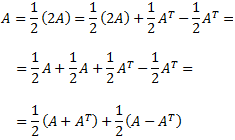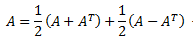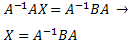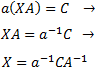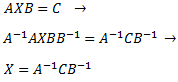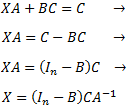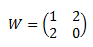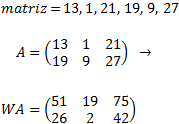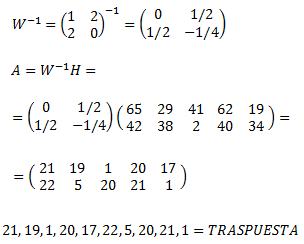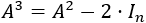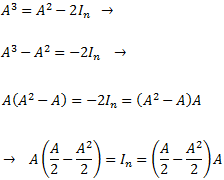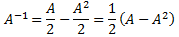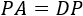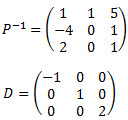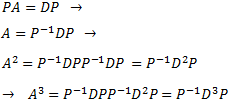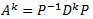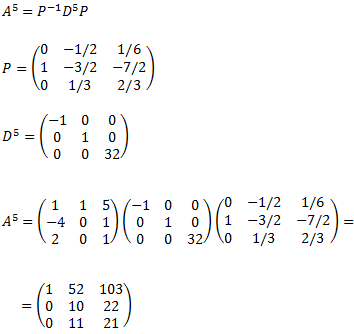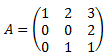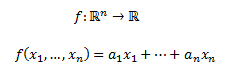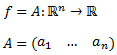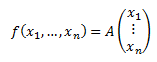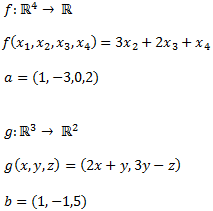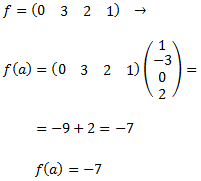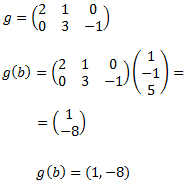Notación:
-
Denotaremos la matriz identidad de dimensión \(n\) como \(I_n\).
-
No siempre escribiremos el punto · de la multiplicación.
Problema 1
Demostrar que si una matriz \(A\) cumple
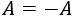
Entonces, \(A\) es la matriz nula (matriz de 0's).
Ver solución
La demostración es directa y es la misma que podemos aplicar a otro tipo de elementos matemáticos (como los números reales):
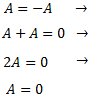
Problema 2
Sean \(A\) y \(B\) dos matrices cuadradas de dimensión \(n\) tales que su produco es la matriz nula, es decir, \(A·B = 0\). ¿Podemos afirmar que \(A\) ó \(B\) es la matriz nula?
Ver solución
Para demostrar que una propiedad no se cumple es suficiente dar un contraejemplo,
es decir, un caso particular para el que no se cumple la propiedad. En efecto, la propiedad no es cierta para matrices, al igual que otras propiedades de los reales relacionadas con el producto.
Veamos un contraejemplo:
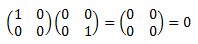
Las matrices anteriores se dice que son divisores de 0, una por la izquierda y la otra por la derecha.
Problema 2b
Demostrar que la suma y
la resta de dos matrices diagonales es una matriz diagonal.
Sean \(O\) la matriz de ceros, \(A\) una matriz de la misma dimensión y \(k\) un número real.
Demostrar que \(k·A = 0\) si, y sólo si,
\(k = 0\) ó \(A = O\).
-
Si \(A\) es una matriz diagonal de dimensión \(nxn\), ¿cuál
es la diagonal de \(A^T\) y la de \(A-A^T\)?
Ver solución
a. Como la suma de matrices se calcula sumando elementos en la misma posición, la suma dos matrices diagonales es también diagonal.
Por ejemplo,
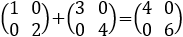
b. Si denotamos por \(a_{ij}\) al elemento de la fila \(i\) y columna \(j\) de la matriz \(A\), entonces, el elemento de la misma posición de la matriz \(k·A\) es \(k·a_{ij}\).
La única posibilidad de que \(k·A\) sea la matriz nula es que \(k=0\) o que todos los \(a_{ij}\) sean 0 y, por tanto, \(A=0\).
c. La matriz \(A^T\) es la traspuesta de \(A\). Es decir, si los elementos de \(A\) son \(a_{ij}\), los de \(A^T\) son \(b_{ij}=a_{ji}\).
La diagonal de \(A^T\) son los elementos \(b_{ii} = a_{ii}\). Es decir, tiene la misma diagonal que \(A\).
Por ejemplo,
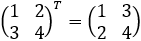
El elemento de la posición \((i,j)\) de la matriz \(A-A^T\) es
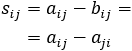
Los elementos de su diagonal son
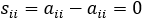
Por tanto, la diagonal de \(A-A^T\) está formada por 0's.
Problema 3
Sean \(A\), \(B\neq 0\) y \(C\) tres matrices cuadradas de dimensión \(n\) que cumplen la siguiente igualdad:
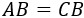
¿Se cumple que \(A = C\) ?
Ver solución
Si la matriz \(B\) es regular, es cierto porque que podemos multiplicar por la derecha de ambos lados de la igualdad por su inversa:
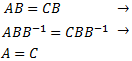
Esto nos hace pensar que no se cumple si \(B\) no es regular. Vamos a buscar un contraejemplo.
Consideremos la siguiente matriz singular (no regular):
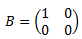
Sea la matriz
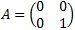
El producto \(AB\) es 0:
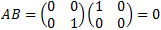
Si \(C\) es la matriz nula y \(B\) es otra matriz, entonces se cumple \(A·B = C·B = 0\), siendo \(A \neq C\). Por tanto, tenemos un contraejemplo.
Problema 4
Tenemos fórmulas para calcular el cuadrado de una suma de reales y el producto de una suma y una resta de reales:
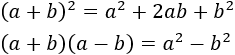
¿También se cumplen para matrices cuadradas?
Ver solución
Calculamos el cuadrado de la suma como el producto de la suma de matrices:
$$(A + B)^2 = (A + B)(A + B) =$$
$$= AA + AB + BA + BB =$$
$$= A^2 + B^2 + AB + BA $$
Para obtener la misma fórmula del binomio tenemos que sumar los dos últimos términos considerando
\(AB = BA\), es decir, considerando que el producto de matrices conmuta. Esto no siempre es así.
Procedemos del mismo modo para la segunda igualdad:
$$(A + B)(A - B) = A^2 - AB + BA - B^2$$
Por la misma razón, no podemos cancelar el segundo y el tercer término.
Las fórmulas son ciertas para matrices cuyo producto conmute, pero no lo son en general.
Problema 5
Demostrar que la suma y el producto de matrices diagonales es una matriz diagonal.
Ver solución
Sean \(a_{ij}\) y \(b_{ij}\) los elementos de la fila \(i\) y columna \(j\) de las matrices \(A\) y \(B\), respectivamente.
Entonces, el elemento de la fila \(i\) y columna \(j\) de la matriz suma \(A+B\) es
$$ s_{ij}= a_{ij}+b_{ij}$$
Como \(a_{ij}\) y \(b_{ij}\) son iguales a 0 si \(i\neq j\) (por ser diagonales), \(s_{ij} = 0 \) si \(i\neq j\). Así que la matriz \(A+B\) es diagonal.
El elemento de la fila \(i\) y columna \(j\) de la matriz producto \(AB\) es
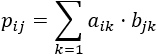
Pero como \(a_{ij}\) y \(b_{ij}\) son iguales a 0 si \(i\neq j\) (por ser diagonales), entonces todos los elementos de \(AB\) que no sean de la diagonal son 0. Por tanto, la matriz \(AB\) es diagonal.
Problema 6 (dificultad alta)
Demostrar que la suma y el producto de matrices triangulares superiores (inferiores) es una matriz triangular superior (inferior).
Ver solución
Vamos a utilizar la definición formal
del producto de matrices. Podéis demostrar la propiedad de una forma más sencilla e intuitiva para matrices con diemensiones pequeñas (como 2x2 ó 3x3).
Sean las matrices triangulares superiores de dimensión \(n\):
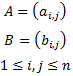
Como son triangulares superiores,
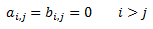
La matriz suma tiene en la posición \((i,j)\) al elemento
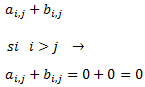
Y por tanto, la matriz suma es triangular superior.
El producto \(AB\) tiene en la posición \((i,j)\) al elemento
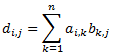
Vamos a escribir el sumatorio como una suma:
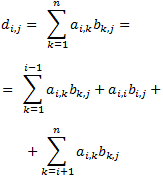
Supongamos \(i > j\):
$$ k\leq i-1 < i \rightarrow $$
$$ i > k $$
Por tanto, \(a_{i,k} = 0 \).
Luego el primer sumatorio es 0.
Por otro lado,
$$ k \geq i+1 > j+1 > j$$
Por tanto, \(b_{k,j} = 0\).
Con lo que el segundo sumatorio también es 0.
Además, como \(b_{i,j} = 0\),
$$ a_{i,i}·b_{i,j} = 0 $$
Por tanto, el producto es triangular superior.
Cambiando las desigualdades tenemos la demostración para triangulares inferiores.
Problema 7 (dificultad alta)
Demostrar que la suma de matrices simétricas es simétrica y que el producto
de simétricas es una matriz simétrica si el producto es conmutativo.
Ver solución
Una matriz cuadrada \(A =(a_{ij})\) es simétrica si \(A = A^T\), es decir, si \(a_{ij} = a_{ji}\).
Sean \(A=(a_{ij})\) y \(B=(b_{ij})\) matrices simétricas de la misma dimensión \(n\). Se tiene que
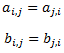
Calculamos la suma \(A+B\):
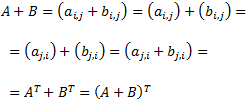
Supongamos ahora que \(A·B\ = B·A\). Queremos ver que \(AB = (AB)^T\).
El elemento de la posición \((i,j)\) del producto \(AB\) es
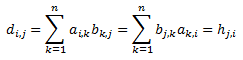
siendo \(h_{ji}\) el elemento de la posición \((j,i)\) del producto \(BA\).
Por hipótesis, \(AB = BA\), así que
$$ h_{j,i} = d_{j,i} $$
Junto con lo anterior tenemos
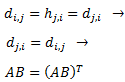
Problema 8
Demostrar que para toda matriz cuadrada \(A\), la matriz \(A+A^T\) es simétrica.
Ver solución
Una matriz cuadrada \(B\) es si métrica si \(B=B^T\). Por tanto, tenemos que demostrar
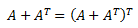
Pero esto es inmediato aplicando las propiedades de las traspuestas:
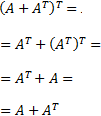
Problema 9
Demostrar que para toda matriz cuadrada \(A\), la matriz \(A-A^T\) es antisimétrica.
Nota: una matriz cuadrada \(B\) es antisimétrica si \(B = -B^T\).
Ver solución
Tenemos que demostrar la igualdad
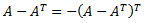
Aplicamos las propiedades de las matrices traspuestas:
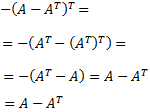
Problema 10
Demostrar que toda matriz cuadrada puede expresarse como suma de una matriz simétrica
y de una antisimétrica.
Ayuda: utilizad los dos problemas anteriores.
Ver solución
Por el Problema 8 sabemos que dada una matriz cuadrada \(A\), la matriz \(A + A^T\) es simétrica y, por el Problema 9, que \(A-A^T\) es antisimétrica.
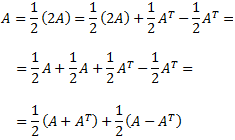
Por tanto, podemos escribir \(A\) como la suma de una simétrica y una antisimétrica como
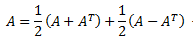
Problema 11 (ecuaciones matriciales)
Sean las matrices cuadradas \(A\), \(B\) y \(C\) de dimensión \(n\), siendo \(A\) y \(B\) regulares.
Calcular la matriz \(X\) de dimensión \(n\)
en cada caso:
\(AX = BA\)
\(a(XA) = C\), donde \(a\) es un real.
\(AXB = C\)
\(XA + BC = C\)
Ver solución
a. Multiplicando por la izquierda por la inversa de \(A\),
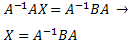
b. Si \(a = 0\), la igualdad sólo se cumple si \(C\) es la matriz nula y, en este caso, la matriz \(X\) puede ser cualquiera.
Si \(a \neq 0\), tiene inverso, y multiplicando por la izquierda por \(a^{-1}\) y por la derecha por \(A^{-1}\),
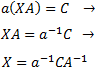
c. Multiplicando por la inversa de \(A\) por la izquierda y por la inversa de \(B\) por la derecha,
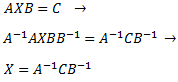
d. Aislamos \(XA\) a un lado y multiplicamos por la derecha por la inversa \(A^{-1}\):
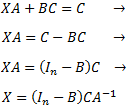
Problema 12
Podemos usar las matrices para codificar mensajes. Numeramos el alfabeto, por ejemplo, a=1, b=2, ... , z=27. Para la codificación nos ayudamos de una matriz:
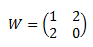
Escribiremos las palabras en matrices con 2 filas para poder multiplicarlas por la izquierda por \(W\).
Veamos un ejemplo: si la palabra es "matriz",
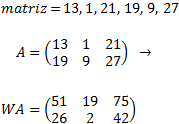
El mensaje codificado es la matriz \(WA\).
Se pide:
- ¿Cómo se descodifica una matriz?
- Si cambiamos de matriz de codificación, \(W\), ¿qué condición es necesaria para que el sistema funcione?
- ¿Qué mensaje contiene la siguiente matriz?

Ver solución
Para descodificar una matriz sólo debemos multiplicar por la izquierda por la inversa de \(W\). Por tanto, la condición que tenemos que exigir a \(W\) es que sea regular (para que exista su inversa).
La matriz codificada \(H\) es el producto \(W·A\).
Calculamos la matriz \(A\) que es la que contiene el mensaje. Para ello, multiplicamos por \(W^{-1}\):
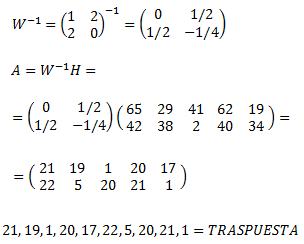
La matriz contiene el mensaje “traspuesta”.
Problema 13
Sea \(A\) la matriz regular que cumple
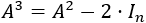
Hallar la inversa de \(A\) en función de \(A\).
Ver solución
Operando un poco,
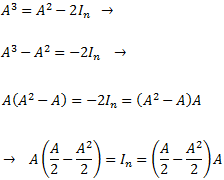
Por tanto, la inversa de \(A\) es
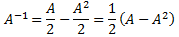
Problema 14
Decimos que una matriz \(A\) es diagonalizable con matriz de paso \(P\) si se cumple
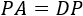
siendo \(D\) una matriz diagonal y \(P\) regular.
¿Por qué crees que es útil la diagonalización de una matriz para calcular sus potencias?
Calcular la potencia \(A^5\) sabiendo que \(PA =DP\) para las matrices
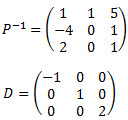
¿Cuál es la matriz \(A\)?
Ver solución
Supongamos que queremos calcular la potencia \(A^k\). Como la matriz \(P\) es regular, podemos multiplicar por su inversa:
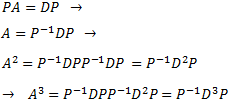
Es decir, por inducción,
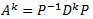
Y como \(D\) es diagonal, su potencia \(k\) es la matriz diagonal cuyos elementos son las potencias \(k\) de los elementos de \(D\). Así, las potencias de \(A\) se calculan rápidamente sin necesidad de calcular las \(k-2\) potencias anteriores.
Para las matrices dadas,
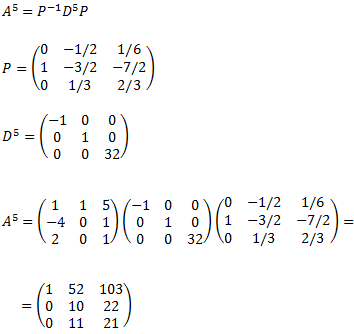
La matriz \(A\) la obtenemos fácilmente multiplicando por la izquierda por la inversa \(P^{-1}\) en \(PA = DP\):
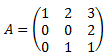
Problema 15
Considerar la siguiente función:
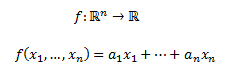
La podemos definir mediante una matriz fila \(A\):
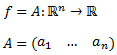
De este modo, la imagen de \(f\) es un producto matricial:
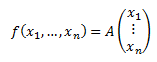
Encontrar las matrices que definen las siguientes funciones y calcular las imágenes de los puntos \(a\) y \(b\) dados:
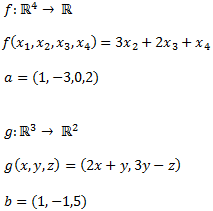
Ver solución
Para la función \(f\):
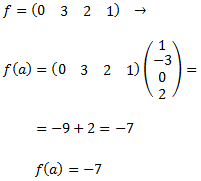
La función \(g\) se define mediante una matriz de dimensión \(2x3\):
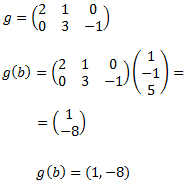


Problemas teóricos de matrices -
© matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.