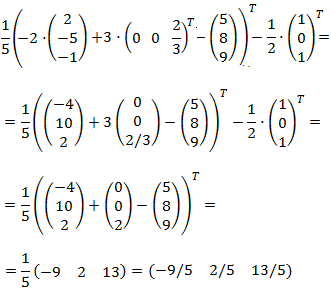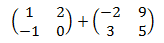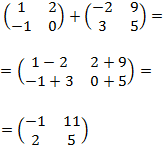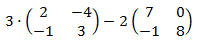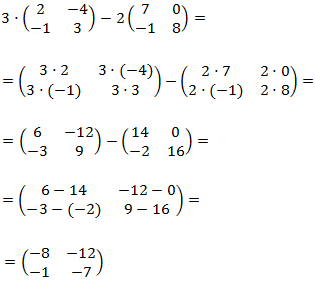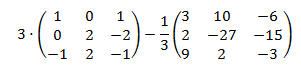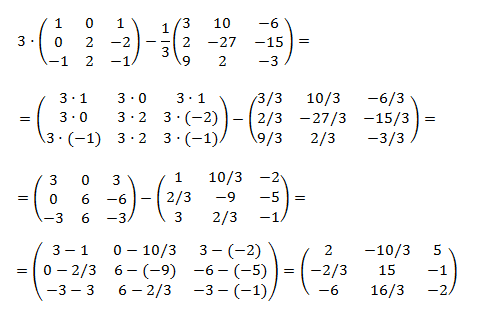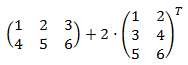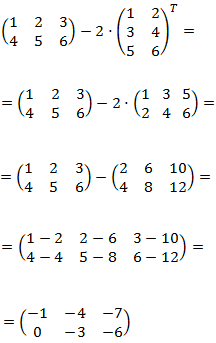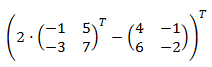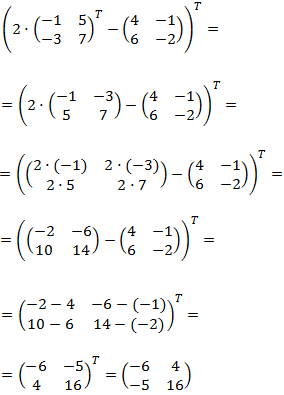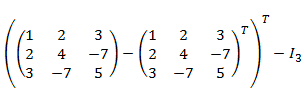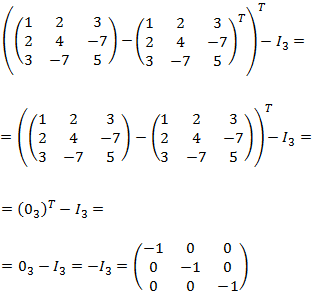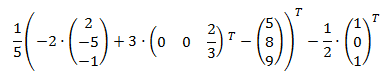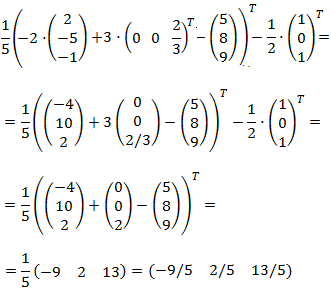En esta sección calculamos matrices transpuestas, sumas, restas y productos por escalares de matrices de distintas dimensiones.
Ejercicio 1
a) Suma de dos matrices cuadradas de dimensión 2:
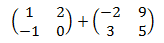
b) Suma de dos matrices rectangulares:
$$ \left(\begin{matrix}
1 & 2 & 0 \\
0 & 2 & 1
\end{matrix}\right) + \left(\begin{matrix}
1 & 0 & 1 \\
0 & 1 & 0
\end{matrix}\right) $$
c) Suma de dos matrices columna:
$$ \left(\begin{matrix}
1 \\
0 \\
3 \\
2
\end{matrix}\right) + \left(\begin{matrix}
-1 \\
0 \\
-2 \\
-1
\end{matrix}\right) $$
Solución
a) Tenemos que sumar los elementos que están en la misma posición. Por ejemplo, el elemento de la posición (1,1) de la matriz de la izquierda es 1 y en el de la matriz de la derecha es derecha es -2. Por tanto, en la posición (1,1) se la matriz suma escribimos la operación \(1+(-2)\).
Procedemos del mismo modo para todas las posiciones:
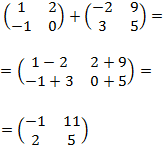
b) De forma análoga,
$$ \left(\begin{matrix}
1 & 2 & 0 \\
0 & 2 & 1
\end{matrix}\right) + \left(\begin{matrix}
1 & 0 & 1 \\
0 & 1 & 0
\end{matrix}\right) = $$
$$ =\left(\begin{matrix}
1+1 & 2+0 & 0+1 \\
0+0 & 2+1 & 1+0
\end{matrix}\right) = $$
$$ =\left(\begin{matrix}
2 & 2 & 1 \\
0 & 3 & 1
\end{matrix}\right) $$
c) Lo mismo para las matrices columna:
$$ \left(\begin{matrix}
1 \\
0 \\
3 \\
2
\end{matrix}\right) + \left(\begin{matrix}
-1 \\
0 \\
-2 \\
-1
\end{matrix}\right) =$$
$$ =\left(\begin{matrix}
1-1 \\
0+0 \\
3-2 \\
2-1
\end{matrix}\right)=$$
$$ =\left(\begin{matrix}
0 \\
0 \\
1 \\
1
\end{matrix}\right)$$
Ejercicio 2
a) Producto de una matriz rectangular por un escalar:
$$ 5\cdot \left(\begin{matrix}
1 & -2 & 0 \\
2 & -1 & -3
\end{matrix}\right) $$
b) Producto por un escalar y suma de dos matrices cuadradas de dimensión 2:
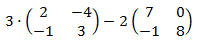
Solución
a) Multiplicamos todas las entradas de la matriz por el escalar:
$$ 5\cdot \left(\begin{matrix}
1 & -2 & 0 \\
2 & -1 & -3
\end{matrix}\right) =$$
$$ =\left(\begin{matrix}
5\cdot 1 & 5\cdot (-2) & 5\cdot 0 \\
5\cdot 2 & 5\cdot (-1) & 5\cdot (-3)
\end{matrix}\right) =$$
$$ =\left(\begin{matrix}
5 & -10 & 0 \\
10 & -5 & -15
\end{matrix}\right)$$
b) Al igual que haríamos con los números reales, primero calculamos
los productos y después la suma:
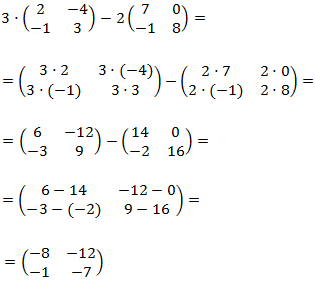
Ejercicio 3
Producto por un escalar y suma de dos matrices cuadradas de dimensión 3:
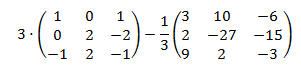
Solución
Procedemos del mismo modo que en el apartado anterior: primero calculamos los productos y después restamos las matrices:
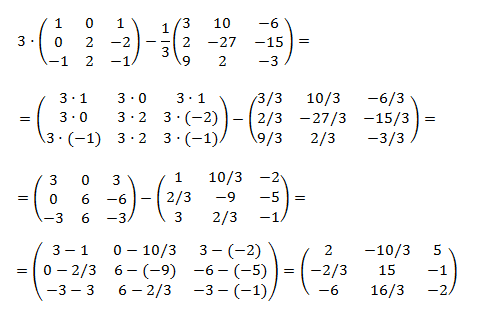
Ejercicio 4
a) Transpuesta de una matriz cuadrada de dimensión 2:
$$ \left(\begin{matrix}
1 & -2 \\
2 & -1
\end{matrix}\right)^T $$
b) Transpuesta de una matriz cuadrada de dimensión 3:
$$ \left(\begin{matrix}
0 & 1 & 1 \\
2 & -1 & -3 \\
0 & 2 & 5
\end{matrix}\right)^T $$
c) Transpuesta de una matriz rectangular (2x3):
$$ \left(\begin{matrix}
1 & 1 & 1 \\
2 & -2 & -3
\end{matrix}\right)^T $$
d) Transpuesta y suma de dos matrices rectangulares (2x3):
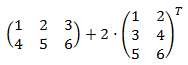
Solución
a) Cambiamos filas por columnas:
$$ \left(\begin{matrix}
1 & -2 \\
2 & -1
\end{matrix}\right)^T =$$
$$ =\left(\begin{matrix}
1 & 2 \\
-2 & -1
\end{matrix}\right)$$
Observad que la dimensión de las matrices es la misma porque son cuadradas.
b) Cambiamos filas por columnas:
$$ \left(\begin{matrix}
0 & 1 & 1 \\
2 & -1 & -3 \\
0 & 2 & 5
\end{matrix}\right)^T =$$
$$ =\left(\begin{matrix}
0 & 2 & 0 \\
1 & -1 & 2 \\
1 & -3 & 5
\end{matrix}\right) $$
Observard que los elementos de la diagonal mantienen su posición.
c) Cambiamos filas por columnas::
$$ \left(\begin{matrix}
1 & 1 & 1 \\
2 & -2 & -3
\end{matrix}\right)^T =$$
$$ =\left(\begin{matrix}
1 & 2 \\
1 & -2 \\
1 & -3
\end{matrix}\right) $$
Observad que la dimensión de la matriz es 2x3 y la de su transpuesta es 3x2.
d) En principo las matrices no pueden sumarse porque no tienen la misma
dimensión, pero al calcular la transpuesta de una de ellas, las dimensiones coinciden.
Primero calculamos la transpuesta y después sumamos las matrices:
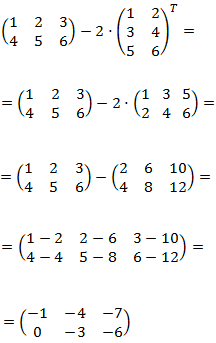
Ejercicio 5
Producto por un escalar, resta de dos matrices cuadradas y transposción:
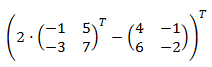
Solución
Primero simplificamos el contenido del paréntesis sumando las matrices. Después, calculamos la matriz transpuesta del resultado:
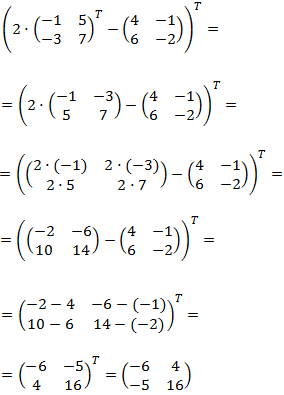
Ejercicio 6
Resta y transpuesta de matrices cuadradas de dimensión 3. \(I_3\) representa la matriz identidad de dimensión 3:
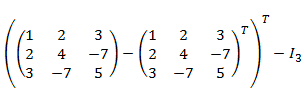
Solución
Recordamos que \(I_3\) es la matriz identidad de dimensión \( 3\times 3\).
Primero operamos dentro del paréntesis y después calculamos la transpuesta y la resta de matrices:
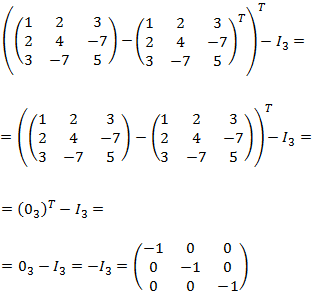
Ejercicio 7
Múltiples operaciones entre matrices columna (dimensión 3x1):
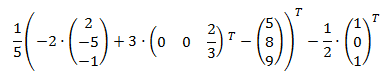
Solución
Las matrices son matrices fila y matrices columna.