Bolas, abiertos y cerrados de la topología usual

La topología usual sobre $\mathbb{R}^n$ puede definirse de varias formas. En esta página definimos los abiertos y cerrados de esta topología a partir de las bolas abiertas de la distancia euclídea. Proporcionamos ejemplos y algunas propiedades básicas.

Contenido de esta página:

Bola abierta
Bola cerrada
Conjunto abierto
Conjunto cerrado

Páginas relacionadas

Otras páginas:

1. Bola abierta

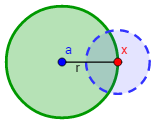
Sean $a = (a_1, a_2, ...,a_n)\in \mathbb{R}^n$ y $r> 0$. Llamamos bola abierta de centro $a$ y radio $r$ al conjunto

$$ B_r(a) := \{ x\in\mathbb{R}^n \ : \ d(x,a) < r \}$$

donde $d(x,y)$ es la distancia euclídea de $\mathbb{R}^n$:

Si $n = 1$, $$ d(x,a) = |x-a| $$
Si $n = 2$, $$ d(x,a) = \sqrt{(x_1-a_1)^2+(x_2-a_2)^2} $$
Si $n = 3$, $$ d(x,a) = \sqrt{(x_1-a_1)^2+(x_2-a_2)^2+(x_3-a_3)^2} $$

Representación:

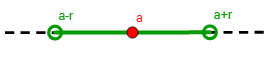
En la recta real ($n = 1$), la bola abierta $B_r(a)$ es el intervalo abierto $]a-r, a+r[$:
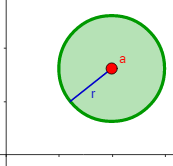
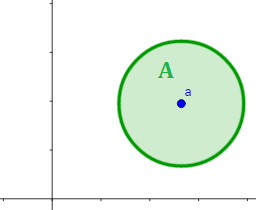
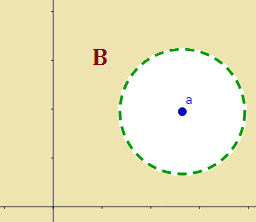
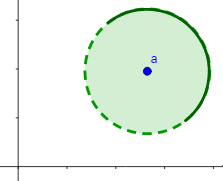
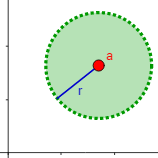
En el plano real ($n = 2$), la bola abierta $B_r(a)$ de centro $a =(a_1, a_2)$ es el círculo sin borde de centro $a$ y radio $r$:

$$ B_r(a)= \{ (x,y)\in \mathbb{R}^2 \ : \ (x-a_1)^2+(y-a_2)^2 < r^2 \} $$
En el espacio real ($n=3$), la bola abierta $B_r(a)$ de centro $a =(a_1, a_2,a_3)$ es el interior de la esfera de centro $a$ y radio $r$:

$$ B_r(a)= \{ (x_1,x_2,x_3)\in \mathbb{R}^3 \ : \ \sqrt{\sum_{1\leq i\leq 3}(x_i-a_i)^2}< r^2 \} $$

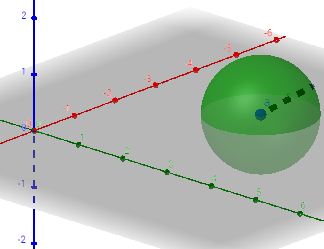
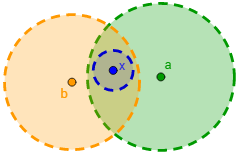
Nota: si cambiamos la distancia euclídea por otra métrica, las bolas tienen otras formas (ver espacio métrico y su topología).

2. Bola cerrada

Sean $a = (a_1, a_2, ...,a_n)\in \mathbb{R}^n$ y $r> 0$. Llamamos bola cerrada de centro $a$ y radio $r$ al conjunto

$$ \overline{B_r(a)} := \{ x\in\mathbb{R}^n \ : \ d(x,a) \leq r \}$$

La diferencia entre la bola abierta y la cerrada es que la cerrada incluye el borde y la abierta no.

Por ejemplo, una bola cerrada del plano es

$$ \overline{B_r(a)}= \{ (x,y)\in \mathbb{R}^2 \ : \ (x-a_1)^2+(y-a_2)^2 \leq r^2 \} $$

bolas abiertas, bolas cerradas, conjunto abierto, conjunto cerrado, topología usual

Es fácil ver que $B_r (a) \subset \overline{B_r(a)}$.

3. Conjunto abierto

Un subconjunto $A \subseteq \mathbb{R}^n$ es abierto si

$$ \forall x\in A,\ \exists B_x,\ x \in B_x \subseteq A $$

siendo $B_x$ una bola abierta que contiene a $x$.

Es decir, $A$ es un conjunto abierto si para cualquier punto $x\in A$ existe una bola abierta $B_x$ contenida en $A$ a la que $x$ pertenece. Observad que un abierto $A$ puede expresarse como unión de bolas abiertas:

$$ A = \bigcup_{x\in A} B_x $$

Nota: el conjunto vacío y el conjunto total ($\mathbb{R}^n$) son abiertos en todas las topologías (por definición).

Ejemplos y propiedades:

Toda bola abierta $B_r(a)$ es un conjunto abierto.

Para cada punto $x$ del conjunto $A = B_r(a)$, el punto $x$ está en la bola $A$ contenida en $A$.
El cuadrado sin borde $I^2 =(0,1) \times (0,1)$ es un conjunto abierto del plano real:

Para cualquier punto $x\in I^2$ podemos encontrar una bola $B_x$ que contiene a $x$ y contenida en $I^2$.
Las bolas cerradas $\overline{B_r(x)}$ no son conjuntos abiertos.

Dado un punto $a$ del borde de la bola, es decir, un punto $a$ cumpliendo $d(x,a) = r$, no existe ninguna bola abierta que contenga al punto $a$ y que esté contenida en la bola cerrada.
La unión de abiertos es un abierto.

Caso de la unión finita:

Supongamos que se trata de la unión de dos abiertos $A_1$ y $A_2$.

Sea $x$ un punto de esta unión, entonces es un punto de $A_1$ o de $A_2$.

Supongamos, sin pérdida de generalidad, que $x$ está en $A_1$. Como $A_1$ es un abierto, contiene una bola abierta $B_x$ que contiene a $x$. Entonces, la bola $B_x$ también está contenida en la unión $A_1 \cup A_2$:

$$ x\in B_x\subseteq A \subseteq A\cup B $$
La intersección finita de bolas abiertas es un abierto.

Supongamos que tenemos dos bolas abiertas $A_1$ y $A_2$ y que $x$ es un punto de la intersección $C = A \cap B$.

Sean $r_1$ y $r_2$ los radios de las bolas abiertas $A_1$ y $A_2$, respectivamente. Y sean $a_1$ y $a_2$ sus respectivos centros.

Como $x$ está en $C$, está en $A_1$ y en $A_2$. Por tanto, la distancia de $x$ a los centros de las bolas es menor que $r_1$ y $r_2$.

Sean

$$ k_1 = r_1 - d(x,a) $$

$$ k_2 = r_2 - d(x,b) $$

$$ \alpha = \min \left\lbrace \frac{k_1}{2}, \frac{k_2}{2}\right\rbrace $$

Entonces, la bola de centro $x$ y de radio $\alpha$ está contenida estrictamente en las bolas $A_1$ y $A_2$ y, por tanto, en su intersección $C$:

$$ x \in B_\alpha (x) \subset A_1 \cap A_2$$

En la imagen, el disco rojo es la bola $A_1$ y el disco azul es la bola $A_2$. El segmento rojo mide $k_1$ y el segmento azul mide $k_2$. La bola verde tiene radio $\alpha$.
La intersección finita de abiertos es un abierto.

Es consecuencia de que la intersección finita de bolas abiertas sea un abierto.

4. Conjunto cerrado

Un conjunto $A \subseteq \mathbb{R}^n$ es cerrado si su complementario $B = \mathbb{R}^n-A$ es un conjunto abierto.

$$B= \mathbb{R}^n - A := \{ x\in\mathbb{R}^n\ : \ x\not \in A \} $$

Ejemplos y propiedades:

Toda bola cerrada es un conjunto cerrado.

Representación de una bola cerrada del plano real:

Representación del complementario de la bola cerrada:
Cualquier punto es un conjunto cerrado.
La circunferencia $S_1$ del plano

$$ S^1 = \{(x,y)\in\mathbb{R}^2\ : \ x^2+y^2 = 1 \}$$

es un conjunto cerrado.

Dado un punto $x$ de la circunferencia, no existe ninguna bola abierta que lo contenga y que esté contenida en la circunferencia.
Un conjunto puede ser no abierto y no cerrado.
Un conjunto puede ser abierto y cerrado.

En la topología usual, los únicos conjuntos que son abiertos y cerrados son el conjunto vacío y el conjunto total $\mathbb{R}^n$.

En general, en los espacios conexos, los únicos conjuntos abiertos y cerrados son el vacío y el espacio total.
La unión finita de cerrados es un cerrado.

Sean $A_1$ y $A_2$ dos conjuntos cerrados y sea $C$ su unión: $C = A_1 \cup A_2$.

Los complementarios de $A_1$ y $A_2$ son

$$X_1 = \mathbb{R}^n -A_1 $$

$$X_2 = \mathbb{R}^n -A_2 $$

Son conjuntos abiertos porque $A_1$ y $A_2$ son cerrados.

Por tanto, su intersección $ Z = X_1 \cap X_2$ también es un abierto (intersección finita de abiertos).

Por las leyes de De Morgan, $Z$ es el complementario de $C$ (la intersección de los complementarios es el complementario de la unión).

Como $Z$ es el complementario de $C$ y es abierto, entonces $C$ es cerrado.
La intersección de cerrados es un cerrado.

Caso de intersección finita:

Sean $A$ y $B$ dos cerrados, para probar que su intersección es cerrada hay que probar que su complementario es abierto.

Por De Morgan, el complementario de la intersección de $A$ y $B$ es la unión de los complementarios de $A$ y de $B$. Pero como los complementarios de $A$ y de $B$ son abiertos, su unión también lo es.

Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.