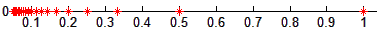Espacio y topológico y base de abiertos
En esta página definimos el concepto de espacio topológico, el de base de topología (o de abiertos) y proporcionamos algunos ejemplos de espacios topológicos.
Contenido de esta página:
- Espacio topológico
- Base de una topología
- Topología trivial
- Topología discreta
- Topología usual de \(\mathbb{R}\)
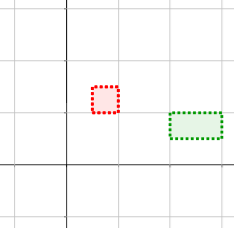
- Topología usual de \(\mathbb{R}^2\)
- Topología de Sorgenfrey
Páginas relacionadas
Otras páginas:
1. Espacio topológico
Sea \(X\) un conjunto y sea \(\mathcal{T}\) una familia (llamada topología sobre \(X\)) de subconjuntos de \(X\) (llamados abiertos) cumpliendo
- El conjunto vacío y el conjunto \(X\) son abiertos: $$\emptyset \in \mathcal{T}, X\in \mathcal{T} $$
- La unión de abiertos es un abierto: $$ \bigcup _{A_i \in I\subseteq \mathcal{T}} A_i \in \mathcal{T} $$
- La intersección finita de abiertos es un abierto: $$ \forall A,B \in \mathcal{T},\ A\cap B \in \mathcal{T} $$
Entonces, se dice que \(\mathcal{T}\) define una topología sobre \(X\), o que el par \((X,\mathcal{T})\) es un espacio topológico.
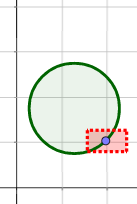
A los conjuntos complementarios de los abiertos se les denomina cerrados. Es decir, \(A\) es cerrado si \(X-A\) es abierto.
Otras definiciones importantes:
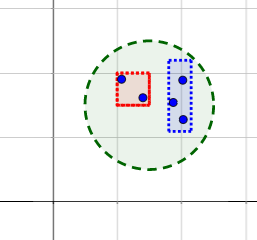
- En un espacio topologico \((X,\mathcal{T})\), se dice que \(U\subseteq X\) es un entorno de un punto \(x\in X\) si existe un abierto \(A\in\mathcal{T}\) tal que \(x\in A\subseteq U\).
- Denotamos por \(\xi (x)\) al conjunto de entornos de \(x\in X\).
Observad que un abierto \(A\in\mathcal{T}\) es un entorno de todo \(x\in A\).