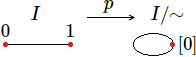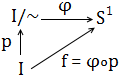Espacio topológico cociente

En esta página definimos el espacio topológico cociente definido por una relación de equivalencia y damos algunos ejemplos (circunferencia, cinta de Möbius y toro). En el último apartado demostramos otras dos proposiciones que utilizamos para construir los homeomorfismos de los ejemplos.

Contenido de esta página:

1. Relación de equivalencia
2. Clases y conjunto cociente
3. Topología cociente
4. Ejemplo 1: circunferencia
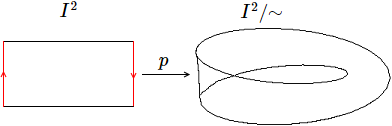
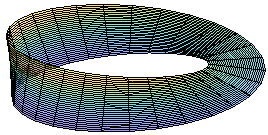
5. Ejemplo 2: cinta de Möbius
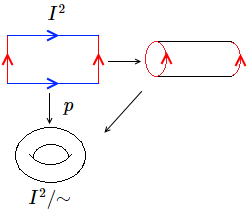
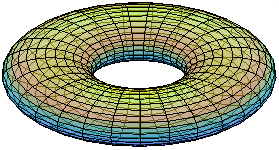
6. Ejemplo 3: toro
7. Otros resultados teóricos

Una relación de equivalencia \( \sim \) sobre el conjunto \(X\) es una relación binaria sobre \(X\) cumpliendo las siguientes propiedades:

• Reflexividad: \(\forall x\in X,\ x\sim x\)
• Simetría: \(\forall x,y\in X\), \(\ x\sim y \rightarrow y\sim x \)
• Transitividad: : \(\forall x,y,z\in X\), \(\ x\sim y \land y\sim x \rightarrow x\sim z\)

Dado \(x\in X\), se define la clase de equivalencia de \(x\) como

$$ [x]:= \{y\in X : x\sim y\} $$

El conjunto de todas las clases de equivalencia que define \(\sim \) sobre \(X\) se denota por \(X/{\sim}\) y se denomina conjunto cociente:

$$ X/{\sim} := \{[x]: x\in X\} $$

Llamamos proyección a la aplicación de \(X\) en el conjunto cociente \(X/{\sim}\) dada por

$$ \begin{align*} p \colon & X \to X/{\sim} \\ & x \mapsto [x] \end{align*} $$

Sean \((X,\mathcal{T})\) un espacio topológico, \(\sim\) una relación de equivalencia sobre \(X\) y \(p\colon X \to X/{\sim}\) su proyección. Llamamos espacio topológico cociente a \((X/{\sim},\mathcal{T}_\sim)\), siendo \(\mathcal{T}_\sim\) la familia de subconjuntos \(A\subseteq X/{\sim}\) cuya antiimagen \(p^{-1}(A)\) es un abierto de \(\mathcal{T}\).

Definimos sobre \(I = [0,1]\) (segmento de longitud 1) la relación de equivalencia \(0\sim 1\). Es decir, cada punto está relacionado consigo mismo excepto 0 y 1, que también están relacionados entre sí.

Las clases de equivalencia de esta relación son

• \([x] = \{x\}, \forall x\neq 0,1\)
• \([0] = [1] = \{ 0,1\}\)

Lo que hace la relación es identificar los dos extremos del segmento, así que, podemos imaginar que su conjunto cociente es una circunferencia:

Ahora vamos a ver, formalmente, que el conjunto cociente \(I/{\sim}\) es homeomorfo a

$$ S^1 := \{(x,y)\in \mathbb{R}^2 : x^2+y^2 = 1\} $$

Sea \(f\colon I\to S^1\) definida por \(f(t) = (cos(2\pi t), sin(2 \pi t))\). Esta aplicación es continua, pero no es biyectiva porque \(f(0)=f(1)=(1,0)\) (el punto \((1,0)\) tiene dos antiimágenes).

Consideremos el siguiente diagrama:

donde \(p\) es la proyección.

Como \(p(0)=p(1)\), la aplicación \(f\) induce la biyección \(\varphi \colon I/{\sim}\to S^{1}\). Observad que el punto \((1,0)\) tiene una única antiimagen y es \([0]=[1]\).

Como \(f\) y \(p\) son continuas, \(\varphi\) es continua (Proposición 3).

Como \(\varphi\) es una biyección continua entre compactos, es cerrada (Proposición 4).

Como \(\varphi\) es una biyección continua y cerrada, es un homeomorfismo (Proposición 5).

Por tanto, el espacio \(I/{\sim}\) es homeomorfo a \(S^1\).

Definimos sobre \(I^2 = [0,1]\times [0,1]\) (cuadrado de lado 1) la relación de equivalencia dada por \( (0,y)\sim (1,1-y)\), \(\forall y\in I \). Es decir, se identifican los lados laterales, pero en sentido contrario:

El espacio topológico \(I^2/{\sim}\) es homeomorfo a la cinta de Möbius, que puede ser definida como

$$\{ f(u,v) : u\in [0,2\pi], v\in I\}$$

siendo \( f(u,v)=(x(u,v),y(u,v),z(u,v)) \) la función dada por

$$ x(u,v) = \left(1+\frac{v}{2}·cos\left(\frac{u}{2}\right)\right)·cos(u)$$

$$ y(u,v) = \left(1+\frac{v}{2}·cos\left(\frac{u}{2}\right)\right)·sin(u)$$

$$ z(u,v) = \frac{v}{2}·sin\left(\frac{u}{2}\right)$$

Representaciones:

El homeomorfismo puede hallarse modificando ligaramente la función \(f\) y razonando como en el ejemplo anterior.

Definimos sobre \(I^2 = [0,1]\times [0,1]\) (cuadrado de lado 1) la relación de equivalencia dada por

• \( (x,0)\sim (x,1), \forall x\in I \)
• \( (0,y)\sim (1,y), \forall y\in I \)

Es decir, esta relación identifica el lado inferior con el superior y el lado izquierdo con el derecho:

Este espacio topológico es homeomorfo a un toro, que puede ser definido por

$$\{ f(u,v) : u,v \in [0,2\pi )\}$$

siendo \( f(u,v) = (x(u,v),y(u,v),z(u,v)) \) la función dada por

$$ x(u,v) = cos(u)(2+cos(v)) $$

$$ y(u,v) = sin(u)(2+cos(v)) $$

$$ z(u,v) = sin(v) $$

Representaciones:

Recordamos que en \( \mathbb{R}^n \) un conjunto es compacto si, y sólo si, es cerrado y acotado. También, que los subespacios de los espacios de Hausdorff también son de Hausdorff.

---